
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ДОДАТКИ 1 страница. Основні формули для обчислення статистичних показників
|
|
|
|
Додаток А
Основні формули для обчислення статистичних показників
| № формули | Назва показника | Формула | Умовні позначення |
| Тема 3. Зведення і групування статистичних даних | |||
| Кількість груп | 
| n – кількість груп; N – обсяг сукупності | |
| Величина інтервалу | 
| і – величина інтервалу;
 – максимальне значення ознаки; – максимальне значення ознаки;
 – мінімальне значення ознаки; – мінімальне значення ознаки;
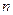 – кількість груп – кількість груп
| |
| Тема 4. Узагальнюючі статистичні показники | |||
| Відносна величина планового завдання | 
| 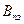 – відносна величина планового завдання; – відносна величина планового завдання;
 – плановий рівень показника, що вивчається у поточному періоді (або план на майбутній період); – плановий рівень показника, що вивчається у поточному періоді (або план на майбутній період);
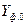 – фактичний рівень показника за попередній період (або фактичний за звітний період). – фактичний рівень показника за попередній період (або фактичний за звітний період).
| |
| Відносна величина виконання плану | 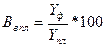
| Вв.пл – відносна величина виконання плану; Yф – фактичний рівень показника за досліджуваний період; Yпл – плановий рівень показника за цей же період. | |
| Відносна величина динаміки | 
| Вд – відносна величина динаміки; Yф1 – фактичний рівень показника за звітний період; Yф0 – фактичний рівень показника за попередній період, або за період, взятий за базу порівняння. |
Продовження додатку А
| Відносна величина структури | 
| Вст – відносна величина структури;
 – і -та частина сукупності; – і -та частина сукупності;
 – загальний обсяг сукупності – загальний обсяг сукупності
| |
| Відносна величина координації | 
| Вкоор – відносна величина координації; fi – і -та частина сукупності; fj – j -та частина сукупності; (і≠ j) | |
| Відносна величина інтенсивності | 
| Вінтенс – відносна величина інтенсивності; а – обсяг певного явища; В – обсяг середовища, у якому це явище поширене. | |
| Відносна величина порівняння | 
| Впорів – відносна величина порівняння;
 – певна характеристика об’єкта А (або території); – певна характеристика об’єкта А (або території);
 – така ж характеристика об’єкта В (або території). – така ж характеристика об’єкта В (або території).
| |
| Середня арифметична проста | 
| хі – варіанти, тобто індивідуальні значення ознаки; n – число варіант, тобто кількість одиниць сукупності. | |
| Середня арифметична зважена | 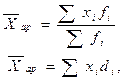
| хі – варіанти, тобто окремі значення ознаки; fi - частота,що відповідає варіанті; di - частка i - ї групи. | |
| Середня хронологічна | 
| х – варіанти, тобто окремі значення ознаки; n – число моментів. | |
| Середня геометрична проста | 
| xі – відносні величини динаміки, виражені кратним відношенням j -го значення показника до попереднього; n - число осереднюваних величин; | |
| Середня геометрична зважена | 
|  , ,  … …  - середні коефіцієнти динаміки за окремі періоди; - середні коефіцієнти динаміки за окремі періоди;
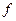 - тривалість окремих періодів (ваги). - тривалість окремих періодів (ваги).
|
Продовження додатку А
| Середня гармонічнапроста | 
| х – варіанти (окремі значення ознаки); n – число варіант. | |
| Середня гармонічна зважена | 
| х – окремі значення ознаки; w – обсяг явища. | |
| Середня квадратична проста | 
| х – варіанти (окремі значення ознаки); n – число варіант. | |
| Середня квадратична зважена | 
| хі – варіанти (окремі значення ознаки); fi - частота,що відповідає варіанті. | |
| Середнє значення інтервалу | 
| xmin – мінімальне значення інтервалу; xmax – максимальне значення інтервалу. | |
| Тема 5. Аналіз рядів розподілу | |||
| Щільність розподілу (щільність частоти) | 
| gj – щільність розподілу; fj - частота j-го інтервалу; іj – розмір j-го інтервалу. | |
| Відносна щільність розподілу (щільність частки) | 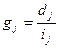
| gj – щільність розподілу; dj – частка j-го інтервалу; іj – розмір j-го інтервалу. | |
| Модальне значення ознаки в межах інтервалу (Мо) | 
| x0 – нижня межа модального інтервалу. i – величина інтервалу. f2 – частота модального інтервалу, f1 – частота інтервалу, що передує модальному; f3 – частота позамодального інтервалу (того, що йде після модального інтервалу) | |
| Медіанне значення ознаки (Ме) | 
| x0 – це нижня межа медіанного інтервалу; i – величина інтервалу; Sm-1 – сума накопичених частот до медіанного інтервалу; fm – частота медіанного інтервалу. |
Продовження додатку А
| Розмах варіації (R) | R = xmax - xmin | xmin – мінімальне значення ознаки; xmax – максимальне значення ознаки. | |
Середнє лінійне відхилення (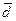 ) )
| 
| х – окремі значення ознаки;
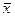 – середнє значення ознаки;
п – кількість елементів сукупності. – середнє значення ознаки;
п – кількість елементів сукупності.
| |
Зважене середнє лінійне відхилення (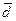 ) )
| 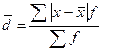
| х – окремі значення ознаки;
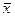 – середнє значення ознаки;
f – частоти значень ознаки. – середнє значення ознаки;
f – частоти значень ознаки.
| |
| Дисперсія (проста) | 
| х – значення ознаки;
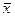 – середнє значення ознаки;
п – кількість елементів сукупності. – середнє значення ознаки;
п – кількість елементів сукупності.
| |
| Дисперсія (зважена) | 
| х – значення ознаки;
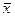 – середнє значення ознаки;
f – частоти значень ознаки. – середнє значення ознаки;
f – частоти значень ознаки.
| |
| Середнє квадратичне відхилення (просте) | 
| х – значення ознаки;
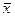 – середнє значення ознаки;
п – кількість елементів сукупності. – середнє значення ознаки;
п – кількість елементів сукупності.
| |
| Середнє квадратичне відхилення (зважене) | 
| х – значення ознаки;
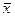 – середнє значення ознаки;
f – частоти значень ознаки. – середнє значення ознаки;
f – частоти значень ознаки.
| |
| Коефіцієнт варіації (лінійний) | 
| 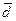 – середнє лінійне відхилення; – середнє лінійне відхилення;
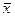 – середнє значення досліджуваної ознаки. – середнє значення досліджуваної ознаки.
| |
| Коефіцієнт варіації (квадратичний) | 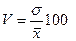
|  – середнє квадратичне відхилення; – середнє квадратичне відхилення;
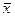 – середнє значення досліджуваної ознаки. – середнє значення досліджуваної ознаки.
| |
| Групова (часткова) дисперсія | 
| σі2 – групова (часткова) дисперсія;
уі – окремі значення ознаки всередині і -тої групи;
 – середнє значення ознаки в межах і-тої групи;
fі – частота значень ознаки всередині і- тої групи. – середнє значення ознаки в межах і-тої групи;
fі – частота значень ознаки всередині і- тої групи.
|
Продовження додатку А
| Середня з групових (часткових) дисперсій | 
|  - середня з групових (часткових) дисперсій;
σі2 – групова (часткова) дисперсія і -тої групи;
fі – частота значень ознаки всередині і- тої групи. - середня з групових (часткових) дисперсій;
σі2 – групова (часткова) дисперсія і -тої групи;
fі – частота значень ознаки всередині і- тої групи.
| |
| Міжгрупова дисперсія | 
| σм2 – міжгрупова дисперсія;
 – середнє значення ознаки в межах і-тої групи; – середнє значення ознаки в межах і-тої групи;
 – середнє значення ознаки по всій сукупності;
fі – частота значень ознаки всередині і- тої групи;
∑ f – сума всіх частот, або обсяг сукупності. – середнє значення ознаки по всій сукупності;
fі – частота значень ознаки всередині і- тої групи;
∑ f – сума всіх частот, або обсяг сукупності.
| |
| Тема 6. Аналіз концентрації, диференціації та подібності розподілів | |||
| Момент розподілу | 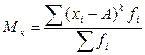
| Мк – момент к- го порядку; хі – варіанти ряду розподілу; А – постійна величина, від якої визначаються відхилення; к – показник ступеня, що визначає порядок моменту; fi – частоти ряду. | |
| Початковий момент розподілу | 
| хік – варіанти ряду розподілу к -го ступеня; fi – частоти ряду. | |
| Центральний момент розподілу | 
| хі – варіанти ряду розподілу;
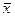 – середнє значення ознаки в ряду розподілу;
fi – частоти ряду. – середнє значення ознаки в ряду розподілу;
fi – частоти ряду.
| |
| Нормований (стандартизований) момент розподілу | 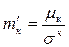
| μк - центральний момент к -го порядку; σк – середнє квадратичне відхилення в к -му ступені. | |
| Відносний показник асиметрії | 
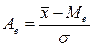
| 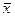 – середнє значення ознаки в ряду розподілу;
М0 – модальне значення ознаки;
Ме – медіанне значення ознаки; – середнє значення ознаки в ряду розподілу;
М0 – модальне значення ознаки;
Ме – медіанне значення ознаки;
 – середнє квадратичне відхилення – середнє квадратичне відхилення
|
Продовження додатку А
| Коефіцієнт асиметрії (А) | 

| μ3 - центральний момент третього порядку;
σ3 – середнє квадратичне відхилення у третьому ступені;
хі – окремі значення ознаки;
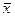 – середнє значення ознаки;
fі – частоти значень ознаки. – середнє значення ознаки;
fі – частоти значень ознаки.
| |
| Коефіцієнт ексцесу (Е) | 
| μ4 – центральний нормований момент четвертого порядку;
σ – середнє квадратичне відхилення;
хі – окремі значення ознаки;
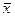 – середнє значення ознаки;
fі – частоти значень ознаки. – середнє значення ознаки;
fі – частоти значень ознаки.
| |
| Коефіцієнт концентрації (К) | 
| dj – частки розподілу елементів сукупності; Dj – частки розподілу значень ознаки. | |
| Коефіцієнт локалізації (Lj) | 
| dj – частки розподілу елементів сукупності; Dj – частки розподілу значень ознаки. | |
| Коефіцієнт подібності (схожості) розподілів (P) | 
|  - модуль відхилення часток аналізованих сукупностей. - модуль відхилення часток аналізованих сукупностей.
| |
| Лінійний коефіцієнт структурних зрушень (ld) | 
| dj1, dj0 – частки, відповідно, поточного та базисного періодів; m – кількість складових сукупності. | |
| Квадратичний коефіцієнт структурних зрушень (σd) | 
| dj1, dj0 – частки, відповідно, поточного та базисного періодів; m – кількість складових сукупності. | |
| Тема 7. Статистичні методи вимірювання взаємозв’язків | |||
| Коефіцієнт Фехнера (Кф) | 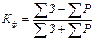
| ∑З – сума знаків відхилень [  та та  ], які збігаються в обох рядах;
∑Р – сума знаків відхилень, які не збігаються (розбіг знаків). ], які збігаються в обох рядах;
∑Р – сума знаків відхилень, які не збігаються (розбіг знаків).
|
Продовження додатку А
Коефіцієнт кореляції рангів Спірмена (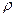 ) )
| 

| d – різниця між рангами в порівняльних рядах; п – число рангів; Rx – ранг факторної ознаки; Ry – ранг результативної ознаки. | |
| Коефіцієнт кореляції рангів Кендела (τ) | 
| S1 – число рангів, які перевищують номер рангу за результативною ознакою; S2 – число рангів, менших за ранг результативної ознаки у подальших записах; п – число рангів. | |
| Коефіцієнт детермінації (η2) | 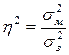
| 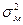 – міжгрупова дисперсія; – міжгрупова дисперсія;
 – загальна дисперсія – загальна дисперсія
| |
| Емпіричне кореляційне відношення (η) | 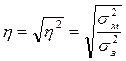
| η2 – коефіцієнт детермінації (емпіричний);
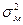 – міжгрупова дисперсія; – міжгрупова дисперсія;
 – загальна дисперсія – загальна дисперсія
| |
| Критерій Фішера (F - критерій) | 

| σм2 – міжгрупова дисперсія;
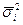 - середня з групових (залишкова) дисперсія;
k1, k2 – ступені вільності для великої i малої дисперсій;
η2 – коефіцієнт детермінації. - середня з групових (залишкова) дисперсія;
k1, k2 – ступені вільності для великої i малої дисперсій;
η2 – коефіцієнт детермінації.
| |
| Ступені вільності | 
| т – число груп; п – кількість елементів досліджуваної сукупності | |
| Критерій Стьюдента (t - критерій) | 

| 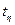 – критерій Стьюдента; – критерій Стьюдента; 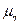 – середня похибка кореляційного відношення; η2 – коефіцієнт детермінації; п – кількість елементів досліджуваної сукупності. – середня похибка кореляційного відношення; η2 – коефіцієнт детермінації; п – кількість елементів досліджуваної сукупності.
| |
| Метод найменших квадратів для лінійної функції | 
| п – кількість елементів досліджуваної сукупності; х – значення факторної ознаки; а1, а0 – параметри рівняння. | |
| Параметри рівняння лінійної функції | 

| 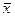 – середнє значення факторної ознаки; – середнє значення факторної ознаки;
 – середнє значення результативної ознаки;
а1, а0 – параметри рівняння. – середнє значення результативної ознаки;
а1, а0 – параметри рівняння.
|
Продовження додатку А
| Коефіцієнт еластичності кожного елемента сукупності (ε) | 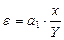

| х – фактичне значення факторної ознаки;
Y – розрахункове значення результативної ознаки, яке відповідає факторній ознаці х;
 – середнє значення результативної ознаки. – середнє значення результативної ознаки.
| |
| Коефіцієнт еластичності для всіх елементів сукупності (ε) | 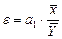
| а1 – параметр рівняння;
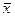 – середнє значення факторної ознаки; – середнє значення факторної ознаки;
 – середнє значення результативної ознаки. – середнє значення результативної ознаки.
| |
| Коефіцієнт детермінації для парної регресії (R2) | 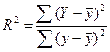
| Y – теоретичні (розрахункові) значення результативної ознаки для кожного значення «х»;
y – фактичні значення результативної ознаки для кожного значення «х»;
 – середнє значення результативної ознаки. – середнє значення результативної ознаки.
| |
| Коефіцієнт кореляції (R) | 
| R2 – коефіцієнт детермінації. | |
| Лінійний коефіцієнт кореляції (r) | 

|  - середнє квадратичне відхилення факторної ознаки; - середнє квадратичне відхилення факторної ознаки;
 - середнє квадратичне відхилення результативної ознаки;
а1 – параметр рівняння;
п – кількість елементів. - середнє квадратичне відхилення результативної ознаки;
а1 – параметр рівняння;
п – кількість елементів.
| |
| Часткові коефіцієнти еластичності (εі) | 
| аі – коефіцієнт регресії при і-му факторі;
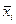 - середнє значення і-го фактора; - середнє значення і-го фактора;
 - середнє значення результативного показника. - середнє значення результативного показника.
| |
| Часткові β- коефіцієнти | 
| аі – коефіцієнт регресії при і-му факторі;
 - середнє квадратичне відхилення і-го фактора; - середнє квадратичне відхилення і-го фактора;
 - середнє квадратичне відхилення результативної ознаки. - середнє квадратичне відхилення результативної ознаки.
|
Продовження додатку А
| Коефіцієнт множинної (сукупної) детермінації (R2) | 
|  - дисперсія результативного показника, обчислена за рівнянням регресії; - дисперсія результативного показника, обчислена за рівнянням регресії;
 - загальна дисперсія результативного показника;
Y – теоретичні значення результативного показника, обчислені за рівнянням регресії;
y – фактичні значення результативного показника; - загальна дисперсія результативного показника;
Y – теоретичні значення результативного показника, обчислені за рівнянням регресії;
y – фактичні значення результативного показника;
 – середнє значення результативного показника. – середнє значення результативного показника.
| |
| Множинний коефіцієнт кореляції (R) | 
|  - дисперсія результативного показника, обчислена за рівнянням регресії; - дисперсія результативного показника, обчислена за рівнянням регресії;
 - загальна дисперсія результативного показника. - загальна дисперсія результативного показника.
| |
| Коефіцієнт взаємного сполучення К. Пірсона (СП) | 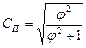
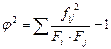
| φ2 – сума квадратів частот кожного рядка таблиці, поділена на суму частот по стовпчиках і на суму частот рядка, без одиниці; fij – значення частоти, що є на перетині і -ої строки та j -го стовпчика таблиці взаємної спряженості; Fi – сума частот за і -тою строкою таблиці; Fj – сума частот за j -тим стовпчиком таблиці. | |
| Коефіцієнт взаємного сполучення А. Чупрова (СЧ) | 
| φ2 – сума квадратів частот кожного рядка таблиці, поділена на суму частот по стовпчиках і на суму частот рядка, без одиниці; К1 – кількість груп у стовпчиках таблиці; К2 – кількість груп у рядках таблиці. | |
| Статистичний критерій χ2 («хі»-квадрат) | 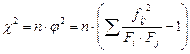
| п – обсяг досліджуваної сукупності. | |
| Коефіцієнт асоціації Юла (Q) | 
| a, b, c, d – позначення клітинок таблиці взаємної спряженості. |
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 744; Нарушение авторских прав?; Мы поможем в написании вашей работы!