Зразки розв’язування задач. Контрольні запитання

РЯДИ

Контрольні запитання

1 Яке рівняння називають диференціальним?

2 Що таке порядок диференціального рівняння?

3 Як формулюється означення загального розв’язку, частинного розв’язку, загального інтеграла диференціального рівняння?

4 У чому полягає задача Коші для диференціального рівняння І порядку?

5 Яке диференціальне рівняння І порядку називається рівнянням із відокремлюваними змінними, як воно розв’язується?

6 Яке диференціальне рівняння І порядку називається однорідним, як воно зводиться до рівняння з відокремлюваними змінними?

7 Яке диференціальне рівняння називається лінійним, метод його розв’язання?

8 Як записується загальний розв’язок лінійних однорідних диференціальних рівнянь ІІ порядку із сталими коефіцієнтами в різних випадках?

9 У чому полягає метод невизначених коефіцієнтів знаходження частинних розв’язків лінійного неоднорідного диференціального рівняння ІІ порядку?

Література: [2] – ст. 374-398; [3] – ст. 301-309; [4] – ст. 493-527.

Числовий ряд

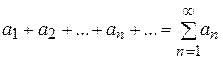, (7.1)

називається збіжним, якщо існує границя частинних сум 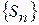. Число 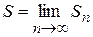називається сумою ряда. Якщо ж границя частинних сум не існує, то ряд 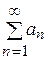– розбіжний.

Необхідна ознака збіжності ряду: Якщо ряд 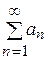збіжний, то його загальний член прямує до нуля при , .

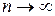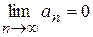Достатні ознаки збіжності знакододатніх рядів:

а) Ознака порівняння.

Теорема 1. Нехай задано два знакододатні ряди 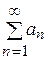, 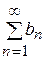і 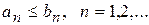Якщо ряд 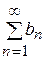– збіжний, то ряд 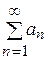також збіжний. Якщо ряд 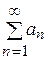– розбіжний, то ряд 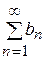теж розбіжний.

Теорема 2. Нехай задано два знакододатні ряди 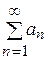, 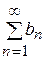та 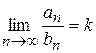(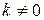, тобто існує границя відношення), то ці ряди одночасно збіжні або розбіжні.

Серед числових рядів важливу роль відіграють:

1)

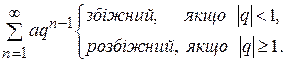
2) 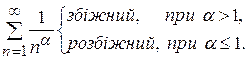– це узагальнений гармонічний ряд, при 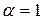ряд називається гармонічним, він розбіжний (це можна довести).

Приклад 6. Дослідити збіжність числового ряду .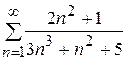

Розв’язання.

Застосуємо граничну ознаку порівняння. Для порівняння візьмемо ряд – гармонічний, розбіжний.

Шукаємо границю відношення:

.

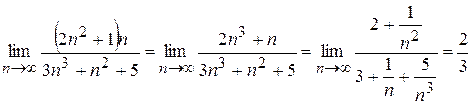Так як одержана границя рівна 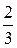, то ряди ведуть себе однаково, тобто ряд 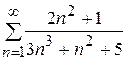теж розбіжний.

б) Ознака Д’Аламбера.

Теорема 3. Якщо в знакододатньому ряду 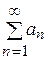, існує границя 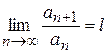, то

1. ряд збіжний, якщо ;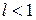

2. ряд розбіжний, якщо ;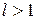

3. при 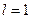потрібно дослідити за іншою ознакою.

Приклад 7. (Задача 4.3(а)) Дослідити збіжність числового ряду .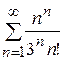

Розв’язання.

Скористаємося ознакою Д’Аламбера:

, ,

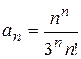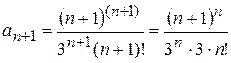отже 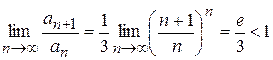– ряд збіжний.

в) Радикальна ознака Коші.

Теорема 4 Якщо в знакододатньому ряду 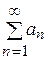, існує границя 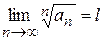, то

1. ряд збіжний, якщо ;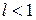

2. ряд розбіжний, якщо ;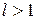

3. при 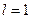потрібно дослідити за іншою ознакою.

Приклад 8. (Задача 4.3(б)) Дослідити збіжність числового ряду .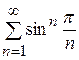

Розв’язання.

Скористаємося радикальною ознакою Коші: .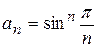

Отже, 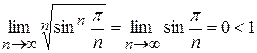– ряд збіжний.

г) Інтегральна ознака Коші.

Теорема 5. Нехай задано ряд 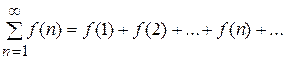, члени якого є значеннями неперервної, додатньої і монотонно спадної функції 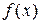на проміжку 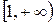. Тоді ряд 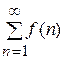збіжний, якщо збіжний невласний інтеграл 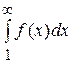, і цей ряд розбіжний, якщо розбіжний невласний інтеграл .

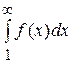Приклад 9. (Задача 4.3(в)) Дослідити збіжність числового ряду

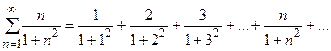
Розв’язання.

Скористаємося інтегральною ознакою Коші. Функція 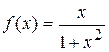на проміжку 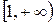є:

1) неперервна;

2) додатня;

3) знайдемо 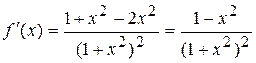при 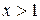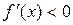, тобто функція спадає.

Розглянемо невласний інтеграл:

.

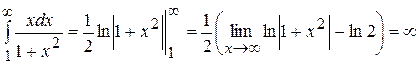Цей інтеграл розбіжний, тому і заданий ряд розбіжний.

Дата добавления: 2014-11-29