План уроку. 1.Рух без початкової швидкістю

1.Рух без початкової швидкістю

2.Рух із початковою швидкістю

3.Співвідношення між шляхом і швидкістю

1.Рух без початкової швидкістю

У випадку прямолінійного рівномірного руху тіла переміщен­ня, яке здійснює це тіло, обчислюється як площа прямокутника, що міститься під графіком модуля швидкості.

І в разі прямолінійного рівноприскореного руху переміщення (або шлях) можна обчислювати за тією ж формулою, що й площу фігури під графіком швидкості.

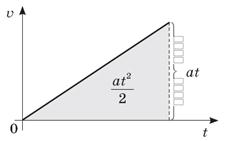
У випадку прямолінійного рівноприскореного руху без початко­вої швидкості залежність шляху l від часу руху t описується формулою:

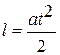
де a — модуль прискорення тіла.

Слід звернути увагу учнів на те, що в разі рівноприскореного руху без початкової швидкості шлях пропорційний квадрату часу руху.

2.Рух із початковою швидкістю

Якщо початкова швидкість тіла не дорівнює нулю, то фігура, обмежена графіком 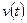і віссю 0 t, — трапеція, що складається з прямокутника площею v₀t і трикутника площею .

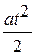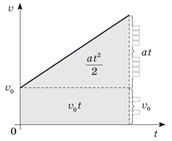Отже, шлях можна обчислити за формулою .

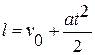Таким чином, якщо тіло рухається прямолінійно рівноприско­рено з початковою швидкістю v ₀ і прискоренням a, то залежність шляху l від часу руху t має вигляд:

,

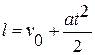якщо напрямок прискорення збігається з напрямком початкової швидкості, і вигляд:

,

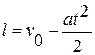якщо прискорення спрямоване протилежно напрямку початкової швидкості. Необхідно звернути увагу на те, що в першому ви­падку швидкість тіла збільшується, а в другому — зменшується.

Оскільки площа трапеції дорівнює півсумі основ і висоти, то 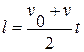. З іншого боку, 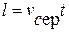. Звідси випливає, що середня швидкість у разі рівноприскореного руху дорівнює: .

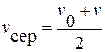3.Співвідношення між шляхом і швидкістю

З формул для шляху 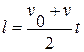і часу 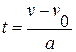дістаємо: 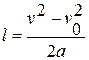. Якщо початкова швидкість дорівнює нулю, ця формула набуває вигляду: .

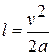Розв’язування задач

1. По прямому шосе зі швидкістю v₁ = 16 м/с рухається автобус. На відстані d = 60 м від шосе і s = 400 м від автобуса знаходиться людина. Людина може бігти зі швидкістю v₂ = 4 м/с. В якому напрямку він повинен бігти, щоб встигнути «перехопити» автобус, який до нього наближається? При якій найменшій швидкості людини v _2min це взагалі можливо? В якому направпрямі слід при цьому бігти?

2. Атомне ядро летить зі швидкістю v і розпадається на два однакові осколки. Визначте максимально можливий кут α між швидкістю ядра і швидкістю осколка, якщо відомо, що при розпаді спочиваючого ядра кожен з осколків набуває швидкість u.

3. Ліфт починає підніматися з прискоренням а =2,2 м/с². Коли його швидкість досягла v = 2,4 м/с, зі стелі кабіни ліфта почав падати болт. Чому дорівнюють час t падіння болта і переміщення болта при падінні щодо Землі? Висота кабіни ліфта Н = 2,5 м.

4. Потяг пройшов відстань між двома станціями s = 17 км зі середньою швидкістю vcp ~ 60 км/год. При цьому на розгін до початку руху і гальмування перед зупинкою він витратив у загальній складності t₁ = 4 хв, а решту часу рухався з постійною швидкістю v. Чому дорівнює ця швидкість?

Домашнє завдання:

1. Автобус рухається по прямому шосе зі швидкістю v₁. Людина може бігти з меншою швидкістю v ₂. Визначте геометричне місце точок, в яких може перебувати спочатку людина, щоб встигнути «перехопити» автобус.

2. Лижник з їхав з гори довжиною s₁ = 60 м за t= 15 с, а потім проїхав по горизонтальній ділянці ще s₂= 30 м до зупинки. Знайдіть швидкість v₁ лижника в кінці спуску і прискорення а₂ на горизонтальній ділянці. Побудуйте графік залежності швидкості від часу.

Тема уроку: Вільне падіння тіл. Прискорення вільного падіння. Рух тіла, кинутого вертикально вгору, горизонтально і під кутом до горизонту

Дата добавления: 2014-11-29