Then begin 1 страница

Begin

Begin

Begin

Begin

Begin

Begin

Begin

Begin

If f

Begin

Else

Begin

Begin

Repeat

Begin

Repeat

Begin

Begin

Begin

Begin

Begin

Begin

Begin

<команди тіла циклу>

end;

Рядок for … to … do ( англ. for – для, to – до, do – робити, виконувати ) називається рядком заголовку команди циклу з лічильником. Змінна в рядку заголовка команди циклу з лічильником, що стоїть перед знаком присвоювання, називається лічильником циклу.

Лічильник циклу, вираз1 і вираз2 мають набувати тільки цілих значень. Якщо тіло циклу складається лише з однієї команди, операторні дужки begin і end можна не ставити.

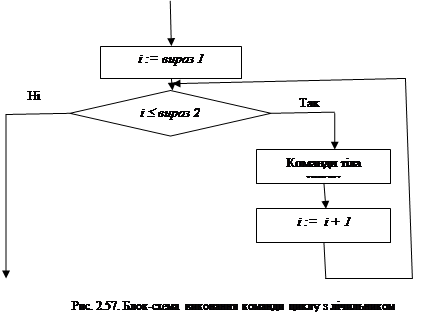Виконується команда циклу з лічильником так:

1. Надати лічильнику циклу значення виразу1.

2. Обчислити значення логічного виразу i £ вираз 2

3. Якщо значення лічильнику циклу не перевищує значення виразу2, то виконати команди тіла циклу і перейти до виконання команди 3, інакше виконати команду, наступну за командою циклу.

4. Збільшити значення лічильника циклу на 1.

5. Перейти до виконання команди 2.

Блок-схема виконання команди циклу з лічильником наведена на рис. 2.57 (і – лічильник циклу).

Для ілюстрації виконання команди циклу з лічильником розглянемо фрагмент програми, в якому обчислюється сума 1! + 2! + 3! +4! (нагадаємо, що n! = 1×2×3×...×n):

var a, s, i: Integer;

s:= 0; a:= 1;

For i:= 1 to 4 do

a:= a*i;

s:= s + a;

end;

Label1.Caption:= IntToStr (s);

end;

Функція IntToStr (англ. int eger to str ing– ціле в рядок) використовується для переведення цілого числа в його текстове представлення для виведення в напис.

Виконаємо цей фрагмент програми.

Команда	Результат виконання
s:= 0	s = 0
a:= 1	a = 1
i:= 1	i = 1
і <= 4	(1 <= 4) = true
a:= a*i	a = 1*1= 1
s:= s + a	s = 0 + 1 = 1
i:= i + 1	i = 2
і <= 4	(2 <= 4) = true
a:= a*i	a = 1*2= 2
s:= s + a	s = 1 + 2 = 3
i:= i + 1	i = 3
і <= 4	(3 <= 4)= true
a:= a*i	a = 2*3= 6
s:= s + a	s = 3 + 6 = 9
i:= i + 1	i = 4
і <= 4	(4 <= 4) =true
a:= a*i	a = 6*4= 24
s:= s + a	s = 9 + 24 = 33
i:= i + 1	i = 5
і <= 4	(5 <= 4) = false
Label1.Caption:= IntToStr (s)	Label1.Caption = 33

Звертаємо вашу увагу:

1. Після закінчення виконання команди циклу з лічильником лічильник циклу має значення на 1 більше значення виразу2, і це значення, при необхідності, можна використовувати в наступних командах.

2. Існує різновид команди циклу з лічильником, який змінюється в зворотному порядку:

For <ім′я змінної>:= <вираз1> downto <вираз2> do

<команди тіла циклу>

end;

(англ. down – униз), який відрізняється від попереднього лише тим, що після кожного виконання команд тіла циклу значення лічильника циклу не збільшується на 1, а зменшується на 1.

Команди циклу з передумовою і циклу з післяумовою в Delphi

Якщо кількість повторень команд тіла циклу до початку виконання команди циклу невідома, потрібно використовувати команду циклу з передумовою або команду циклу з післяумовою.

Загальний вигляд команди циклу з передумовою такий:

while <логічний вираз> do

<команди тіла циклу>

end;

( англ. while – поки). Якщо тіло циклу складається лише з однієї команди, операторні дужки begin і end можна не ставити.

Виконується команда циклу з передумовою так:

6. Обчислити значення логічного виразу.

7. Якщо це значення true, то виконати команди тіла циклу і перейти до команди 1, а якщо false, то виконати команду, наступну за командою циклу.

Для ілюстрації виконання команди циклу з передумовою розглянемо фрагмент програми для розв’язування наступної задачі.

Задача 2. Обчислити суму додатних членів арифметичної прогресії з додатним першим членом і від’ємною різницею.

Домовимося вводити перший член прогресії в поле Edit1, а її різницю – в поле Edit2.

var a, d, s: Real;

a:= StrToFloat (Edit1.Text);

d:= StrToFloat (Edit2.Text);

s:= 0;

While a > 0 do

s:= s + a;

a:= a + d;

end;

Label1.Caption:= FloatToStr (s);

end;

Виконаємо цей фрагмент програми для деякого набору значень a і d.

Команда	Результат виконання
a:= StrToFloat (Edit1.Text)	a = 7
d:= StrToFloat (Edit2.Text)	d = -3
s:= 0	s = 0
a > 0	(7 > 0) = true
s:= s + a	s = 0 + 7 = 7
a:= a + d	a = 7 +(-3) = 4
a > 0	(4 > 0) = true
s:= s + a	s = 7 + 4 = 11
a:= a + d	a = 4 +(-3) = 1
a > 0	(1 > 0) = true
s:= s + a;	s = 11 + 1 = 12
a:= a + d	a = 1 +(-3) = -2
a > 0	(-2 > 0) = false
Label1.Caption:= FloatToStr (s)	Label1.Caption = 12

Загальний вигляд команди циклу з післяумовою такий:

<команди тіла циклу>

until <логічний вираз>;

( англ. repeat – повторити, until – доки, не раніше як).

Виконується команда циклу з передумовою так:

1. Виконати команди тіла циклу.

2. Обчислити значення логічного виразу.

3. Якщо це значення false, то виконати п.1, а якщо true, то виконати команду, наступну за командою циклу.

Команду циклу з післяумовою доцільно використовувати в тих випадках, коли команди тіла циклу повинні виконатися хоча б один раз.

Проілюструємо, як виглядатиме фрагмент програми для розв’язування попередньої задачі з використанням циклу з післяумовою:

var a, d, s: Real;

a:= StrToFloat (Edit1.Text);

d:= StrToFloat (Edit2.Text);

s:= 0;

s:= s + a;

a:= a + d;

until a <= 0;

Label1.Caption:= FloatToStr (s);

end;

Виконаємо цей фрагмент програми для деякого набору значень a і d.

Команда	Результат виконання
a:= StrToFloat (Edit1.Text)	a = 7
d:= StrToFloat (Edit2.Text)	d = -3
s:= 0	s = 0
s:= s + a	s = 0 + 7 = 7
a:= a + d	a = 7 +(-3) = 4
а <= 0	(4 <= 0) = false
s:= s + a	s = 7 + 4 = 11
a:= a + d	a = 4 +(-3) = 1
а <= 0	(1 <= 0) = false
s:= s + a	s = 11 + 1 = 12
a:= a + d	a = 1 +(-3) = -2
а <= 0	(-2 <= 0) = true
Label1.Caption:= FloatToStr (s)	Label1.Caption = 12

Звертаємо вашу увагу:

1. У команді циклу з післяумовою операторні дужки не використовують незалежно від кількості команд у тілі циклу.

2. Якщо цикл з передумовою замінити на цикл з післяумовою, або навпаки, то логічний вираз одного є запереченням логічного виразу іншого.

Приклади програм з використанням циклів

Розглянемо кілька цікавих і корисних для подальшого вивчення теми задач, в алгоритмах розв’язування яких використовуються цикли.

При розв’язуванні багатьох задач доцільно використовувати ще 2 арифметичні операції: знаходження неповної частки і остачі при діленні цілого числа на натуральне. Нагадаємо, що для будь-якого цілого числа m і натурального числа n існує єдина пара цілих чисел q і r (0 ≤ r < n), таких що m = nq + r. Число q називається неповною часткою, а число r – остачею. Для знаходження неповної частки в Delphi використовується операція div (англ. div ide – поділити), а для знаходження остачі – mod (англ. mod ulo – остача від ділення). Наприклад,

23 div 5 = 4, 23 mod 5 = 3,

28 div 4 = 7, 28 mod 4 = 0,

2 div 3 = 0, 2 mod 3 = 2.

Задача 3. Дано натуральне число n, більше 1. З’ясувати, чи є це число простим.

Нагадаємо, що простим називається натуральне число, яке має рівно 2 дільники. Тому можна перебрати всі натуральні числа від 1 до даного числа і підрахувати кількість дільників даного числа. Якщо ця кількість дорівнює 2, то це число просте, якщо більше – не просте. Відповідний фрагмент програми виглядатиме так:

var i, k, n: Integer;

n:= StrToInt(Edit1.Text);

k:= 0; // Кількість дільників числа n

for i:= 1 to n do

if n mod i = 0 //Перевірка, чи є число i дільником числа n

then k:= k+1; //Збільшення на 1 кількості дільників числа n, якщо число i є його дільником

if k = 2

then Label1.Caption:= 'просте'

else Label1.Caption:= 'не просте';

end;

Функція StrToInt (англ. str ing to int eger– рядок в ціле) використовується для переведення текстового представлення цілого числа в саме ціле число.

Але час виконання програми для розв’язування цієї задачі можна суттєво зменшити, якщо врахувати такі властивості натуральних чисел:

1. Будь-яке натуральне число, більше 1, завжди має 2 дільники (одиницю і саме це число). Тому простим буде таке натуральне число, яке не матиме інших дільників.

2. Серед натуральних чисел тільки одне парне число є простим (2), всі інші прості числа – непарні.

3. Якщо не враховувати саме число, у натурального числа немає дільників, які перевищують арифметичний квадратний корінь з цього числа.

Якщо при складання програми використати вказані властивості, то відповідний фрагмент програми може бути таким:

var i, k, n: Integer; f: Boolean;

n:= StrToInt(Edit1.Text);

f:= true; // Будемо поки що вважати число n простим, адже дільників у нього поки що не знайшлося

if (n mod 2 = 0) and (n <> 2)

then f:= false // Якщо число n парне і не дорівнює 2, то воно не просте

k:= 3; // Якщо число непарне, то будемо шукати його дільники, починаючи з числа 3

while (k <= sqrt(n)) and f do // Шукати дільники числа будемо серед чисел, які не перевищують арифметичний квадратний корінь з числа n, і поки такий дільник не знайшовся

if n mod k = 0 // перевірка, чи є число k дільником числа n

then f:= false

else k:= k + 2; // Якщо k не є дільником n, то наступний можливий дільник – наступне непарне число

end;

then Label1.Caption:= 'просте'

else Label1.Caption:= 'не просте';

end;

У наведеному фрагменті програми використана логічна змінна f. Її значення визначатиме, чи є число n простим чи ні: true – просте, false – не просте. Тип логічної змінної в Delphi позначається Boolean, на честь Джорджа Буля. Для обчислення арифметичного квадратного кореня використана стандартна функція sqrt (англ. sq uare r oo t – квадратний корінь).

Задача 4. Знайти найбільший спільний дільник (НСД) двох даних натуральних чисел a і b (a > b).

У курсі математики 6 класу ви навчилися знаходити НСД чисел, розкладаючи їх на прості множники. Можна скласти програму, в якій реалізується цей метод знаходження НСД.

Але більш простою виявляється програма, яка реалізує інший метод знаходження НСД, що базується на такому математичному твердженні: якщо a > b, то НСД (a, b) = НСД (b, r), де r – остача від ділення a на b. Ідея цього методу полягає в тому, що послідовно замінюються числа, для яких потрібно знайти НСД: більше з них замінюється на менше, а менше – на остачу від ділення більшого числа на менше. Закінчується цей процес замінювання тоді, коли остача від ділення стає рівною нулю. Тоді НСД дорівнює останній відмінній від 0 остачі від ділення.

Наприклад,

НСД(80, 12) = НСД(12, 8) = НСД(8, 4) = НСД(4,0) = 4,

НСД(125, 54) = НСД(54, 17) = НСД(17, 3) = НСД(3,2) = НСД(2,1) = НСД(1, 0) = 1.

Цей метод знаходження НСД називається алгоритмом Евкліда. Перевірте цей метод знаходження НСД для різних пар натуральних чисел.

Нижче наведений фрагмент програми, в якому знаходиться НСД двох чисел за алгоритмом Евкліда.

var a, b, r: Integer;

a:= StrToInt(Edit1.Text);

b:= StrToInt(Edit2.Text);

r:= a mod b;

while r <> 0 do

a:= b;

b:= r;

r:= a mod b;

end;

Label1.Caption:= IntToStr (b);

end;

Звертаємо вашу увагу, що наведений фрагмент програми працює правильно і в тих випадках, коли
a ≤ b. Спробуйте самостійно з’ясувати, чому.

Цікаві факти з історії

Евклід ( біля300 р. до н. е. – біля 265 р. до н.е.) (рис. 2.58) – відомий давньогрецький математик. Основною заслугою Евкліда вважається його величезна робота по збиранню і систематизації усіх відомих на той час математичних фактів геометрії та арифметики у 13 книгах, які він назвав «Початки».

Історики математики знайшли підтвердження того, що алгоритм Евкліда для знаходження НСД був відомий ще й до Евкліда. А причиною того, що його назвали на честь Евкліда, напевне є те, що Евклід уперше його детально описав у своїх «Початках».

Рис. 2.58. Евклід

Перевірте себе

1. º Що таке цикл в алгоритмі?

2. ^· Наведіть блок-схему циклу з передумовою. Поясніть виконання цього циклу. Наведіть приклади циклів з передумовою.

3. ^· Наведіть блок-схему циклу з післяумовою. Поясніть виконання цього циклу. Наведіть приклади циклів з післяумовою.

4. ^· Чи можуть команди тіла циклу не виконуватись жодного разу? Поясніть свою відповідь. Наведіть приклади.

5. * Чи може виконання циклу ніколи не закінчитися? Поясніть свою відповідь. Наведіть приклади.

6. ^· Поясніть відмінності у виконанні основних алгоритмічних структур: слідування, розгалуження, цикл.

7. º Наведіть загальний вигляд команди циклу з лічильником в Delphi.

8. ^· Поясніть виконання команди циклу з лічильником в Delphi.

9. º Наведіть загальний вигляд команди циклу з передумовою і команди циклу з післяумовою в Delphi.

10. ^· Поясніть виконання команди циклу з передумовою і команди циклу з післяумовою в Delphi.

11. * Поясніть відмінності у використанні команд циклу з параметром та циклу з передумовою в Delphi.

12. * Поясніть відмінності у використанні команд циклу з передумовою та циклу з післяумовою в Delphi.

Виконайте завдання

1. Виконайте алгоритми:

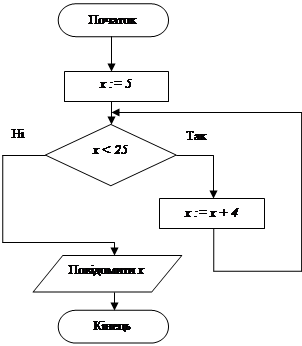
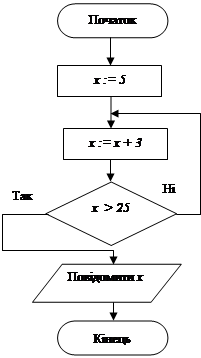а)º б) ^·

2. (ДЗ) Виконайте алгоритми:

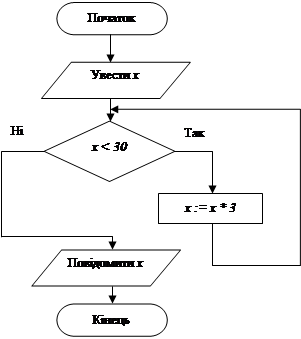а) º б) ^·

3. ^· Виконайте в таблиці фрагмент програми та з’ясуйте, якими будуть значення змінних після його завершення:

а) р:= 1; a:= 2; б) k:= 1; a:= 12; в) s:= 0; a:= 1; k:= 1;

for i:= 1 to 5 do while a < 100 do repeat

begin begin s:= s + a;

a:= 3*a + 1; а:= 2*а – 4; k:= k + 1;

р:= р * a; k:= k + 1; a:= k * k;

end; end; until a > 50;

4. (ДЗ) ^· Виконайте фрагмент програми та з’ясуйте, якими будуть значення змінних після його завершення:

а) p:= 1; a:= 8; б) k:= 1; a:= 100; в) s:= 0; a:= 5428;

for i:= 1 to 4 do while a > 10 do repeat

begin begin c:= a mod 10;

a:= 2*a – 5; а:= а div 2; s:= s + c;

р:= р * a; k:= k + 1; a:= a div 10;

end; end; until a < 1;

5. ^· Виконайте в таблиці фрагмент програми для задачі 3, наведеної в тексті пункту.

6. (ДЗ) ^· Виконайте в таблиці фрагмент програми для задачі 4, наведеної в тексті пункту.

7. º Складіть блок-схему алгоритму знаходження суми перших 5 членів послідовності, перший член якої х = 7, а кожен наступний обчислюється на основі попереднього значення за формулою х:= 2*х + 3. Виконайте алгоритм.

8. (ДЗ) º Складіть блок-схему алгоритму знаходження добутку перших 8 членів арифметичної прогресії з першим членом, рівним 9 та різницею 4. Виконайте алгоритм.

9. ^· Складіть блок-схему алгоритму знаходження кількості додатних членів арифметичної прогресії з відомим першим членом та різницею -5. Виконайте алгоритм для трьох різних значень першого члену прогресії. Підберіть ці значення так, щоб команди тіла циклу виконались кілька разів; один раз; жодного разу.

10. (ДЗ) ^· Складіть блок-схему алгоритму знаходження суми двоцифрових членів арифметичної прогресії з першим членом 25 та відомою різницею. Виконайте алгоритм для трьох різних значень різниці прогресії. Підберіть ці значення так, щоб команди тіла циклу виконались кілька разів; один раз; жодного разу.

11. * Складіть блок-схему алгоритму розв’язання задачі: визначити, на скільки квадратів можна розрізати прямокутну смужку паперу з заданими довжиною та шириною, якщо на кожному кроці від смужки відрізати квадрат, сторона якого дорівнює менший із сторін смужки, що залишилась після попереднього відрізу. Виконайте алгоритм для двох різних значень початкових даних. Підберіть ці значення так, щоб команди тіла циклу виконались кілька разів; один раз.

12. ^· Створіть проект, в якому можна обчислити добуток перших N членів послідовності чисел, перше з яких дорівнює x, а кожне наступне удвічі менше попереднього. Створіть у власній папці папку Проект 2.9.12 і збережіть у ній проект.

13. (ДЗ) ^· Створіть проект, в якому можна обчислити суму перших N членів послідовності чисел, перше з яких дорівнює x, а кожне наступне дорівнює квадрату попереднього. Створіть у папці Мої документи папку Проект 2.9.13 і збережіть у ній проект.

14. ^· Створіть проект, в якому можна обчислити кількість двоцифрових чисел у арифметичній прогресії. Перший член прогресії більший від 10, різниця більше нуля. Створіть у власній папці папку Проект 2.9.14 і збережіть у ній проект.

15. (ДЗ) ^· Створіть проект, в якому можна обчислити середнє арифметичне членів геометричної прогресії, що більші за одиницю. Перший член прогресії більший від 100, знаменник менше від одиниці, але більший нуля. Створіть у папці Мої документи папку Проект 2.9.15 і збережіть у ній проект.

16. ^· Створіть проект, в якому можна знайти кількість дільників заданого натурального числа. Створіть у власній папці папку Проект 2.9.16 і збережіть у ній проект.

17. * Створіть проект, в якому можна обчислити кількість простих чисел серед перших 100 натуральних чисел. Створіть у власній папці папку Проект 2.9.17 і збережіть у ній проект.

18. ^· Створіть проект для розв’язання задачі: Людина поклала у банк певну суму грошей. Щорічно банк додає до суми наперед визначений відсоток від суми, що зберігається на рахунку після попереднього року. Яка сума буде на рахунку через N років? Створіть у власній папці папку Проект 2.9.18 і збережіть у ній проект.

19. (ДЗ) ^· Створіть проект для розв’язання задачі: Людина поклала у банк певну суму грошей. Щорічно банк додає до суми наперед визначений відсоток від суми, що зберігається на рахунку після попереднього року. Через скільки років сума на рахунку стане не меншою від S грн? Створіть у папці Мої документи папку Проект 2.9.19 і збережіть у ній проект.

20. * Створіть проект для обчислення суми цифр заданого натурального числа, кількість цифр якого не більше 9. Створіть у власній папці папку Проект 2.9.20 і збережіть у ній проект.

Практична робота № 9

«Програмування циклічних обчислень»

Увага! Під час роботи з комп’ютером дотримуйтеся правил безпеки та санітарно-гігієнічних норм.

1. Відкрийте середовище візуального проектування Turbo Delphi 2006.

2. Створіть проект для розв’язування задачі: Перед початком повені рівень води у річці становив Н метрів. Під час повені кожну годину рівень води зростав на Р відсотків від рівня попередньої години. Яким буде рівень води через N годин після початку повені? Через скільки годин після початку повені рівень води буде не менше, ніж К метрів?

1. Розмістіть на формі поля для введення початкових даних, написи із текстами, що будуть пояснювати їхні призначення та три кнопки.

2. Установіть на першій кнопці напис Питання 1, на другій – Питання 2, на третій – Спочатку, у полів – порожній текст.

3. Складіть обробник події OnClick першої кнопки, виконання якого приведе до виведення у вікно повідомлення відповіді на перше запитання задачі.

4. Виконайте складену процедуру і переконайтеся, що результати її роботи правильні.

5. Складіть обробник події OnClick другої кнопки, виконання якого приведе до знаходження відповіді на друге запитання задачі і виведення його в окремий напис.

6. Виконайте складену процедуру і переконайтеся, що результати її роботи правильні.

7. Складіть обробник події OnClick третьої кнопки, виконання якого призведе до очищення тексту у полях та напису з відповіддю на друге запитання задачі.

3. Створіть у власній папці папку Практична 9 і збережіть у ній проект.

2.10. Процедури і функції користувача та стандартні процедури і функції в Delphi

Пригадайте!

1. Що таке процедура?

2. Що таке обробник події? Як створити обробник події?

3. Який загальний вигляд процедур-обробників подій, які ви створювали в Delphi?

4. Які змінні називаються локальними, а які глобальними? Поясніть різницю між ними.

5. Як у Delphi змінити числовий тип змінної на текстовий і навпаки?

Процедури користувача в Delphi

У попередніх пунктах ви створювали і використовували процедури, які були пов’язані з певними подіями і були методами певних об’єктів. Заготовки цих процедур середовище розробки створювало автоматично, а ви доповнювали ці заготовки командами і рядком var опису змінних.

При створенні програм можна включати до проекту процедури, не пов’язані з подіями. Такі процедури називаються процедурами користувача. Їх найчастіше використовують у випадках, коли потрібно кілька разів при різних значеннях змінних виконувати одні й ті самі операції: обчислювати площу і периметр трикутників або інших геометричних фігур, вибирати більше з двох чисел, визначати, просте число чи ні, та інші. Або коли задачу можна поділити на окремі підзадачі, кожна з яких розв’язується за окремим алгоритмом, тобто при використанні методу покрокової деталізації.

Дата добавления: 2014-11-29