Ітераційний алгоритм розв'язання транспортної задачі

Метод Фогеля

Метод найменшого елементу

Даний метод знаходить краще початкове рішення, ніж метод північно-західного кута, оскільки вибирає змінні, яким відповідають найменші вартості. Спочатку по всій транспортній таблиці ведеться пошук осередку з найменшою вартістю. Потім змінній в цій клітинці присвоюється найбільше значення, яке визнається обмеженнями на попит і пропозицію. Якщо таких змінних кілька, вибір довільний. Далі викреслюється відповідний стовпець або рядок, і відповідним чином коректуються значення попиту і пропозицій. Потім проглядаються невикреслені клітинки, і вибирається нова клітинка, із мінімальною вартістю. Описаний процес продовжується до тих пір, поки не залишиться лише один невикреслений рядок або стовпець.

Цей метод більш складний, однак він дає найкраще початкове рішення.

Алгоритм виконання методу.

1. У кожному рядку і кожному стовпці транспортної таблиці обчислюється різниця між двома найменшими елементами (C_ij).

2. Серед всіх виявлених різниць Cij обирається максимальна і виділяється відповідний стовпець (рядок).

3. В обраному стовпці (рядку) знаходиться мінімальне значення Cij і призначається необхідне перевезення, орієнтуючись на наявність запасів (a_i) даного постачальника (A_ij) і потреб (b_j) даного споживача (B_ij).

4. Викресливши відповідний рядок (стовпчик). Тобто, видаливши з подальших розрахунків постачальника (споживача), запаси якого (потреби) вичерпані, повторити заново кроки (1-4) до повного складання плану перевезень.

Процес розподілу продовжують до тих пір, поки всі вантажі від постачальників не будуть вивезені, а споживачі не будуть задоволені.

Після визначення початкового рішення (за допомогою одного з трьох методів) застосовується алгоритм, що дозволяє знайти оптимальне рішення транспортної задачі.

Знайдене вихідне опорне рішення перевіряється на оптимальність методом потенціалів за наступним критерієм: якщо опорне рішення транспортної задачі є оптимальним, то йому відповідає система mn дійсних чисел u_i і _vj, що задовольняють умовам u_iv_j = c_ij для зайнятих клітин і u_i v_j-c_ij ≤ 0 для вільних клітин.

Числа u_i і v_j називають потенціалами. В транспортну таблицю додають рядок v_j і стовпець u_i.

Потенціали u_i і v_j знаходять з рівності u_iv_j = c_ij, справедливого для зайнятих клітин. Одному з потенціалів дається довільне значення, зазвичай u₁ = 0, тоді інші потенціали визначаються однозначно. Так, якщо відомий потенціал u_i, то v_j = c_ij-u_i; якщо відомий потенціал v_j, то u_i = c_ij-v_j.

Позначимо Δ_ij = u_i+v_j-c_ij. Цю оцінку називають оцінкою вільних клітин. Якщо Δ_ij ≤ 0, то опорне рішення є оптимальним. Якщо хоча б одна з оцінок Δ_ij> 0, то опорне рішення не є оптимальним і його можна поліпшити, перейшовши від одного опорного рішення до іншого.

Обчислені значення спільно з нульовими значеннями для базисних змінних (оскільки u_i+ v_j-c_ij = 0 для будь-якої базисної змінної x_ij) фактично є коефіцієнтами z-рядка симплекс-таблиці.

Оскільки в транспортній задачі ведеться пошук мінімуму вартості перевезень, змінною, що вводиться в базис, буде змінна, яка має найбільший позитивний коефіцієнт у z-рядку.

Визначивши змінну, що вводиться в базис, далі слід знайти виключаємо з базису змінну. Нагадаємо, якщо яка-небудь змінна вводиться в базис, одна з поточних базисних змінних повинна стати небазісной (і рівною нулю), щоб кількість базисних змінних залишалася постійною.

Змінна, яка виключається з базису, визначається наступним чином. Позначимо через q кількість вантажу, що перевозиться за маршрутом, відповідним до змінної, що вводиться. Максимально можливе значення q визначаємо з наступних умов.

1. Повинні виконуватися обмеження на попит і пропозицію.

2. Ні за яким маршрутом не повинні виконуватися перевезення з від’ємним обсягом вантажів.

Ці умови дозволяють знайти значення q і визначити змінну, яка виключається.

Спочатку побудуємо замкнутий цикл, який починається і закінчується в клітинці, відповідній змінній, що вводиться. Цикл складається з послідовності горизонтальних і вертикальних відрізків (але не діагональних), що з'єднують клітинки, відповідні до поточних базисних змінних, і клітинку, відповідну до змінної, що вводиться. Для будь-якої змінної, що вводиться, можна побудувати тільки один замкнутий цикл.

Тепер знайдемо значення q. Для того щоб задовольнити обмеженням по попиту і пропозиції, треба по черзі віднімати і додавати q до значень базисних змінних, розташованих в кутових клітинках циклу (не має значення напрямок обходу циклу: за годинниковою стрілкою або проти).

Нові значення базисних змінних залишаться невід'ємними, якщо значення q не буде перевищувати мінімального значення базисної змінної, від якої віднімається q. Таким чином, q буде приймати мінімальне значення базисної змінної циклу від якої здійснюється віднімання. При цьому дана базисна змінна після віднімання набуде значення 0. Це і буде змінна, що вводиться. Якщо одночасно кілька базисних змінних набудуть значення 0, то тільки одна з них (будь-яка) вийде з базису.

Визначивши значення для змінної, що вводиться, і вибравши змінну, що виводиться, далі слід відкоригувати значення базисних змінних, відповідних кутовим клітинкам замкнутого циклу.

Маючи нове базисне рішення, слід повторити обчислення потенціалів і перевірити нове рішення на оптимальність. Якщо нове рішення є неоптимальним, перерахунок повторюється.

3.2 Завдання на виконання лабораторної роботи

3.2.1 Постановка задачі

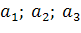Є три пункти постачання однорідного вантажу – і п'ять пунктів споживання цього вантажу . У пунктах знаходиться вантаж відповідно. Вантаж необхідно доставити в пункти у кількості 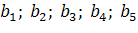відповідно. Відстані між пунктами в кілометрах задані наступного матрицею:

.

(3.3)

Потрібно знайти оптимальний план закріплення споживачів за постачальниками однорідного вантажу за умови мінімізації загального пробігу автомобілів, використовуючи варіанти, представлені нижче.

3.2.2 Порядок виконання роботи

1. Для транспортної задачі згідно варіанту знайти початковий план методом Північно-Західного кута (або методом найменшого елементу).

2. Знайти оптимальне рішення транспортної задачі методом потенціалів.

3. Знайти початковий план методом Фогеля і порівняти його з оптимальним рішенням.

4. Розв’язати задачу з використанням мови ampl.

Таблиця 3.2 Варіанти завдань
№ варіанту	Модель

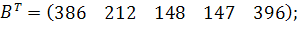
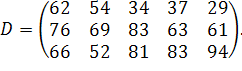
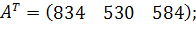
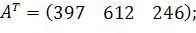
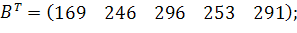
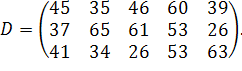
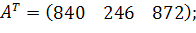
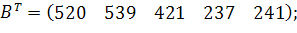
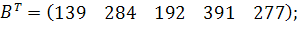
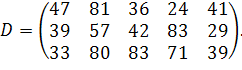
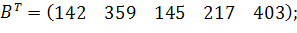
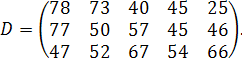
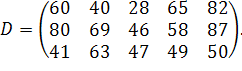
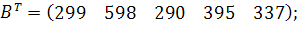
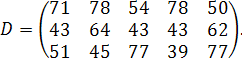
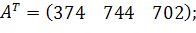
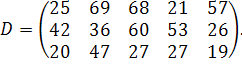
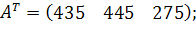
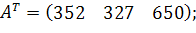
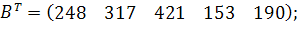
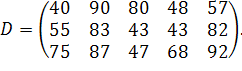
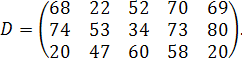
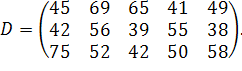
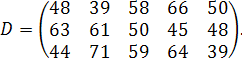
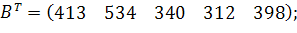
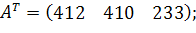
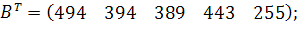
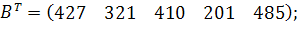
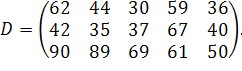
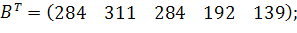
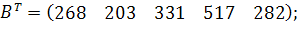
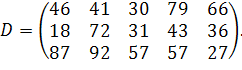
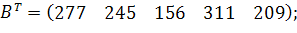
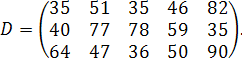
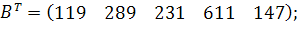
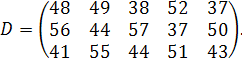
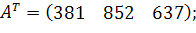
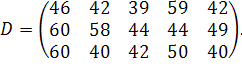
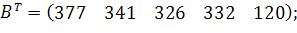
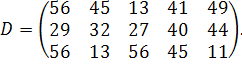
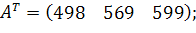
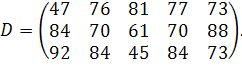
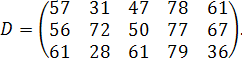
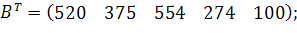
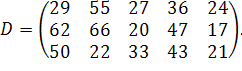
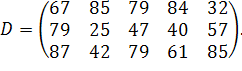
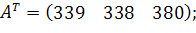
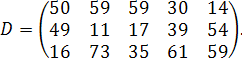
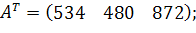
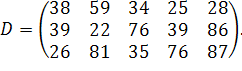
Приклад розв'язання задачі із застосуванням мови ampl для моделі:

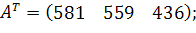
1. Необхідно створити файл з описанням моделі. Нижче надано листинг файла transportation.mod.

# transportation.mod

set SHIPPERS;

set CONSUMERS;

param availability { SHIPPERS } >= 0;

param demand { CONSUMERS } >= 0;

param distance { SHIPPERS, CONSUMERS } >= 0;

var x { SHIPPERS, CONSUMERS } >= 0, integer;

minimize cost:

sum {i in SHIPPERS, j in CONSUMERS} distance[i,j] * x[i,j];

subject to avail {i in SHIPPERS}:

sum {j in CONSUMERS} x[i,j] = availability[i];

subject to request {j in CONSUMERS}:

sum {i in SHIPPERS} x[i,j] = demand[j];

data;

set SHIPPERS:= A1 A2 A3;

set CONSUMERS:= B1 B2 B3 B4 B5;

param availability:=

A1 581

A2 559

A3 436;

param demand:=

B1 274

B2 238

B3 345

B4 532

B5 187;

param distance:

B1 B2 B3 B4 B5:=

A1 93 34 95 29 84

A2 96 86 53 47 27

A3 27 38 61 28 91;

2. У командному рядку ampl необхідно виконати наступні команди:

model transportation.mod;

option solver cplex;

solve;

display cost;

display x;

Перша команда завантажує модель з файлу transportation.mod.

Друга команда встановлює розв’язуючу програму (solver). У даному випадку використовується студентська версія CPLEX.

Третя команда запускає безпосередньо процедуру розв’язку.

Останні дві команди виводять результати на екран.

Результат виконання команд представлений в наступному лістингу.

sw: ampl

ampl: model transportation.mod;

ampl: option solver cplex;

ampl: solve;

CPLEX 11.2.0: optimal integer solution; objective 54576

5 MIP simplex iterations

0 branch-and-bound nodes

ampl: display cost;

cost = 54576

ampl: display x;

x:=

A1 B1 0

A1 B2 238

A1 B3 0

A1 B4 343

A1 B5 0

A2 B1 0

A2 B2 0

A2 B3 345

A2 B4 27

A2 B5 187

A3 B1 274

A3 B2 0

A3 B3 0

A3 B4 162

A3 B5 0;

3.3 Контрольні питання

1. Які задачі лінійного програмування можна віднести до транспортних задач? Яке їх призначення?

2. Математична постановка транспортної задачі?

3. Що вважають оптимальним рішенням транспортної задачі?

4. Послідовність етапів алгоритму розв'язання транспортної задачі?

5. У чому полягає метод північно-західного кута?

6. У чому полягає метод найменшого елементу?

7. У чому полягає метод Фотеля?

8. Як знайти оптимальне рішення транспортної задачіметодом потенціалів?

ЛАБОРАТОРНА РОБОТА № 4
РІШЕННЯ ЗАДАЧ цілочисельного ПРОГРАМУВАННЯ

4.1 Теоретичні зведення

4.1.1 Метод гілок і меж для вирішення задач ЦП

Методи рішення задач цілочисельного лінійного програмування засновані на використанні обчислювальних можливостей методів лінійного програмування. Зазвичай алгоритми цілочисельного програмування включають три кроки.

Крок 1. "Ослаблення" простору допустимих рішень задачі цілочисельного лінійного програмування шляхом заміни будь-якої двійкової змінної 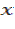безперервним обмеженням і відкидання вимоги цілочисельності для всіх інших змінних. У результаті виходить звичайне завдання лінійного програмування.

Крок 2. Розв’язання задачі лінійного програмування та визначення її оптимального рішення.

Крок 3. Маючи отримане (безперервне) оптимальне рішення, додаємо спеціальні обмеження, які ітераційним шляхом змінюють простір допустимих рішень задачі лінійного програмування таким чином, щоб в кінцевому рахунку вийшло оптимальне рішення, яке задовольняє вимогам цілочисельності.

Розроблено два загальних методи генерування спеціальних обмежень, про які йде мова при реалізації кроку 3.

1. Метод гілок і меж.

2. Метод відтинаючих площин.

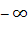Сформулюємо алгоритм методу гілок і меж у загальному випадку. Припустимо, що розглядається задача максимізації. Задамо нижню межу оптимального значення цільової функції задачі ЦЛП рівною . Покладемо .

Крок 1. (Зондування і визначення межі). Вибираємо i -у підзадачу лінійного програмування ЛП i для дослідження. Розв’язуєємо ЛП i і зондуємо її, при цьому можлива одна з трьох ситуацій:

1. Оптимальне значення цільової функції задачі ЛП i не може поліпшити поточної нижньої межі.

2. ЛП i призводить до кращого допустимого цілочисельного рішення, ніж поточна нижня межа.

3. ЛП i не має допустимих рішень.

Можливі два варіанти:

1. Якщо задачу ЛП і прозондувати, нижня межа змінюється тільки за умови, що знайдено найкраще рішення задачі ЦЛП. Якщо всі підзадачі прозондувати, необхідно закінчити обчислення: оптимальним рішенням задачі ЦЛП стане те, що відповідає поточній нижній межі, якщо така існує. Інакше покласти 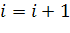і повторити крок 1.

2. Якщо задача ЛП i НЕ прозондована, переходимо до кроку 2 для виконання гілкування.

Крок 2. (Гілкування). Вибираємо одну з цілочисельних змінних 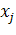, оптимальне значення 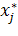якої в оптимальному розв'язанні задачі ЛП i не є цілим числом. Виключаємо з простору допустимих рішень область (де [v] - найбільше ціле, що не перевершує v) шляхом формування двох підзадач ЛП, які відповідають обмеженням і .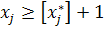

Покладемо 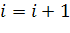і переходимо до кроку 1.

Описаний алгоритм застосовується для розв’язання задач максимізації. Для розв’язку задач мінімізації в алгоритмі необхідно замінити нижню межу верхньою (початкове значення якої дорівнює ).

Алгоритм методу гілок і меж безпосередньо поширюється на задачі частково-цілочисельного ЛП (в яких лише деякі зі змінних повинні приймати цілочисельні значення). Якщо деяка змінна є безперервною, то вона ніколи не обирається в якості змінної гілкування. Допустима підзадача визначає нову межу для значення цільової функції, якщо значення дискретних змінних є цілочисельними і значення цільової функції покращено у порівнянні з поточною межею.

4.2 Завдання на виконання лабораторної роботи

Розв’язати задачу цілочисельного програмування методом гілок і меж.

Таблиця 4.1 Варіанти завдань
№ варіанту	Модель

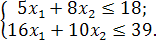
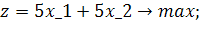
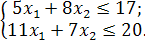
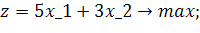
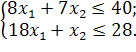
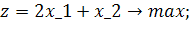
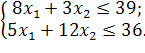
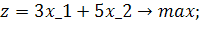
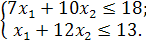
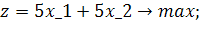
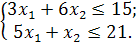
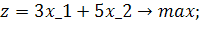
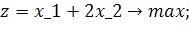
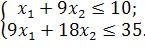
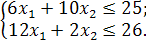
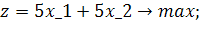
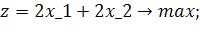
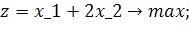
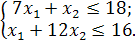
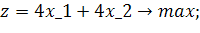
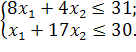
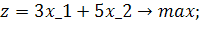
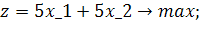
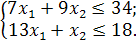
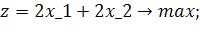
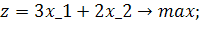
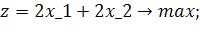
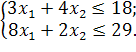
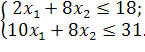
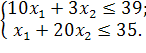
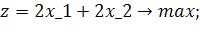
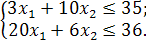
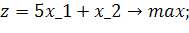
4.3 Контрольні питання

1. Які задачі можна віднести до цілочисельного лінійного програмування?

2. Які існують методи розв’язання задач цілочисельного лінійного програмування?

3. Назвіть кроки, що включають алгоритми цілочисельного програмування?

4. Сформулюйте алгоритм методу гілок і меж у загальному випадку?

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Хемди А. Таха Введение в исследование операций. - М.: <<Вильямс>>, 2007.

2. Дегтярёв Ю. И. Исследование операций: учеб. для вузов по спец. АСУ.-М.: Высш. шк., 1986

3. Вентцель Е. С. Исследование операций: задачи, принципы, методология. - М.: Наука, 1980

4. Конюховский П. Математические методы исследования операций в экономике. Учебное пособие. СПб: Питер. 2000г.

5. Исследование операций в экономике. Под ред. Н.Ш. Кремера М.: Юнити 2003г.

6. Хеллман О. Введение в теорию оптимального поиска. Оптимизация и исследование операций. Перевод с англ. - М.: Наука 1985г.

7. Чернов В.П. Введение в линейное программирование. – СПб: Наука 2002г.

8. Лунгу К.Н. Линейное программирование. Руководство к решению задач. - М. Физматлит 2005г.

9. Васильев Ф., Иваницкий А. Линейное программирование. - М.: Факториал 2008г.

Дата добавления: 2014-11-29