
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение гистограммы распределения погрешностей
|
|
|
|
Определение среднеквадратической погрешности результата измерения
Вычислить значение среднеквадратической погрешности результата измерения, т.е. погрешности σA, с которой определено среднеарифметическое значение Rср: 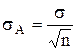 . Результаты вычисления включить в табл. 1.1. При этом обратить внимание на то, что при увеличении числа наблюдений в n раз среднеквадратическая погрешность результата измерения уменьшается в
. Результаты вычисления включить в табл. 1.1. При этом обратить внимание на то, что при увеличении числа наблюдений в n раз среднеквадратическая погрешность результата измерения уменьшается в  раз по сравнению с погрешностью отдельного наблюдения.
раз по сравнению с погрешностью отдельного наблюдения.
Указанное построение проводится для качественной проверки соответствия закона распределения погрешностей, полученных при многократных наблюдениях, нормальному закону распределения. Построение гистограммы провести в следующем порядке.
 1 Выбрать величину интервала статистического ряда погрешностей а (рис.1.3), для чего по табл.1.1 найти наибольшие по величине остаточные погрешности
1 Выбрать величину интервала статистического ряда погрешностей а (рис.1.3), для чего по табл.1.1 найти наибольшие по величине остаточные погрешности 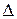 Ri разных знаков, по их разности определить диапазон наблюдаемых погрешностей b, разделить его на число интервалов r. Тогда интервал a = b/r. Принять r = 6. Если b не делится на r точно, то частное округлить до одной – двух значащих цифр.
Ri разных знаков, по их разности определить диапазон наблюдаемых погрешностей b, разделить его на число интервалов r. Тогда интервал a = b/r. Принять r = 6. Если b не делится на r точно, то частное округлить до одной – двух значащих цифр.
2 Заполнить таблицу статистического ряда (табл.1.2). Для этого по табл.1.1 подсчитать число Sj остаточных погрешностей, лежащих в интервале 0 – a, а – 2 а, 2 а – 3 а отдельно с плюсом и минусом. Числа Sj записать в табл. 1.2. В ту же таблицу внести частоты появления погрешностей, определяемые для каждого интервала как отношение числа погрешностей Sj к общему числу погрешностей n. Погрешности, точно совпадающие по значению с границей интервала, могут быть отнесены либо к j–1 интервалу, либо к j интервалу. Например, если таких погрешностей две, то их целесообразно разделить между смежными интервалами. Для определения высот прямоугольников гистограммы (см. рис.1.3) нужно частоты появления погрешностей разделить на величину интервалов. Вычисленные значения Sj/n a внести в табл.1.2.
Таблица 1.2
| Интервалы | 0 – a | a – 2 a | 2 a – 3 a | |||
| Знак погрешностей | + | – | + | – | + | – |
| Число остаточных погрешностей Sj | ||||||
| Частоты появления погрешностей Sj / n | ||||||
| Высоты прямоугольников гистограммы Sj / n a | ||||||
Середины интервалов 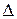 Ri Ri
| ||||||
P(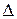 Ri) Ri)
|
3 Построить гистограмму, для чего по оси абсцисс отложить численные значения интервалов ± a, ±2 a, ±3 a. На каждом интервале, как на основании построить прямоугольник, площадь которого равна частоте появления погрешностей, лежащих в данном интервале. Значения высот прямоугольников взять из табл.1.2. Площадь гистограммы равна единице (из построения).
4 Построить на том же графике теоретическую кривую нормального распределения в соответствии с уравнением (1.1). Значения P(DRi) определить для точки DRi = 0 и середин интервалов DRi = ± a /2; ±3 a /2, ±5 a /2. Полученные значения занести на построенную гистограмму. Соединить нанесенные точки плавной кривой. Сравнить гистограмму с теоретической кривой нормального распределения.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1711; Нарушение авторских прав?; Мы поможем в написании вашей работы!