Свободные затухающие и вынужденные механические колебания

Во всякой реальной системе, совершающей механические колебания, всегда действуют те или иные силы сопротивления (трение в точке подвеса, сопротивление окружающей среды и т.п.), на преодоление которых система затрачивает энергию, вследствие чего реальные свободные механические колебания всегда являются затухающими.

Затухающие колебания - это колебания, амплитуда которых убывает со временем.

Найдем закон изменения амплитуды.

Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы 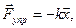сила трения пропорциональна скорости:

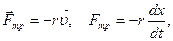
где r - коэффициент сопротивления среды; знак минус означает, что всегда направлена противоположно скорости.

Согласно II закону Ньютона уравнение движения маятника имеет вид:

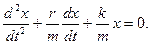
Обозначим: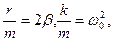

дифференциальное уравнение свободных затухающих колебаний.

Решением этого уравнения является выражение:

,

где 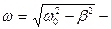циклическая частота свободных затухающих колебаний,

w₀ - циклическая частота свободных незатухающих колебаний,

b - коэффициент затухания,

A₀ - амплитуда в начальный момент времени (t=0).

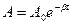- закон убывания амплитуды.

С течением времени амплитуда убывает по экспоненциальному закону (рис. 3).

Время релаксации - это время, за которое амплитуда уменьшается в 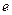раз.

.

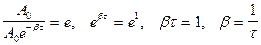Таким образом, есть величина, обратная времени релаксации.

Важнейшей характеристикой затухающих колебаний является логарифмический декремент затухания .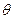

Логарифмическим декрементом затухания называется натуральный логарифм отношения двух амплитуд, отличающихся друг от друга по времени на период:

.

Выясним его физический смысл.

За время релаксации система успеет совершить N колебаний:

,

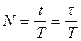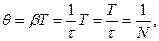
т.е. 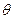- это величина, обратная числу колебаний, в течение которых амплитуда уменьшается в е раз.

Для характеристики колебательной системы используют понятие добротности:

.

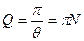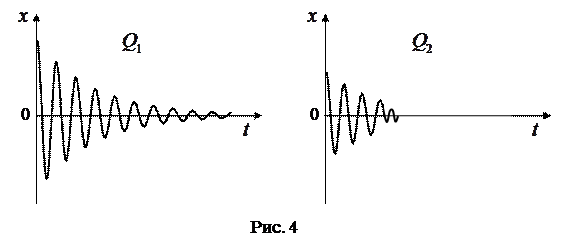
Добротность - физическая величина, пропорциональная числу колебаний, в течение которых амплитуда уменьшается в е раз (рис. 4, ).

Вынужденными называются колебания, которые совершаются в системе под действием периодически изменяющейся внешней силы.

Пусть внешняя сила изменяется по гармоническому закону:

.

Кроме внешней силы на колеблющуюся систему действуют возвращающая сила и сила сопротивления, пропорциональная скорости колебаний:

Вынужденные колебания совершаются с частотой, равной частоте вынуждающей силы. Экспериментально установлено, что смещение 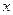отстает в своем изменении от вынуждающей силы. Можно доказать, что

где - амплитуда вынужденных колебаний,

- разность фаз колебани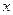й и ,

; .

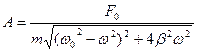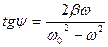Графически вынужденные колебания представлены на рис.5.

Если вынуждающая сила изменяется по гармоническому закону, то и сами колебания будут гармоническими. Их частота равна частоте вынуждающей силы, а амплитуда пропорциональна амплитуде вынуждающей силы.

Зависимость амплитуды от частоты вынуждающей силы приводит к тому, что при некоторой, определенной для данной системы частоте, амплитуда достигает максимума.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте системы (к резонансной частоте) называется резонансом (рис.6).

Дата добавления: 2014-12-07