Контрольная работа. Задача линейного программирования

Транспортная задача

Задача линейного программирования

Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В и С. Потребность a_ij i -го вида сырья для производства каждой единицы j -го вида продукции, запас b_i соответствующего вида сырья и прибыль c_j от реализации единицы j -го вида продукции заданы таблицей:

Виды сырья	Виды продукции	Запасы сырья
I	II
A	a 11 = n	a 12 = 2	b 1 = mn +5 n
B	a 21 = 1	a 22 = 1	b 2 = m + n +3
C	a 31 = 2	a 32 = m + 1	b 3 = mn + 4 m + n + 4
прибыль	c 1 = m +2	c 2 = n + 2
план (ед.)	x 1	x 2

1. Для производства двух видов продукции I и II с планом x ₁ и x ₂ единиц составить математическую модель, т.е. целевую функцию прибыли F и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее n единиц обоих видов продукции.

2. Найти оптимальный план X * = (x ₁, x ₂) производства продукции, обеспечивающий максимальную прибыль F_max. Определить остатки каждого вида сырья. Задачу решить симплекс-методом.

3. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим методом. Определить максимальную прибыль F_max.

4. Составить математическую модель двойственной задачи (систему ограничений по единичной прибыли и целевую функцию общих издержек на сырье Z); найти оптимальный набор цен на сырьё Y *=(y ₁, y ₂, y ₃), обеспечивающий минимум общих затрат на сырье Z_min.

5. Провести анализ первоначальных и дополнительных переменных исходной и двойственной задач, сделать выводы.

6. Решить задачу оптимизации в MS Excel в режиме «поиск решения». Провести исследование полученного решения, используя отчеты по результатам, по устойчивости, по пределам; сделать выводы. Ответы, полученные в результате решений «вручную» и с помощью Excel, должны совпадать.

Решение типовой задачи с использованием Excel представлено в Приложении B.

На трех складах А ₁, А ₂ и А ₃ хранится а ₁=100, а ₂=200, а ₃=60+10 n единиц одного и того же груза, соответственно. Этот груз требуется доставить трем потребителям В ₁, В ₂ и В ₃, заказы которых b ₁=190, b ₂=120, b ₃=10 m единиц груза, соответственно. Стоимости перевозок c_ij единицы груза с i -го склада j -му потребителю указаны в соответствующих клетках транспортной таблицы:

Потребности Запасы	В 1	В 2	В 3
b 1=190	b 2=120	b 3=10 m
А 1	а 1 = 100			m
А 2	а 2 = 200	n
А 3	а 3 = 60 + 10 n		m + 1

1. Сравнивая суммарный запас и суммарную потребность

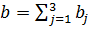в грузе, установить, является ли модель транспортной задачи открытой или закрытой. Если модель открытая, то ее необходимо закрыть, добавив фиктивный склад А ₄ с запасом а ₄= b - а в случае а < b или фиктивного потребителя В ₄ с потребностью b ₄= a - b в случае а > b и положив соответствующие им тарифы перевозок нулевыми.

2. Составить первоначальный план перевозок методом северо-западного угла и методом наименьшей стоимости.

3. Методом потенциалов проверить первоначальный план перевозок на оптимальность в смысле суммарной стоимости перевозок, и если это не так, то составить оптимальный план

,

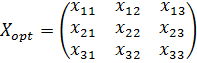обеспечивающий минимальную стоимость перевозок 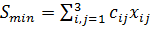. Найти эту стоимость.

4. Решить задачу в MS Excel в режиме «поиск решения». Ответы (значения стоимости перевозок), полученные в результате решений «вручную» и с помощью Excel, должны совпадать. Оптимальные планы перевозок могут не совпадать.

Решение типовой задачи с использованием Excel см. в Приложении С.

Приложение А

Пермский институт (филиал)

ФГБОУ ВПО «Российский государственный торгово-экономический университет»

Кафедра высшей и прикладной математики

по дисциплине:

«Методы оптимальных решений»

на тему:

« Численные методы поиска стационарных точек в оптимизационных задачах: градиентные методы »

Вариант 5 (m =4, n =5)

Выполнила:

студентка группы Эки-21

Суханова Любовь Сергеевна

№ зач. кн. ….04

Проверил:

О.Ю. Вшивков

Пермь-2013

Приложение B

Применение MS Excel при решении задач оптимизации (поиск решения)

Дата добавления: 2014-12-07