Теорема Жуковского о подъемной силе одиночного профиля

Для определения сил взаимодействия лопастей с обтекающим решетку потоком полезно рассмотреть простой случай обтекания одиночного профиля плоскопараллельным потоком идеальной жидкости. На рис. 14.1 представлена схема обтекания пластины длиной L потоком жидкости со скоростью W ₀ и плотностью ρ. Равнодействующая распределенных по пластине единичной ширины сил давления - F, отклоняющих поток от направления W ₀ к W ₁, представлена как сумма проекций на оси х и у. Массовый расход М частиц, подвергающихся возмущению, определяется углом атаки γ:

М = ρ W ₀ 1 L Sin γ. (14.1)

Применение теоремы об изменении количества движения системы материальных точек (теоремы импульсов) дает возможность рассчитать величины F_Х и F _У:

_- проекция на ось х: МW ₁ Cos γ - М W ₀ = - F _Х,

- проекция на ось у: МW ₁ Sin γ -0 = F _У.

Полагая в первом приближении равенство скоростей W ₁ и W ₀ имеем:

F _Х = ρ W²₀ 1 L (1- Cos γ) Sin γ, (14.2)

F _У = ρ W²₀ 1 L Sin ² γ. (14.3)

Существенные качественные и количественные отклонения результатов расчета по 14.2 и 14.3 от измеряемых значений F_Х и F _У снимаются введением в эти формулы опытных аэродинамических коэффициентов С_Х (W₀ , γ) и С_У (W₀ , γ). Таким образом, вышеизложенная методика дает только набор параметров, описывающих процесс, и в некоторой степени структуру расчетных зависимостей. Основные причины несоответствия очевидны и вытекают из неверного представления о текучей среде как совокупности невзаимодействующих между собой частиц. Действительно, в создании подъемной силы F _У и силы лобового сопротивления F _Х участвуют не только верхняя, но и нижняя поверхность, а равенство скоростей W ₁ и W ₀ неочевидно, расчет М по формуле 14.1 вызывает сомнения и т.д. Кроме этого методика расчета не объясняет наличия F _У в случае горизонтального, выпуклого сверху профиля типа крыла птиц, когда Sin γ= 0.

Следуя Жуковскому, рассмотрим задачу обтекания профиля в более корректной постановке, изображенной на рис. 14.2. Возмущающая поток сила F распространяет свое влияние на массу жидкости, заключенную внутри контрольной поверхности радиуса r, ограниченной единичной длиной в направлении оси z, совпадающей с осью профиля. На выделенный объем жидкости кроме силы F оказывают силовое воздействие распределенные по цилиндрической поверхности силы давления окружающей среды.

М

При произвольном значении угла α выделим элементарную площадку dl=r d α, на которую действует зависящее от α давление Р( α), а скорость возмущенного потока в центре площадки обозначим вектором W (α).

		V (α)
		U (α)

		Рис. 14.2.

Проекции на оси x и у всех сил, действующих на выделенную массу, записываются при интегрировании распределенных сил давления:

- F _Х - , (14.4)

F _y - 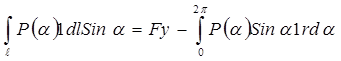, ( 14.5)

Проекции изменений количества движения на оси х и у вычисляются интегрированием по углу α от 0 до 2π произведения скоростей U (α) или V (α) на элементарный расход dM (α) через выделенное живое сечение 1 dl на контрольной поверхности:

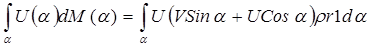, (14.6)

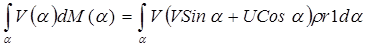. (14.7)

Для вычисления подъемной силы F_У используем теорему импульсов приравняем 14.5 к 14.7 и учтем, что при любых α V ² = W ^{2 –} U ²:

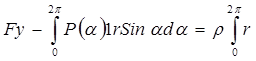1 (V² Sin α + UV Cos α) d α=

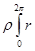= 1(W²Sin α – U ² Sin α + UVCos α) d α= 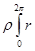1 W²Sin α d α + 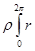1(UVCos α– U ² Sin α )d α=

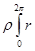= 1 W²Sin α d α + 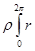1 U (VCos α– U Sin α )d α= 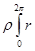1 W²Sin α d α + 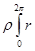1 UW _τ d α. (14.8)

В соотношении 14.8 W _τ(α)=(Vcos α – USin α ) –проекция скорости потока на касательную к цилиндрической контрольной поверхности.

Выполним анализ 14.8, учитывая произвольность величины r, который можно принять достаточно большим. При таком допущении возмущениями потока на контрольной поверхности можно пренебречь, т.е. в интегралах левой и правой частях положить Р (α)= Р ₀= Const и U (α)→ W (α)→ W ₀≈ Const. Это приводит к нулевым значениям интеграла правой части 14.8 и первого слагаемого левой. В результате расчет F _У сводится к вычислению интеграла:

F _У = 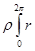1 UW τ d α. =1 W ₀ 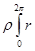W_τ(α)τ d α =1ρ W ₀ 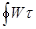(α) dl =1ρ W ₀ Г. (14.9)

Из формулы Жуковского следует, что если при обтекании профиля возникает циркуляция вектора скорости по замкнутому контуру – Г (гамма), то в создании подъемной силы участвуют большие массы жидкости в окрестностях профиля. Сила действия потока на профиль равна F _У и противоположна ей по направлению.

Для формирования Г при обтекании цилиндра радиусом R достаточно цилиндр вращать c угловой скоростью ω. Возникающая в этом случае подъемная сила, приложенная к цилиндру, (эффект Магнуса) соответствует величине Г=2π R ω (рис. 14.3, а). Обтекание несимметричного крылового профиля формирует подъемную силу F _У даже при нулевых углах атаки за счет более высоких скоростей течения на выпуклой стороной профиля по сравнению с плоской нижней. В этом случае можно иметь высокое значение F _У при минимальном лобовом сопротивлениии F _Х.

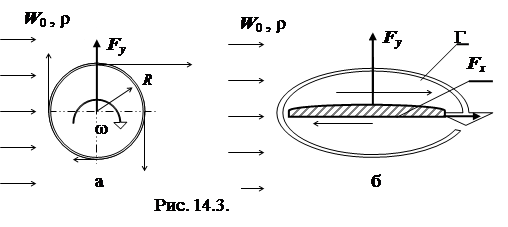
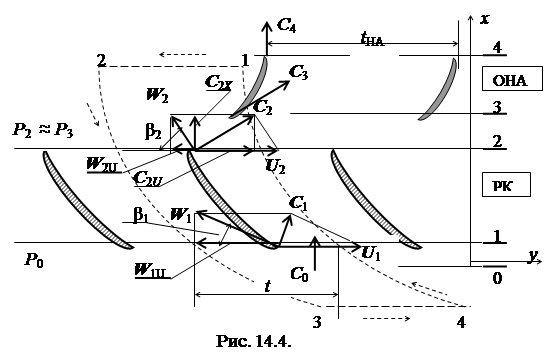
Применительно к течению в решетке профилей осевого насоса (см. рис. 14.4) для каждой лопасти циркуляция вектора скорости Г, т.е. интеграл по контуру 1-2-3-4 легко вычисляется по известному шагу t и величинам W ₂ u, W ₁ u. При обходе лопасти, как указано на рисунке стрелками, величина Г складывается из двух слагаемых, соответствующих участкам 1-2 и 3-4:

Г= t W ₂ u - t W ₁ u = t (W ₂ u - W ₁ u) (14,10)

Расчет циркуляции для лопасти направляющего аппарата дает величину циркуляции:

Г_НА= t _НА С _{4 У} + t _НА С _{3 У} = t _НА С _{3 У} . (14,11)

Теорема Жуковского служит теоретической базой для инженерных методик расчета осевых насосов. При этом широко использоваются экспериментальные данные полученные на испытаниях насосных агрегатов и продувке решеток.

Дата добавления: 2014-12-07