Количественная оценка информации

3.1 Энтропия, как мера неопределенности выбора независимых сообщений дискретного источника [1,2,3,4 и др.].

В данном разделе ставятся задачи установления количественных мер неопределенности и информации и выяснения их основных свойств для дискретного источника.

Начнем рассмотрение с источника информации, который может в каждый момент времени случайным образом принять одно из конечного множества возможных состояний. Такой источник называют дискретным источником информации. При этом принято говорить, что различные состояния реализуются вследствие выбора их источником. Каждому состоянию источника x ставится в соответствие условное обозначение в виде знака (в частности, буквы) из алфавита данного источника: x₁, x₂, …, x_N.

Для получения результата выбора источником конкретного состояния x можно высказать ряд предположений, базирующихся на априорных сведениях об источнике информации. Поскольку одни состояния выбираются источником чаще, а другие реже, то в общем случае он характеризуется ансамблем X, т.е. полной совокупностью состояний с вероятностями их появления, составляющими в сумме единицу:

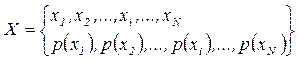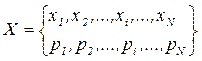или (3.1)

причем

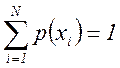или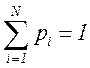

Обе формы записи используются в дальнейшем на равных основаниях.

Опираясь на эти сведения, введем сначала меру неопределенности выбора состояния источника. Ее можно рассматривать и как меру количества информации, получаемой при полном устранении неопределенности относительно состояния источника. Мера должна удовлетворять ряду естественных условий. Одним из них является необходимость выбора, т.е. числа возможных состояний источника N, причем недопустимые состояния (состояниями с вероятностями, равными нулю) не должны учитываться, так как они не меняют неопределенности.

Ограничиваясь только этим условием, за меру неопределенности можно было бы взять число состояний, предположив, что они равновероятны. Однако такая мера противоречит некоторым интуитивным представлениям. Например, при N=1, когда неопределенность отсутствует, она давала бы значение, равное единице. Кроме того, такая мера не отвечает требованию аддитивности, состоящему в следующем.

Если два независимых источника с числом равновероятных состояний N и M рассматривать как один источник, одновременно реализующий пары состояний n_im_j, то естественно предположить, что неопределенность объединенного источника должна равняться сумме неопределенностей исходных источников. Поскольку общее число состояний объединенного источника равно NM, то искомая функция должна удовлетворять условию

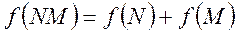(3.2)

Соотношение (3.2) выполняется, если в качестве меры неопределенности источника с равновесными состояниями и характеризующего его ансамбля x принять логарифм числа состояний:

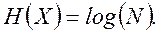(3.3)

Тогда при X=1 H(X)=0 и требование аддитивности выполняется.

Указанная мера была предложена американским ученым Р. Хартли в 1928 г. Основание логарифма не имеет принципиального значения и определяет только масштаб или единицу неопределенности. Так как современная техника базируется на элементах, имеющих два устойчивых состояния, то обычно выбирают основание логарифма равным двум. При этом единица неопределенности называется двоичной единицей или битом и представляет собой неопределенность выбора из двух равновероятных событий (bit – сокращение от англ. binary digit – двоичная единица). Если основание логарифма выбрать равным десяти, то неопределенность получим в десятичных единицах на одно состояние (дитах).

Однако ясно, что такая оценка меры неопределенности учитывает не все априорные сведения, характеризующие опыт X. В этой оценке меры неопределенности не учтены вероятности различных исходов.

Дальнейшее развитие понятия неопределенности получило в работах К. Шеннона. Он ограничил рамки применимости формул Хартли лишь случаем, когда все N исходов в опыте X равновероятны. В этом случае вероятность любого исхода p_i=1/N и формулу (3.3) можно переписать в виде

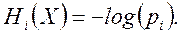(3.4)

Формула показывает, что неопределенность исхода зависти от вероятности исхода. К. Шеннон применил эту формулу к разновероятным исходам, усреднив затем полученные неопределенности по всем исходам. Для опыта X={x₁, …, x_m}, где x₁, …, x_m – возможные исходы с вероятностями p₁, …, p_m, неопределенность каждого исхода –log(p₁), -log(p₂), …, -log(p_m), а математическое ожидание

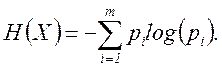(3.5)

Дата добавления: 2014-12-07