Формулы оценивания при гнездовом отборе

Статистические показатели	Истинное значение	Оценка
Суммарное значение признака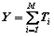
Среднее значение признака по гнездам
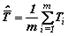
Среднее значение признака
Дисперсия оценки суммарного значения признака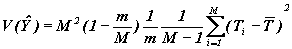
Дисперсия оценки среднего значения признака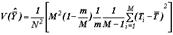
Стандартная ошибка оценки суммарного значения признака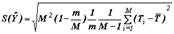
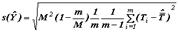
Стандартная ошибка оценки среднего значения признака
Коэффициент вариации оценки

В таблице 4 использованы следующие обозначения:

i	-	номер гнезда;
M	-	количество гнезд;
Ti	-	суммарное значение признака в i -м гнезде;
m	-	количество выбранных гнезд;
N	-	объем генеральной совокупности;
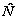
	-	оценка объема генеральной совокупности.

Систематический (механический) отбор. Для осуществления систематического отбора все единицы совокупности нумеруются в некотором порядке числами от 1 до N. Для получения выборки объемом n единиц сначала извлекается, например, случайным образом какая-либо единица из первых k = N/n единиц совокупности. После этого в выборку включается каждая k -я единица, начиная с уже извлеченной. Извлечение первой единицы определяет всю выборку. Такая выборка называется систематической выборкой каждой k -й единицы. Отношение N/n называется интервалом или шагом отбора.

В отдельных случаях при наличии соответствующей информационной базы для повышения точности выборочных результатов единицы генеральной совокупности предварительно ранжируются по какому-либо существенному признаку. При таком подходе отбор единиц в выборочную совокупность начинается с единицы, находящейся в середине первого интервала.

В теории систематический отбор считается более эффективным, чем простая случайная выборка. Также его легче осуществлять при работе вручную, что потеряло актуальность с широким распространением персональных компьютеров. Следует отметить два недостатка этого способа отбора:

затруднено получение несмещенной оценки выборочной дисперсии;

существуют такие совокупности и значения n, при которых простая случайная выборка дает более точные оценки показателей (дисперсия оценки среднего систематической выборки для этих совокупностей может даже расти при увеличении объема выборки). Наличие периодического или циклического изменения в значениях признака, период которого равен интервалу отбора, - наихудшая из возможных ситуаций при систематическом отборе.

При систематическом отборе обычно применяются оценочные формулы простого случайного отбора, так как систематический отбор можно рассматривать как простой случайный, содержащий одну гнездовую единицу из совокупности k гнездовых единиц.

Дисперсия среднего значения при систематическом отборе определяется по формуле:

,

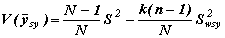где	N	-	объем генеральной совокупности;
	S^2	-	истинное значение дисперсии признака;
	k	-	шаг отбора;
	n	-	объем выборочной совокупности;
	S^2wsy	-	дисперсия единиц, принадлежащих одной и той же систематической выборке (wsy - от английского "within" - внутри и "systematic" - систематический):

;

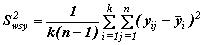	yij	-	значение признака j -го члена i -й систематической выборки, j = 1, 2,..., n, i = 1, 2,...,k;
		-	среднее значение признака i -й выборки.

Многоступенчатый или многошаговый отбор (подвыборки). При организации статистических выборочных обследований широко применяется метод многоступенчатого отбора. Если исследуемая совокупность содержит некоторые группы и имеется информация о принадлежности элементов к той или иной группе, то в этом случае при выборочных обследованиях может быть удобным вначале осуществить случайную выборку из этих групп, а затем в целях экономии средств и времени не проводить обследование всех единиц отобранных групп, как при гнездовом отборе, а отобрать лишь часть элементов в каждой выбранной группе, т.е. осуществить двухступенчатый отбор. При многоступенчатом отборе извлечение единиц наблюдения осуществляется после нескольких последовательных случайных отборов групп.

В качестве примера многоступенчатого отбора рассмотрим его специальный случай - двухэтапный групповой отбор, в котором элементы второго этапа - единицы наблюдения, случайным образом отобранные из элементарных единиц выбранных групп.

Таблица 5

Дата добавления: 2014-12-07