Підсилювальна ланка

Вступ.

Доведення теми лекції, її ролі у системі підготовки військового фахівця, цільової настанови та плану лекції.

Стисла характеристика літератури, що рекомендується.

1. Поняття елементарної ланки.

Передаточна функція лінійної неперервної стаціонарної САК може бути представлена у вигляді відношення многочленів відносно змінної Лапласа p:

. (1)

В силу теореми Безу многочлени і 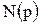можуть бути представлені таким чином

, (2)

, (3)

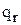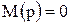де , – корені рівнянь та 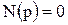відповідно.

Виділимо в кожному многочлені три групи співмножників, виходячи з того, що корені рівнянь можуть бути нульовими, дійсними (відмінними від нуля) і комплексними, та перетворимо їх до деякого типового вигляду. Міркування проведемо для многочлена 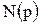, що стоїть у знаменнику.

Якщо 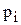– нульовий корінь, то .

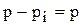Якщо 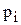– дійсний корінь, відмінний від нуля, то відповідний співмножник можна представити у вигляді

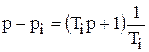, (4)

де

. (5)

Якщо – комплексний корінь, то завжди є комплексно спряжений корінь 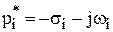, і добуток відповідних їм співмножників є многочленом другого степеня, який можна представити таким чином

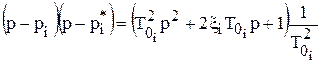, (6)

де

, (7)

. (8)

Аналогічно три типи співмножників можна виділити у многочлені , що стоїть у чисельнику передаточної функції.

Припустимо, що в чисельнику і знаменнику є 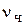і нульових коренів, і 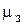дійсних відмінних від нуля коренів, і пар комплексно сполучених коренів відповідно. Тоді, як випливає з викладеного вище, передаточна функція системи може бути представлена у вигляді

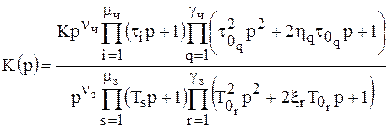, (9)

де K – числовий коефіцієнт;

,

.

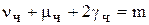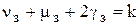Таким чином, передаточна функція лінійної неперервної стаціонарної САК може бути представлена як добуток сьомі типів співмножників: K, , , , , , .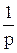

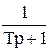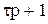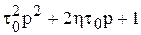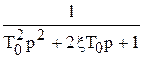Відзначимо, що в кожному з співмножників допускають наявність деякого чисельного множника K.

Типові співмножники передаточної функції лінійної неперервної стаціонарної САК називаються елементарними ланками. Назви елементарних ланок та їх передатні функції наведені в перших двох рядках табл. 1 – 3 на обкладинках навчального посібника. При введенні елементарних ланок вважають, що їх параметри задовольняють нерівностям 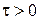, , 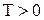, , 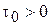, 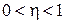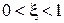. Далі в п. 4.2 – 4.9 розглядаються основні характеристики елементарних ланок.

2. Характеристики підсилюючої, інтегруючої та диференціюючої ланок.

Підсилювальною називається ланка, яка має таку передаточну функцію

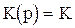. (10)

Ця ланка має один параметр K, який називають коефіцієнтом підсилення ланки.

По передаточній функції підсилювальної ланки знайдемо її оператор передачі шляхом формальної заміни змінної Лапласа p на символ диференціювання D:

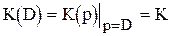. (11)

Оскільки зв'язок між вхідним і вихідним діяннями в часовій області задається оператором передачі, підсилювальна ланка описується рівнянням “вхід-вихід”

, (12)

з якого випливає, що в залежності від фізичної природи вхідного та вихідного діянь коефіцієнт підсилення підсилювальної ланки може мати різну розмірність

.

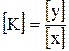Відповідно до рівняння “вхід-вихід” (12) підсилювальна ланка є безінерційною, оскільки поточне значення її реакції визначається лише значенням коефіцієнта підсилення ланки та поточним значенням вхідного діяння та не залежить від передісторії руху ланки (процесів, що протікали у ланці до поточного моменту часу). Тому підсилювальну ланку часто називають безінерційною.

Комплексна частотна характеристика підсилювальної ланки може бути знайдена по передаточній функції чи оператору передачі шляхом відповідної формальної заміни

. (13)

Як випливає з виразу (13), АЧХ і ФЧХ підсилювальної ланки визначаються виразами[1]

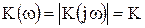, (14)

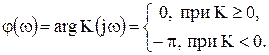(15)

Їх графіки наведені на рис. 1.

ЛАЧХ підсилювальної ланки випливає з виразу (14)

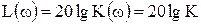(16)

і являє собою пряму, що проходить через точку з координатами паралельно осі абсцис.

ЛФЧХ підсилювальної ланки визначається виразом (15), але розглядається як функція логарифма частоти.

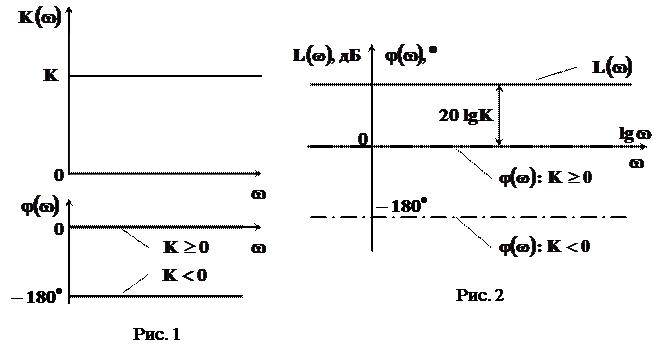Графіки ЛАЧХ і ЛФЧХ підсилювальної ланки наведені на рис. 2 суцільною та штрихпунктирною лініями відповідно.

З виразу (12) випливає, що імпульсна і перехідна характеристики підсилювальної ланки визначаються виразами

, (17)

, (18)

тобто їх графіки повторюють відповідні вхідні діяння з масштабним коефіцієнтом K (рис. 3, 4).

Характеристики підсилювальної ланки зведені у другому стовпці табл. 1.

2.2. Інтегруюча ланка.

Інтегруючою називається ланка, яка має таку передаточну функцію

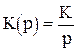. (19)

Ця ланка має один параметр K, який називають коефіцієнтом підсилення ланки.

По передаточній функції інтегруючої ланки знайдемо її оператор передачі шляхом формальної заміни p на D:

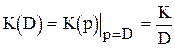. (20)

За допомогою оператора передачі визначається зв'язок між вхідним і вихідним діяннями в часовій області

, (21)

звідки випливає, що інтегруюча ланка описується таким диференціальним рівнянням “вхід-вихід”

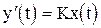. (22)

Таким чином, швидкість зміни вихідного діяння інтегруючої ланки пропорційна вхідному діянню, тому розмірність коефіцієнта підсилення інтегруючої ланки зворотно пропорційна одиниці вимірювання часу – секунді:

.

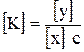Проінтегрував вираз (22), можна показати, що вихідне діяння інтегруючої ланки являє собою інтеграл від вхідного діяння

, (23)

де – початкова умова при інтегруванні.

Вираз (23) пояснює назву ланки – інтегруюча. З нього також випливає, що при закінченні вхідного діяння інтегруючої ланки її вихідне діяння фіксується на рівні, на якому воно було в момент закінчення вхідного діяння. Ця властивість інтегруючої ланки називається властивістю “пам’яті”.

Комплексна частотна характеристика інтегруючої ланки може бути знайдена по передаточній функції чи оператору передачі шляхом відповідної формальної заміни

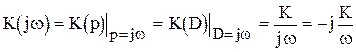. (24)

Як випливає з виразу (24), АЧХ і ФЧХ інтегруючої ланки визначаються виразами

, (25)

. (26)

Їх графіки наведені на рис. 5.

ЛАЧХ інтегруючої ланки випливає з виразу (25)

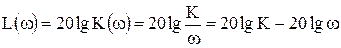. (27)

Оскільки ЛАЧХ будується як функція , вона є лінійною залежністю, тобто являє собою пряму, що проходить через точку з координатами з нахилом

.

Ще одна характерна точка, через яку проходить ЛАЧХ інтегруючої ланки, має координати .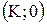

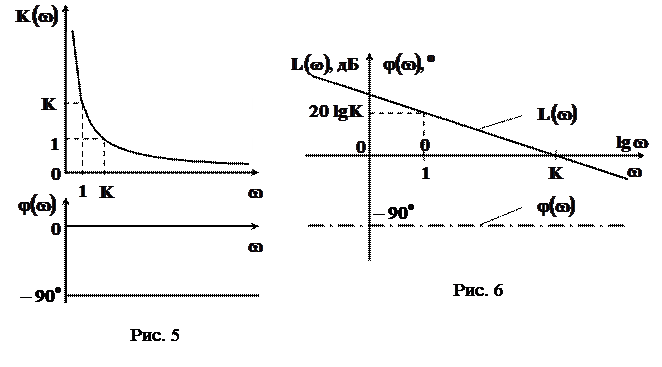ЛФЧХ інтегруючої ланки визначається виразом (26), але розглядається як функція логарифма частоти.

Графіки ЛАЧХ і ЛФЧХ інтегруючої ланки наведені на рис. 6 суцільною та штрихпунктирною лініями відповідно.

По передаточній функції інтегруючої ланки знаходять її імпульсну і перехідну характеристики

, (28)

. (29)

Графіки часових характеристик інтегруючої ланки наведені на рис. 7, 8.

Характеристики інтегруючої ланки зведені у третьому стовпці табл. 1.

Дата добавления: 2014-12-07