
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы комбинаторики. 2 страница
|
|
|
|
ЗАДАЧА. Вероятность того, что зашедший в ресторан посетитель сделает заказ равна 0,8. Определить вероятность того, что из 100 зашедших не менее 75 сделают заказ.
РЕШЕНИЕ.
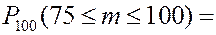
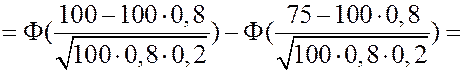

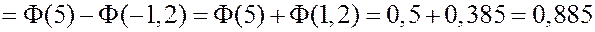
Закон редких явлений Пуассона.
Если вероятность появления события  мала
мала 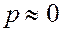 , а число испытаний велико
, а число испытаний велико 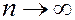 , то для приближенного вычисления
, то для приближенного вычисления 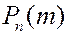 используем закон Пуассона. Положим
используем закон Пуассона. Положим 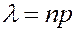 . Тогда
. Тогда
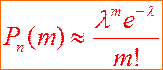
Закон Пуассона дает хорошее приближение при 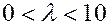 .
.
ЗАДАЧА. Завод отправил на базу партию в 500 изделий. Вероятность повреждения в пути 0,002. Найти вероятность прибытия не более трех негодных изделий.
РЕШЕНИЕ. 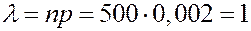
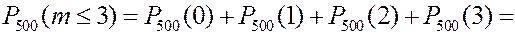
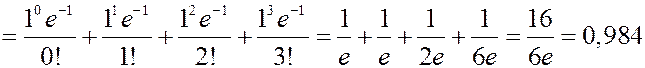 Сравним с точным значением:
Сравним с точным значением:
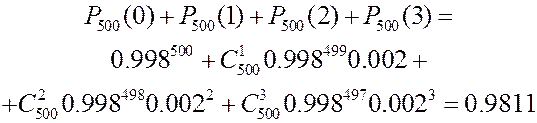
Случайные величины.
Случайная величина – это величина, которая в результате опыта может принять то или иное значение случайным образом с некоторой вероятностью.
Случайные величины могут быть дискретными и непрерывными.
Дискретная случайная величина – это величина, число возможных значений которой конечно или счётно. Например, число попаданий при трех выстрелах(0,1,2,3) или число вызовов, поступивших на телефонную станцию за сутки (0,1,2,3,4,…).
Непрерывная случайная величина – величина, возможные значения которой непрерывно заполняют некоторый промежуток. Например, вес наугад взятого зерна пшеницы или скорость самолета в момент выхода на заданную высоту.
Случайные величины обозначают 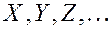 , а значения случайных величин
, а значения случайных величин 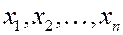 .
.
Закон распределения случайной величины – это всякое соответствие, устанавливающее связь между значениями случайной величины и соответствующими вероятностями.
Дискретные случайные величины.
Рассмотрим дискретную случайную величину (ДСВ)  с возможными значениями
с возможными значениями 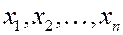 . Каждое значение возможно, но не достоверно. Величина
. Каждое значение возможно, но не достоверно. Величина  может принять каждое значение с некоторой вероятностью.
может принять каждое значение с некоторой вероятностью.
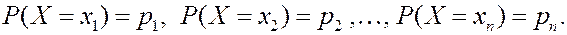
В результате опыта ДСВ  примет одно из этих значений, которые несовместны и образуют полную группу.
примет одно из этих значений, которые несовместны и образуют полную группу.
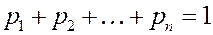
Простейшая форма задания значений случайной величины и соответствующих вероятностей – это таблица, которая называется ряд распределения ДСВ  .
.
| X | 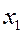
| 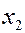
| ¼ | 
|
| p | 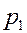
| 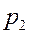
| ¼ | 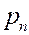
|
Для наглядности можно по оси абсцисс отложить значения случайной величины, а по оси ординат соответствующие вероятности и соединить полученные точки.
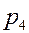
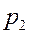
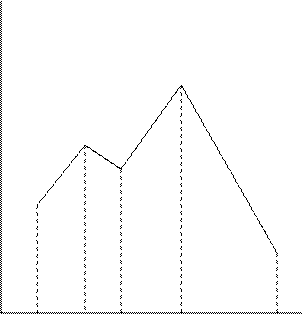
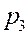
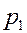
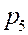
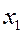
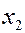
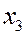
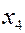

ЗАДАЧА. Вероятность того, что необходимая студенту книга свободна 0,7. Составить закон распределения числа библиотек, которые посетит студент, если всего в городе их четыре.
РЕШЕНИЕ. 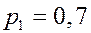 ,
, 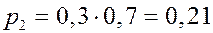
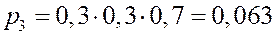 ,
, 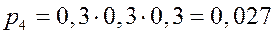
| X | ||||
| P | 0.7 | 0,21 | 0,063 | 0,027 |
Числовые характеристики дискретных
случайных величин.
Математическое ожидание.
Математическое ожидание ДСВ – число равное сумме произведений значений случайной величины на соответствующие вероятности.

| 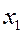
| 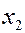
| 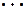
| 
|
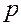
| 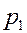
| 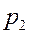
| 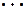 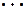
| 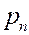
|
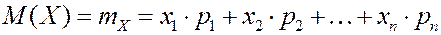
Свойства математического ожидания.
1. Математическое ожидание от постоянной величины равно самой этой величине. 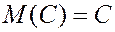
2. Математическое ожидание от мат. ожидания равно мат. ожиданию. 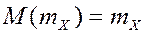
3. Постоянную можно вынести за знак математического ожидания. 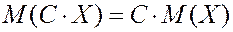
4. Математическое ожидание суммы двух случайных величин равно сумме мат. ожиданий этих случайных величин. 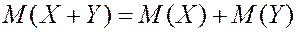
5. Математическое ожидание произведения двух независимых величин равно произведению мат. ожиданий. 
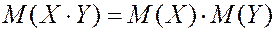
ЗАДАЧА. Найти мат. ожидание суммы очков при подбрасывании двух игральных костей.
РЕШЕНИЕ. Первый способ. Пусть  - сумма очков на двух костях.
- сумма очков на двух костях.

| |||||||||||
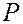
| 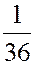
| 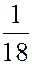
| 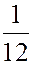
| 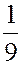
| 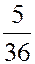
| 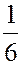
| 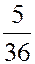
| 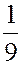
| 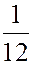
| 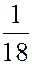
| 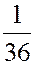
|
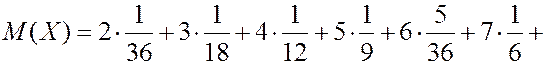
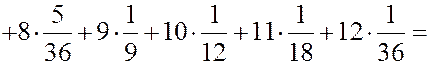
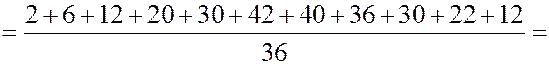
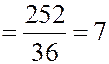
Второй способ. Пусть  - число очков на первом игральном кубике,
- число очков на первом игральном кубике,  - число очков на втором.
- число очков на втором.

| ||||||
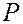
| 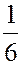
| 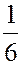
| 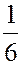
| 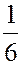
| 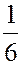
| 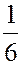
|
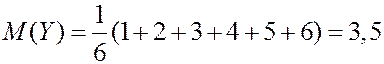

| ||||||
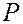
| 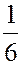
| 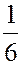
| 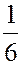
| 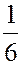
| 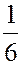
| 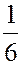
|
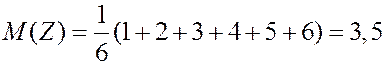
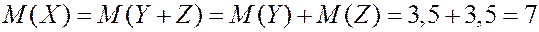
Мода.
Мода дискретной случайной величины – это то её значение, которому соответствует большая вероятность.
В задаче 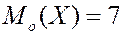 .
.
ПРИМЕР.

| |||
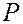
| 0,3 | 0,5 | 0,2 |
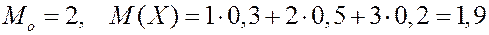
Медиана.
Медиана – то значение случ. величины, для которой выполняется условие: 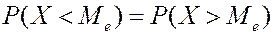
ПРИМЕР.

| ||||||
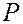
| 0,2 | 0,2 | 0,2 | 0,1 | 0,2 | 0,1 |
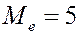
Дисперсия.
Рассмотрим случайную величину 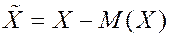
(центрированная случайная величина). Для нее имеем:
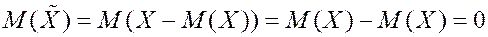
Определение. Дисперсия сл. величины  есть мат. ожидание квадрата случ. величины
есть мат. ожидание квадрата случ. величины 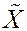 , то есть
, то есть
 Û
Û 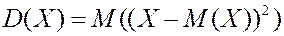
Закон распределения 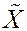 имеет вид
имеет вид
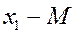
| 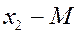
| 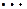
| 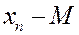
|
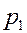
| 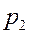
| 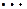
| 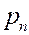
|
Для 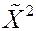 , следовательно, получаем
, следовательно, получаем
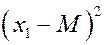
| 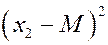
| 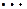
| 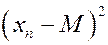
|
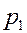
| 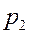
| 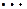
| 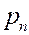
|
Поэтому 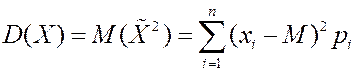
Свойства дисперсии.
1) Если 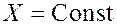 , то
, то 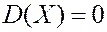 :
:
2) Для произвольной константы 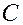
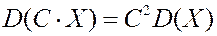
3) Для суммы независимых случайных величин  и
и 
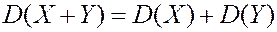
4) Для произвольной с.в.  имеет место соотношение
имеет место соотношение
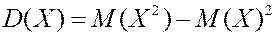
Пример. Найти дисперсию дискретной с.в., заданной законом распределения

| |||
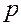
| 0.3 | 0.2 | 0.5 |
Решение.
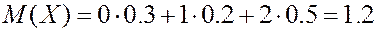
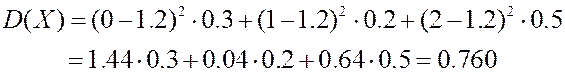
Если использовать вторую формулу, получим
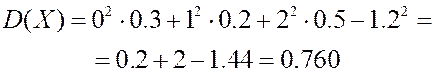
Среднее квадратичное отклонение.
Устраняет разницу в единицах измерения между математическим ожиданием и дисперсией.
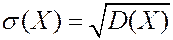
Интегральная функция распределения вероятности.
Пусть задана случайная величина  и
и  - любое действительное число. Вероятность того, что случайная величина
- любое действительное число. Вероятность того, что случайная величина  примет значение меньше
примет значение меньше  называется интегральной функцией распределения СВ
называется интегральной функцией распределения СВ  .
.
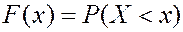
Свойства.
1. Значения интегральной функции удовлетворяют неравенству 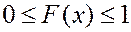 .
.
2. Интегральная функция 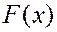 является неубывающей функцией.
является неубывающей функцией.
3. Вероятность того, что случайная величина примет значение из интервала 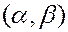 , равно приращению интегральной функции на этом интервале.
, равно приращению интегральной функции на этом интервале.

4. Если все значения случайной величины принадлежат интервалу 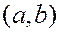 , то интегральная функция
, то интегральная функция
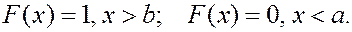
5. 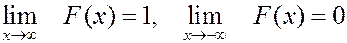
ПРИМЕР. Построить интегральную функцию распределения для случайной величины, заданной рядом распределения.

| ||||
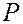
| 0.2 | 0.3 | 0.4 | 0.1 |
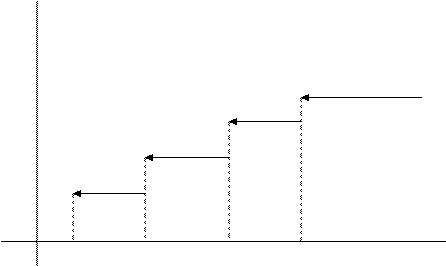
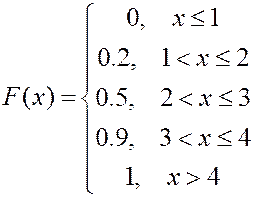
0.9
0.5
0.2
1 2 3 4
Непрерывные случайные величины.
Вероятность попадания НСВ в точку равна 0.
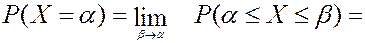
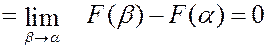
Вероятности того, что НСВ будет принимать значения на отрезке 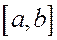 и на интервале
и на интервале 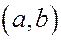 , одинаковы.
, одинаковы.
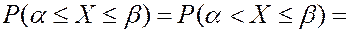
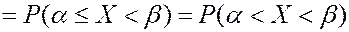
Дифференциальная функция распределения
(плотность вероятности).
Пусть функция 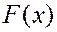 непрерывна и дифференцируема. Тогда первая производная интегральной функции и называется дифференциальной функцией.
непрерывна и дифференцируема. Тогда первая производная интегральной функции и называется дифференциальной функцией.
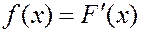
Свойства.
1. Дифференциальная функция неотрицательна.
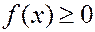 так как
так как 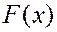 неубывающая.
неубывающая.
2. Вероятность попадания случайной величины в промежуток равна интегралу от диф. функции по этому промежутку.
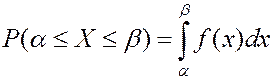
3. 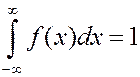
4. Интегральную функцию можно найти, если взять интеграл с переменным верхним пределом от дифференциальной функции.
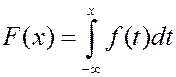
ПРИМЕР. СВ  распределена с плотностью
распределена с плотностью
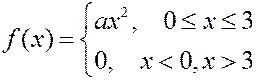

Найти:
1) параметр 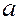 ,
,
2) интегр. функцию 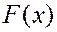 ,
,
3) вероятность того, что случайная величина примет значение в промежутке 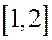 ,
,
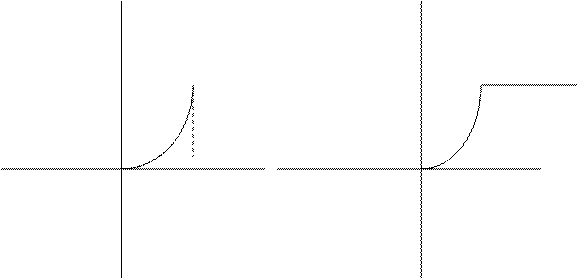
4) построить графики функций 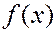 и
и 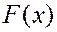 .
.
РЕШЕНИЕ. 1) 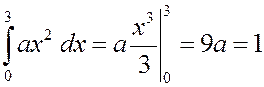
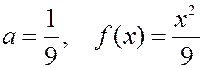
 2) При
2) При 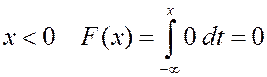 ,
,
при 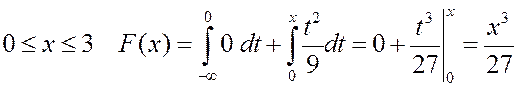 ,
,
при 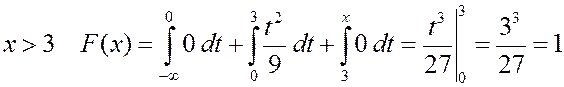 .
.
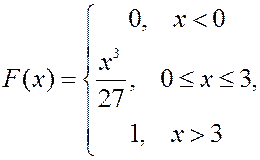
3) 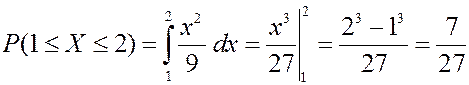
 4)
4) 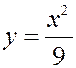
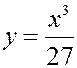
1 1
0 3  0 3
0 3 
Математическое ожидание и дисперсия
непрерывных случайных величин.
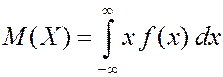
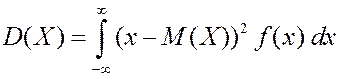
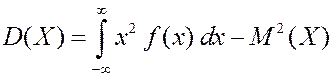
ПРИМЕР. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение для случайной величины, заданной плотностью вероятности из предыдущей задачи.
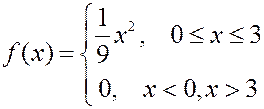
Решение. Найдем мат. ожидание как определенный интеграл в пределах от 0 до 3, так как вне этого интервала 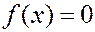 .
.
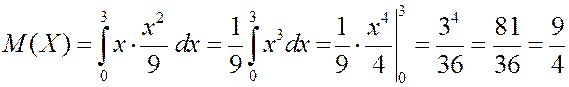
Теперь найдем дисперсию случайной величины.
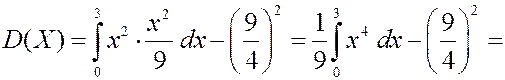
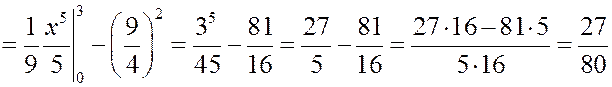
Найдем среднее квадратичное отклонение.
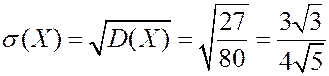
ЗАДАЧА. НСВ  задана интегральной функцией распределения вероятностей.
задана интегральной функцией распределения вероятностей.
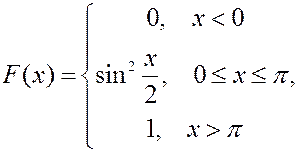
Найти плотность вероятности, построить графики функций 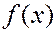 и
и 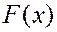 , вычислить мат. ожидание и дисперсию, найти вероятность попадания СВ в промежуток
, вычислить мат. ожидание и дисперсию, найти вероятность попадания СВ в промежуток 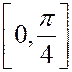 .
.
Решение. Найдем плотность вероятности. 
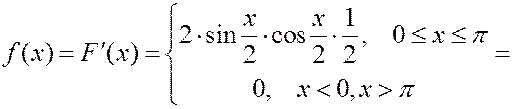
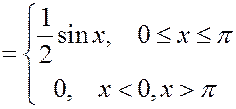
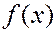
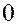
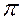
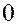
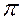
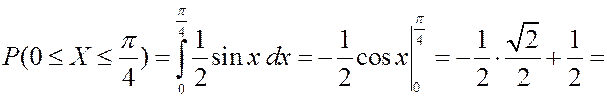
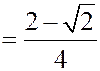
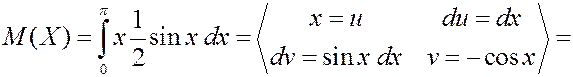
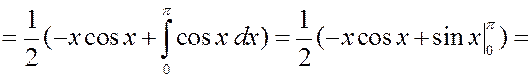
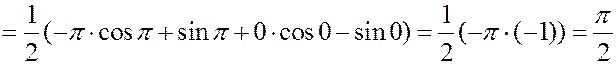
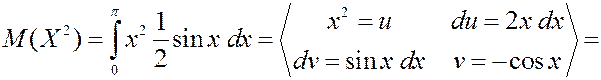
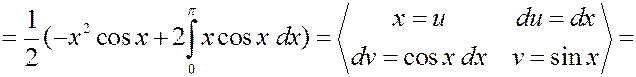
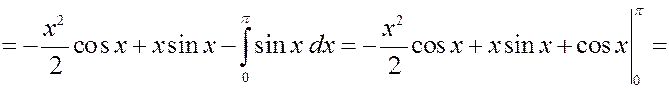
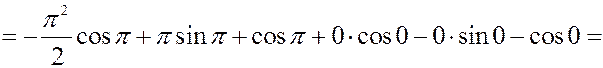
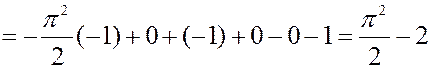
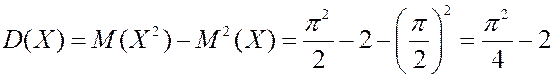
Равномерное распределение.
Пусть плотность вероятности является постоянной. 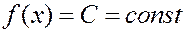 на интервале
на интервале 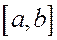 и
и 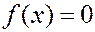 вне этого интервала.
вне этого интервала.
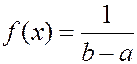
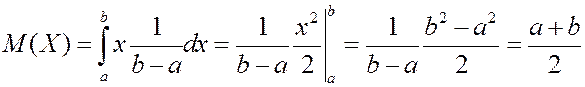
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 461; Нарушение авторских прав?; Мы поможем в написании вашей работы!