Свойства проецирования

Основные разделы инженерной графики

Инженерная графика

Разделы: 1.Начертательная геометрия   2.Техническое черчение   3. Компьютерная графика

Задачи: Метод проекций. Решение пространственных задач (метрических и позиционных). Способы построения и чтения чертежей. Законы построения чертежей (ГОСТы ЕСКД, ЕСПДС и др.) Графические пакеты

Начертательная геометрия - это раздел математики, в геометрии изучающий теорию методов отображения пространств различных структур и размерностей друг на друга (пространства Евклида, Лобачевского, Римана, в том числе и многомерные). Основным методом начертательной геометрии является метод проекций или отображений.

Использование разнообразных групп преобразований лежит в основе построения различных геометрий:

- топологические преобразования (многопараметрические);

- бирациональные (проецирование косыми лучами);

- проективные (центральное проецирование, проективная геометрия);

- аффинные (параллельное проецирование, аффинная геометрия);

- движение (геометрия Евклида).

Наше изучение будет ограничено аффинными преобразованиями в трех­мер­ной геометрии Евклида, т.е. частью начертательной геометрии, необходимой для построения и чтения технических чертежей изделий. Ее основоположником является французский геометр и инженер XVIII века Гаспар Монж, который сказал: "Чертеж-язык техники², а русский геометр и инженер XX века Курдюмов С.П. добавил: ²Начертательная геометрия - грамматика чертежа².

Основу "Начертательной геометрии" составляет элементарная геометрия - наука, изучающая пространственные формы тел и их отношения. К основным формообразующим элементам пространства относятся точка, прямая, плоскость. Ими определяются простые трехмерные фигуры, из которых создаются сложные объекты. В начертательной геометрии принято точки обозначать прописными буквами А,В,С,... или арабс­ки­ми цифрами 1, 2, 3...; прямые - строчными буквами латинского алфавита: а,в,с,...; плоскости - прописными буквами греческого алфавита: G, L, P, S, F, Y, W.

В начертательной геометрии решаются два основных вида задач:

1) Позиционные задачи - на взаимное расположение геометрических элементов.

2) Метрические задачи - на определение натуральных величин расстояний или углов между геометрическими фигурами, определение истинных размеров геометр. фигур (отрезков, треугольников, многоугольников и т.п.).

Метод начертательной геометрии - метод проекций. Аппарат проецирования включает в себя проецирующие лучи, проецируемый объект (оригинал или прообраз) и плоскость проекций, на которой получается изображение объекта (проекция оригинала или образ) (рис.1.1).

Различают три вида проецирования: центральное (а), параллельное (б) и ортогональное (перпендикулярное) (в). При центральном проецировании все лучи выходят из одной точки S (например, фотографирование).

Если центр проекций S удален в бесконечность, то все лучи становятся параллельными - параллельное проецирование.

Частный случай параллельного проецирования - ортогональное проецирование, когда проецирующие лучи перпендикулярны плоскости проекций.

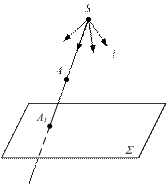
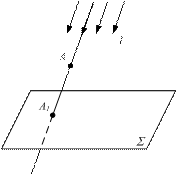
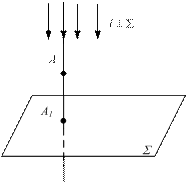
а) б) в)

Σ - плоскость проекций; l - проецирующий луч; А - оригинал;

А₁ - проекция оригинала или точка пересечения проецирующего луча с плоскостью

Рисунок 1.1

Все виды проецирования обладают следующими свойствами:

1) Проекция точки есть точка (исключение - центр проекций S).

2) Проекция прямой есть прямая; частный случай - точка, если направление прямой совпадет с направлением проецирующего луча.

3) Если точка принадлежит прямой, то и проекция точки принадлежит проекции этой прямой.

Параллельное и ортогональное проецирование обладает кроме этого дополнительными свойствами:

4) Если прямые параллельны, то и их проекции параллельны.

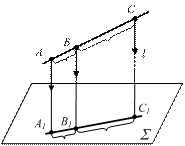
5) Сохраняется величина отношения длин отрезков, лежащих на одной пря­мой или на параллельных прямых (рис.1.2а).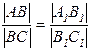

И, наконец, ортогональное проецирование обладает только ему присущими свойствами:

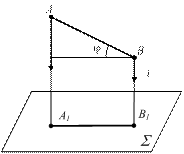
6) Для отрезка | АВ | и его ортогональной проекции | А₁В₁ | справедливо соотношение (рис.1.2б): | А₁В₁ ê=| АВ ê × соsj

где j - угол между отрезком и его ортогональной проекцией.

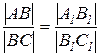
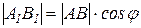
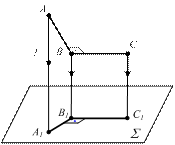
		ÐАВС=ÐА1В1С1=90°
а)	Б)	в)

Рисунок 1.2

7) Прямой угол проецируется в прямой угол, если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна (рис.1.2 в).

Метод ортогонального проецирования лежит в основе изучаемого нами раздела начертательной геометрии. Однако, полученное изображение на одной плоскости проекций не позволяет однозначно определить форму и размеры изображенного предмета (рис.1.3).

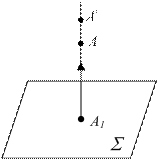
Рисунок 1.3

Дата добавления: 2014-12-07