КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачі розподілення ресурсів
|
|
|
|
Тема 2. Розподільчі задачі.
Розподільчі задачі – це розділ дослідження операцій, який вивчає оптимальний розподіл ресурсів за операціями, які необхідно виконувати з найбільшою сумарною ефективність.
Загальна постановка задач.
Нехай убудь-якій економічній системі є в наявності: m видів ресурсів, які можутьбути використані для здійснення n видів операцій (робіт).
Вважаємо, що будь-який ресурс може бути використаний для виконання будь-якої операції. Необхідно знайти такий розподіл ресурсів за операціями, при якому максимізується загальний прибуток від використання ресурсів, або результат, виражений в якійсь іншій формі, або мінімізуються загальні витрати ресурсів.
Розподільчу задачу легко представити у вигляді таблиці:
| Види ресурсів | Операція, яку необхідно виконати | ||||
| О1 | О2 | ... | Оn | Об’єм наявних ресурсів | |
| R1 | С11 | С12 | ... | С1n | b1 |
| R2 | С21 | С22 | ... | С2n | b2 |
 Rm Rm
| Сm1 | Сm2 | ... | Сmn | bm |
| Обсяг необхідних ресурсів | a1 | a2 | ... | am | Σ bm Σ am |


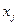 - обсяг виконаної роботи;
- обсяг виконаної роботи;
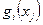 - функція витрат і- го виду ресурсу на j -тий тип операції.
- функція витрат і- го виду ресурсу на j -тий тип операції.
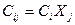
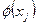 - результат від розподілу ресурсів за операціями.
- результат від розподілу ресурсів за операціями.
Іноді, економічно-математична модель в розподільчому виді має вигляд:
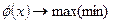
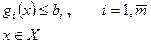
Математична модель розподільчої задачі в загальному випадку представляє собою задачу математичного програмування, тобто таку задачу, в котрій треба знайти екстремум функції при заданих обмеженнях на область допустимих значень змінних.
Класифікації розподільчих задач:
1) за визначеністю параметрів моделі:
- детерміновані;
- стохастичні;
2) за урахуванням фактору часу:
- статичні;
- динамічні;
3) за видом функцій 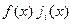 :
:
- лінійні;
- нелінійні;
4) за областю та множиною допустимих значень змінних:
- дискретні;
- неперервні ( );
);
5) за кількістю ресурсів:
- однопродуктові;
- багатопродуктові;
6) за сферою використання:
- виробничі;
- транспортні;
- призначення;
- розміщення;
- маршрутизації та ін.
7) задача формування виробничої програми підприємства.
Нехай на деякому підприємстві є m видів ресурсів, які використовуються для виробництва п видів продукції.
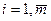 - види ресурсів;
- види ресурсів;
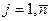 - види продукції.
- види продукції.
Відомі норми витрат на виготовлення одиниці продукції кожного виду
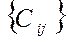 mxn
mxn
Для кожного виду продукції відома ціна реалізації Цj . Позначимо через Хj невідому величину, яка означає обсяг доцільного виробництва j-го виду продукції. При таких даних математична задача має вид. Необхідно знайти оптимальний обсяг роботи кожного виду, щоб сумарна вартість виготовленої продукції була найбільша:
Ц1Х1 + Ц2Х2 + Ц3Х3 +... + ЦпХп 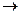 max
max
C11Х1 + C12Х2 + C13Х3 +... + C1nХп 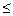 b1
b1
C21Х1 + C22Х2 + C23Х3 +... + C2nХп 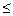 b2
b2
..................................................................
Cm1Х1 + Cm2Х2 + Cm3Х3 +... + CmnХп 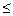 bm
bm
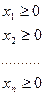
|
х= 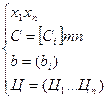
Транспортна задача.
Нехай використовуються тільки транспортний ресурс одного виду продукції.
Нехай існує m пунктів, де зосереджені запаси цієї продукції (пункт відправки постачання).
Нехай існує п споживачів цієї продукції, які розміщені в різних пунктах (пункт призначення споживання).
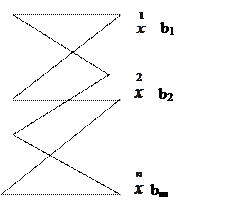
|
Нехай задані величини 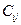 - витрати на одиницю продукції, на перевезення з і-го пункту постачання до j-го пункту призначення. Визначимо змінні
- витрати на одиницю продукції, на перевезення з і-го пункту постачання до j-го пункту призначення. Визначимо змінні 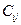 обсяги перевезення продукції із і-го пункту постачання до j-го пункту призначення:
обсяги перевезення продукції із і-го пункту постачання до j-го пункту призначення:
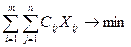

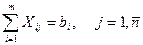

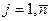
В класичній транспортній задачі критерієм оптимальності може бути час перевезень, пункт перевезень.
Задача про призначення.
Нехай існує на деякому підприємстві m вакантних посад, на які претендує п кандидатів. Допустимо, що ми можемо оцінити ефективність будь-якої посади будь-яким кандидатом. 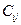 - ефективність використання j-тим кандидатом і-тої посади.
- ефективність використання j-тим кандидатом і-тої посади.
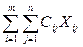

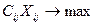
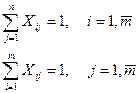
 0 або 1
0 або 1
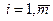
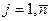
Задача про розміщення виробничих потужностей.
Нехай розглядається m можливих пунктів для розміщення виробництва деякого виду продукції. Нехай аі – максимальна потужність в і-тому пункті. Продукція із можливих пунктів поставлення п- споживачам, для кожного з яких відомапотреба bj. Необхідно знайти пункти виробництва та схеми перевезень. Позначимо Хі - доцільний обсяг виробництва в і-тому пункті, а 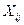 - обсяги перевезень продукції від і-того виробника до j-того споживача.
- обсяги перевезень продукції від і-того виробника до j-того споживача.


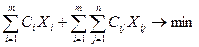 ;
;
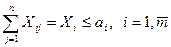 ;
;
 ;
;
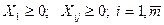 ;
;
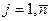 .
.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1055; Нарушение авторских прав?; Мы поможем в написании вашей работы!
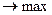 ;
Сх
;
Сх 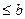 х
х