Решение систем линейных уравнений

MATLAB позволяет работать с объектами линейной алгебры, т. е. векторами и матрицами, настолько просто, насколько это вообще возможно.

Яркий пример этому – решение систем линейных уравнений.

Пример:

Пусть дана система линейных уравнений

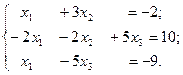
Решить систему с применением оператора обратного деления матриц < \ >.

Решение:

В матричной записи система имеет вид Ах = b, где

A =, b =, х =

– соответственно матрица из коэффициентов при неизвестных, вектор-столбец из свободных членов и вектор-столбец из неизвестных.

Введем матрицу А и вектор-столбец свободных членов b:

>> А=[1 3 0;-2 -2 5;1 0 -5]

А =

1 3 0

-2 -2 5

1 0 -5

>> b=[-2;10;-9]

b =

-2

-9

Известно, что система имеет единственное решение, если определитель матрицы А не равен нулю (│ A │ = det (A) ≠ 0). Вычислим определитель матрицы А:

>> disp(det(A))

-5

Определитель не равен нулю. Находим решение системы с помощью оператора обратного деления матриц < \ >:

>> x=А\b

x =

-1

Проверим полученное решение x₁ = 1, x₂ = -1, x₃ = 2 подстановкой в систему уравнений:

>> disp(A*x)

-2.0000

10.0000

-9.0000

В результате проверки получен вектор-столбец свободных членов. Значит, получено верное решение системы.

Найдем теперь решение системы х = A^-1b с помощью обратной матрицы. Вначале вычислим обратную матрицу A^-1:

>> A1=inv(A)

A1 =

-2.0000 -3.0000 -3.0000

1.0000 1.0000 1.0000

-0.4000 -0.6000 -0.8000

Находим решение системы:

>> A1*b

ans =

1.0000

-1.0000

2.0000

Отметим, что решение системы с помощью обратной матрицы требует больше времени и памяти, к тому же этот способ может дать большую погрешность решения. Поэтому для решения линейных систем рекомендуется применять оператор обратного деления < \ >.

Пример:

Решить систему линейных уравнений

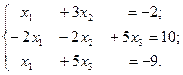
Решение:

>> A=[1 3 0;-2 -2 5;1 0 5]

A =

1 3 0

-2 -2 5

1 0 5

>> b=[-2 10 -9]

b =

-2 10 -9

>> disp(det(A))

Находим решение системы:

>> x=A\b'

x =

-7.5714

1.8571

-0.2857

Заметим, что обратное деление произведено на вектор-столбец b', поскольку вектор b введен как вектор-строка. Получили приближенное решение системы. Вычислим обратную матрицу A^-1:

>> disp(inv(A))

-0.2857 -0.4286 0.4286

0.4286 0.1429 -0.1429

0.0571 0.0857 0.1143

Точное решение системы и точная обратная матрица выражаются через рациональные дроби:

>> format rat

>> x=A\b'

x =

-53/7

13/7

-2/7

>> disp(inv(A))

-2/7 -3/7 3/7

3/7 1/7 -1/7

2/35 3/35 4/35

Дата добавления: 2014-12-07