Твердая кристаллическая среда 2 страница

По П. Д. Данкову, на поверхности подложки происходят два различных кристаллизационных процесса: образование двумерного зародыша под влиянием направляющих сил поверхности подложки и одновременно образование трехмерного зародыша, для которого не обязательна определенная ориентация по отношению к подложке. Эпитаксия связана с образованием двумерного зародыша. Между решетками подложки и кристаллизующегося вещества обычно не существует полного соответствия, следовательно, двумерный зародыш несколько деформируется. Если эта деформация достаточно велика, энергетически более выгодным может оказаться образование трехмерного зародыша, и в этих случаях эпитаксия не наблюдается. Т.о., основное условие эпитаксии записывается в виде:

А₂^D = A₂⁰ + E_D ≤ A₃, (1.34)

где А₂^D - работа образования деформированного двумерного зародыша; A₂⁰- работа образования недеформированного двумерного зародыша тех же размеров; А₃ – работа образования трехмерного зародыша; Е_D – работа деформации. Так как A₂⁰ << A₃,

А₂^D ≥ E_D.

Сейчас в отношении гетерогенного зародышеобразования имеются три основных точки зрения: 1) оно происходит статистически из двумерного газа; 2) оно протекает только на активных центрах, преимущественно на точечных дефектах, и 3) компромиссная точка зрения, согласно которой при малых пересыщениях зародышеобразование происходит избирательно, а при больших – статистически.

Первой точки зрения придерживался Л. С. Палатник, работы которого по изучению механизма конденсации металлического пара в вакууме указывают на возможность образования кристаллической фазы либо непосредственно из пара (по схеме п 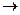к), либо через жидкую фазу (по схеме п 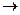ж 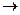к). Начальную стадию образования конденсата на нейтральной подложке можно представлять как «двумерную кристаллизацию» или сжижение «двумерного металлического пара», образующегося на подложке. Механизм конденсации в вакууме определяется температурой подложки и плотностью газового потока.

Работы Г. И. Дистлера дают материал в пользу второй точки зрения, согласно которой кристаллизация представляет собой репликационный процесс, запрограммированный в электрически активной структуре поверхности кристалла – подложки. Подложки действуют в качестве электрически активных матриц. Активная структура кристаллов слагается из различных структурных дефектов, главную роль среди которых играют точечные.

Группа ученых, начиная с И. Странского и Р. Кашиева, П. Данкова и Г. Близнакова придерживается мнения, что принципиально возможно два механизма образования эпитаксиальных пленок: непрерывный рост и спонтанная кристаллизация. В первом случае процесс роста осуществляется за счет присоединения атомов у активных центров подложки: изломов, ступенек, недостроенных атомных плоскостей, дислокаций, скоплений дефектов и т.п. Желательно, чтобы скорость роста слоя вдоль поверхности была больше скорости возникновения нового слоя.

Спонтанное образование зародышей облегчено, когда пересыщение превышает критическое значение, в некоторый момент могут образоваться зародыши приблизительно одинакового размера, и до определенного момента число их будет увеличиваться без существенного изменения размеров. По мере осаждения трехмерные зародыши разрастаются вплоть до образования сплошной пленки. Поскольку маловероятно, чтобы расстояния между кристаллами оказались величинами, в точности кратными периодам их решетки, то при встрече растущих кристаллов образуются дефекты. Часто трудно судить, является ли тонкая пленка в действительности сплошной или нет. Структуру обычно определяют с помощью малоугловой дифракции электронов.

Подложка должна быть монокристальной с гладкой поверхностью. Если на поверхности подложки высота ступеньки велика, то соответственно крупные ступеньки образуются и в пленках. В качестве подложек часто используют поверхности скола каменной соли и слюды. Нередко выгодны металлические подложки, поскольку осажденные на них пленки становятся сплошными при меньших толщинах и содержат меньше дефектов, чем в пленках, выращенных на подложках – ионных кристаллах.

Существенный фактор при эпитаксиальном росте – температура подложки, которая влияет на критический размер и скорость образования, а также на подвижность адсорбированных атомов. Предполагается определенная «температура ориентации», ниже и выше которой ориентация затруднена. При «температуре ориентации» скорость образования зародышей мала, адсорбированные частицы сохраняют такую подвижность на поверхности подложек, которая способствует занятию наиболее благоприятных с энергетической точки зрения положений на подложке. Плена растет из меньшего числа зародышей с небольшим числом дефектов, возникающих при соприкосновении зародышей.

Эпитаксиальная температура зависит как от свойств подложки, так и от скорости осаждения. По мере увеличения скорости осаждения пленки становятся менее совершенными, что связано и с более значительной их разориентировкой.

В общем случае действует правило: структурное совершенство тем выше, чем меньше исходные концентрации веществ и чем выше температура подложек.

Экспериментально показано, что ориентация происходит в две стадии: в стадию роста и коалесценции (слияния островков в одну пленочку). Коалесценция вступает в действие уже при заметных расстояниях между частицами (~ 100 – 1000 Å).

Можно различить эпитаксию I и II рода.

Эпитаксия I рода – текстурированные слои, которые отвечают условию:

(h₁ k₁ l₁) || (h₂ k₂ l₂). Это кристаллизация на подложках с одномерной ориентацией, где единые кристаллы могут быть любым образом повернуты относительно друг друга и соответственно подложка может быть бесструктурной, аморфной.

В эпитаксии I рода предполагается постепенный переход неориентированного первого слоя новой фазы в ориентированные последующие слои.

Эпитаксия II рода – ориентация двух направлений относительно симметрии подложки.

4) Факторы, влияющие на зарождение кристаллов

Из уравнения (1.24) видно, что важнейшим фактором в зарождении кристаллов остается движущая сила кристаллизации; те же факторы, которые способствуют протяженности метастабильной области, так или иначе препятствуют зарождению кристаллов.

На зарождение кристаллов оказывают влияние соприкасающиеся с жидкостью поверхности твердых тел, в частности стенка сосуда. Отдельные участки неоднородной поверхности обладают по отношению к образованию новой фазы различной активностью, которая определяется как физико-химической природой участка, так и его геометрической формой и размерами. Зарождению кристаллов способствуют и такие дефекты на поверхностях твердых тел, как трещины и каналы почти молекулярного размера.

На зарождение центров кристаллизации влияет число «обработок», предшествующих опыту и заключающихся в том, что выращенные из раствора кристаллы растворяются в свежей порции того же растворителя. Из полученного раствора вновь выращиваются кристаллы, которые тут же подвергаются растворению и т.д. С другой стороны, с ускорением перемешивания выравнивается концентрация и температура системы и снижается вероятность флуктуационного образования зародышей. При увеличении числа чередующихся операций скорость зарождения кристаллов падает. Обработку нужно рассматривать как способ самоочистки вещества от нагреваемых примесей, часть которых всегда оттесняется поверхностью растущего кристалла.

Перемешивание ускоряет возникновение зародышей, при этом его влияние носит сложный характер. Скорость диффузионного подвода кристаллизующего вещества к образующемуся зародышу увеличивается одновременно с дополнительным отщеплением твердых частиц с поверхностей, контактирующих с раствором.

Перемешивание и другие внешние воздействия (направленный теплоотвод, воздействие ультразвуковых, электрических и других полей) создают также флуктуации плотности и энергии и тем самым способствуют появлению жизнеспособных зародышей.

При воздействии электрических и магнитных полей число возникающих центров кристаллизации находятся в прямой зависимости от напряженности поля. В этих полях молекулы вещества (переохлажденной жидкости), ориентируясь в одном направлении, создают анизотропную среду, во многом аналогичную кристаллической. Воздействие магнитного поля уменьшает дефектность структуры быстро выращиваемых кристаллов из водных растворов.

Незначительные высокочастотные колебания воздействуют на кристаллизацию. Ультразвуковое поле настолько ускоряет процесс кристаллизации, что в результате получаются слитки с дендритной структурой. Механизм действия ультразвука в ультразвуковом поле сводится к происходящему на границе раздела двух фаз отщеплению мельчайших кристаллов, совершающих колебательные движения и увеличивающихся в размерах. Такое «почкование» способствует лавинообразному разрастанию процесса зарождения. Срастаясь с кристаллом, зародыши образуют поликристаллический слиток. Скорость этого процесса зависит от интенсивности ультразвукового поля.

Велика роль ионизирующего излучения, например γ-излучения радия. Его эффект сводится к увеличению числа центров кристаллизации. За счет поляризующего действия возникающих ионов на нейтральные молекулы первые становятся центрами окружения как ионов противоположного знака, так и этих молекул, и вокруг образующейся достаточно устойчивой группы начинается рост кристаллов.

Тема 2: Теории роста кристаллов.

В настоящее время наиболее развиты теории послойного роста кристаллов (молекулярно-кинетические и дислокационная) и теории нормального, или молекулярно-шероховатого, роста кристаллов из расплавов, и признан кристаллохимический подход в объяснении процессов кристаллизации.

Лекция 1. Механизмы роста кристаллов.

1) Механизм роста кристаллов двумерными зародышами.

Согласно теории Косселя кристалл растет посредством повторимого хода, путем встраивания частиц в структуру только в при­вилегированных местах роста, которыми служат изломы (положе­ния у полукристалла). Повторимые ходы частиц, увеличивая объем кристалла, не изменяют его поверхности, следовательно, не изменяют и поверхностной энергии.

С другой стороны, источниками из­ломов на плотноупакованной гладкой (сингулярной) грани служат ступени. Последние благодаря высокой плотности изломов пред­ставляют собой своего рода стоки для адсорбированных одиноч­ных атомов. В условиях роста ступенчатые участки (на вицинальных гранях) выклиниваются, оставляя позади себя сингулярную поверхность, дальнейший рост которой возможен при появлении новых источников ступеней.

Этими источниками ступеней служат двумерные зародыши, дислокации, места соприкосновения между кристаллом и его кон­тейнером, границы зерен между двумя соприкасающимися крис­таллами различной ориентации, инородные макроскопические частицы, двойники и т. д.

Энергии ступеней разной генерации и частоты присоединения в них (ступенях) неодинаковы, поэтому выделяют механизм роста сингулярной грани двумерными зародышами и дислокационный механизм.

Несингулярная грань растет нормальным механизмом. Механизм нормального роста определяется непрерыв­ным присоединением частиц по всей шероховатой поверхности, равномерно покрытой изломами, количество которых не лимитиру­ет скорости кристаллизации.

При больших в метастабильной области рост кристалла может идти за счет присоединения уже имеющихся в среде трех­мерных агрегатов частиц («зародышей», «ассоциатов»). С увеличением движущей силы кристаллизации доля, вносимая в скорость роста этим механизмом, должна увеличиваться.

Покажем, что кинетика кристаллизации бездефектной сингу­лярной грани при небольших отклонениях системы от равновесия лимитируется скоростью образования двумерного зародыша I_n. Согласно расчетам (Бартон и др., 1959) вероятность (скорость) образования двумерного зародыша мала вплоть до относительного пересыщения β в несколько десятков процентов. Тангенциальное же разрастание его Λ происходит с большой ско­ростью.

Скорость движения одиночной прямолинейной ступени «элементарной» (соответствующей в кристалле Косселя ребру элементарной ячейки) высоты. Ступени, расту­щие на поверхности кристалла, имеют фронт, изрезанный излома­ми. Адсорбированные на грани частицы образуют адсорбционный слой, находящийся в равновесии с изломами и окружающей крис­талл средой. Если равновесие нарушается, то в местах изломов, переход частиц в твердую фазу ведет к возникновению на поверх­ности плоских потоков. Расход вещества в адсорбционном слое пополняется за счет поступления новых молекул из окружающей среды. Таким образом, непосредственно конденсация происходит на боковых участках ступеней. Процесс роста ступени из газовой фазы определяется движением частиц по схеме: пар 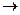адсорбционный слой 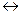ступень, вдоль ступени 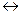излом.

Вероятность прямого попадания атома из пара вступень или ее излом мала, так как площадь торца ступени составляет всего лишь ~ 0,01% от площади вицинальной грани. Плотность же из­ломов велика, диффузия атомов вдоль ступени к излому не может быть лимитирующей стадией. Равновесие адсорбцион­ный слой - ступень достигается мгновенно.

Общий поток атомов j_V за счет объемной диффузии из пара в адсорбционный слой равен:

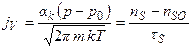(2.1)

где α_к - коэффициент конденсации (аккомодации) для перехода пар 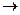адсорбционный слой, меньший единицы; коэффициент а_к представляет собой отношение числа частиц, «застрявших» в ад­сорбционном слое к числу частиц, столкнувшихся с ним, так как часть их отражается поверхностью этого слоя. Пренебрегая дви­жением ступени и учитывая большую скорость обмена адатомов с изломами, можно j_V выразить через концентрацию адатомов в адсорбционном слое, достигшего стационарного состояния: ,

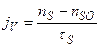где 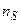- действительная концентрация адатомов на поверхности вдали от ступени при условии равновесия с газовой фазой; 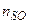-равновесная поверхностная концентрация адатомов, равная кон­центрации у ступени; τ_S - время жизни адатома на поверхности до ухода его в пар. Величина 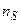определяется 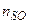и сте­пенью пересыщения γ:

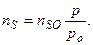(2.2)

Диффузионный закон Фика (для одномерного диффузионного потока вдоль оси у, перпендикулярной к ступени) записывается в виде:

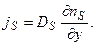(2.3)

Наименьшая длина стока (у) частиц, прилипших к плоской по­верхности, к ступени определяется длиной их свободного пробега X_S. Заменяя в формуле (2.3) 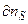потоком на ступень (n_S - n_SO), y - X_S получим выражение скорости движения пря­молинейной ступени Λ_∞:

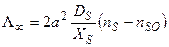, (2.4)

здесь множитель 2 определяется потоком частиц к ступени с двух сторон, а ² — площадь, занимаемая одной частицей, 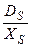- скорость поверхностной диффузии.

Для того чтобы выразить Λ_∞ через пересыщение, вспомним, что 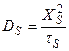(из уравнения Эйнштейна), а также 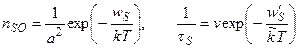, (2.2) и подставим их в формулу (2.4). Тогда

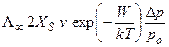(2.5)

где W - полная энергия испарения адатома, равная .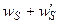

Физический смысл уравнения (2.5) состоит в следующем. Молекулы, ударившись о поверхность кристалла в «диффузион­ной зоне» шириной в 2X_S, будут адсорбироваться на движущейся ступени с большим числом мест обмена (изломов). Скорость, с которой движется край слоя, пропорциональна относительному пересыщению 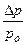. По достижении слоем края кристалла его «творческая» функция прекращается, он образует завершенную поверхность. Дальнейший рост возможен только при образовании новой ступени. Сравнение двух скоростей I_n и Λ говорит в пользу второй, находящейся не в экспоненциальной зависимости от 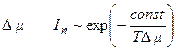, а в линейной Λ ~ Δμ. Медленная стадия роста сингулярной грани, стадия образования на ней дву­мерного зародыша (ступени) и будет лимитирующей.

И. Н. Странский и Р. Каишев (1939) указывают на следующую зависимость нормальной скорости роста грани V(λ) от переохлаж­дения ΔТ:

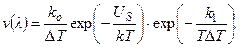(2.6)

где k₀ - множитель, слабо зависящий от температуры; U_s - энергия активации, требуемая для присоединения новых атомных рядов к периферии двумерного зародыша; k₁ — константа, свя­занная с существованием энергетического порога для образова­ния двумерного зародыша на грани растущего кристалла. В этой формуле предполагается, что каждый образующийся зародыш разрастается на всю плоскость. Если одновременно образуется несколько зародышей на грани, то скорость роста грани будет меньше. Такие и более сложные ситуации будут рассмотрены позднее.

График зависимости скорости роста v(λ) от пересыщения (рис. 2.1) подтвержден экспериментально на примере роста крис­талла из пара. Можно видеть, что существует некоторое крити­ческое пересыщение β_k, необходимое для образования двумерных зародышей. При β > β_k скорость роста сингулярной грани не лими­тируется скоростью образования двумерных зародышей и линей­но зависит от пересыщения. В растворах подобные зависимости однозначно определить трудно из-за адсорбированной «шубы» из растворителя. Признаком двумерного зародышеобразования мо­жет служить образование слоев у ребер и вершин. Однако такое образование часто происходит благодаря особенностям диффузи­онного поля около кристалла.

Р. Каишевым (1966) достаточно убедительно доказано дву­мерное зарождение и распространение слоев при электрокристал­лизации на совершенных гранях кри­сталлов серебра. При подаче тока на торец кристалла Ag, растущего из раст­вора азотнокислого серебра в форме капилляра, автор добивался получения прерывистого прохождения тока в виде отдельных импульсов. Эта прерывис­тость определяется прерывистым харак­тером кристаллизации серебра, во время которой и проходил ток. Количество электричества, протекающего за один им­пульс, соответствует числу электронов, необходимых для восстановления того ко­личества серебра, которое перекрывает площадь капилляра моноатомным слоем.

Кривая на рис. 2.1 отражает идеали­зированную зависимость v = f(ΔT). В ре­альных системах свой вклад в рост кри­сталла могут вносить двумерные зароды­ши при малых пересыщениях благодаря наличию примесей в среде или ступеней иного происхождения, в связи с чем можно наблюдать смещение кривой v(λ) - β влево.

В работах А. Н. Колмогорова и др. указывается, что зависи­мость нормальной скорости роста грани от пересыщения, в свою очередь, существенно влияет на размеры этой грани. К моменту появления нового зародыша на данном участке поверхности предыдущий разрастается до размера ~ 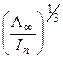, где Λ_∞ ~ Δμ. Если размер грани кристалла 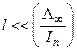то ее нормальная скорость:

v(λ) ~ I_nl². (2.7)

При обратном неравенстве нормальная скорость:

v(λ) ~ а(Λ²_∞ I_n)^{1 / 3} (2.8)

и не зависит от размера грани.

Существенно, что вокруг каждой ступени создается область пониженного пересыщения (n_SO), где образование зародышей маловероятно.

Если передвигается эшелон параллельных ступеней (рис. 2.2), расстояние между которыми ∆r, то скорость движения одиночной ступени выразится:

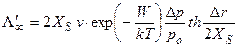, (2.9)

где 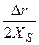- величина отклонения поглощающей поверхности от вертикали. При Δr >> X_S (угол θ мал) 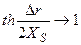, и уравнение (2.8) сводится к (2.5). При Δr << X_S (угол θ велик) 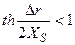и соответственно 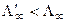,т. е. скорость движения ступеней должна снижаться с уменьшением Δr.

А. А. Чернов (1961) дает более точное выражение зависимости скорости движения ступени от Δr, с учетом времени релаксации τ, необходимого для восстановления равновесия вблизи ступени; времени жизни молекулы в состоянии адсорбции на поверхности τ _S; величины отклонения поглощающей поверхности от вертикали 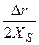; кинетического коэффициента кристаллизации ступени β_СТ, характеризующего скорость обмена частицами между ступенью и адсорбционным слоем:

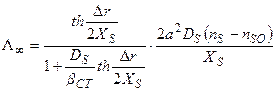, (2.10)

где 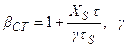– степень пересыщения.

График зависимости 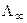от Δr представлен на рис. 2.3. Кривая 1соответствует малому значению β_СТ по сравнению с величинойскорости поверхностной диффузии 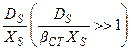. Это имеет место, если кристаллизация затруднена, например, химической реакцией. Кривая 2отвечает обратному соотношению двух скоростей .

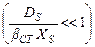Нормальная скорость роста грани связана со ско­ростью движения ступени зависимостью:

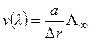, (2.11)

где 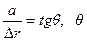- угол отклонения вицинального холмика от ориентации плотноупакованной грани.

Из вышеизложенного следует вывод: с уменьшением Δr (в об­ласти Δr < X _S) увеличивается θ, сокращается величина Х₀, увеличивается плотность изломов. Предельный случай (2.11), когда Δr = а, грань приобретает округлую форму, становится атомно-шероховатой и растет не послойным, а нормальным механизмом, при кото­ром

.

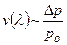Исходя из соотношений (2.1), (2.2), (2.4), (2.10) и (2.11) полу­чаем уравнение для нормальной скорости роста кристалла из паров:

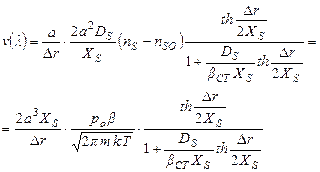(2.12)

где 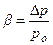- относительное пересыщение (не смешивать с β_СТ - кинетическим коэффициентом кристаллизации ступени).

Графическое изображение зависимости и v(λ) от 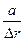дано на рис. 2.4.

2) Дислокационный механизм роста.

В классической теории роста скорость перемещения идеально гладкой (плотноупакованной) грани растущего кристалла пропорциональна частоте появления на ней двумерных (плоских) зародышей (новых атомарных или молекулярных слоев). Разрастание слоя, или перемещение краев неукомплектованных зародышей, происходит достаточно быстро и можно думать, что оно не лимитирует скорости кристаллизации. Вероятность образования нового слоя ничтожна при пересыщениях ниже 25 – 50%. Однако реальные кристаллы растут с наблюдаемыми скоростями при пересыщении 1% или ниже, и большинство правильных и хорошо образованных кристаллов получается в действительности при низких пересыщениях. Все это указывает на то, что реальные кристаллы несовершенны.

Одно из несовершенств кристаллов – дислокации, обеспечивающие наличие готовых ступеней на поверхности плотноупакованной грани кристалла.

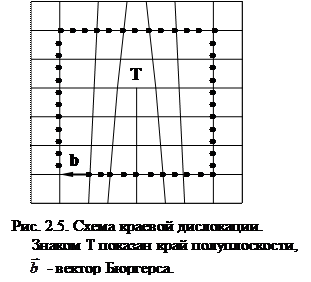На любой плоскости идеальной решетки кристалла можно провести линию через ближайшие соседние атомы так, что она образует замкнутую плоскую петлю. Такая линия называется контуром Бюргерса. Подобная линия в реальном кристалле, имеющем геометрический дефект дислокационного типа, не образует замкнутой петли. Дислокация – это линейное несовершенство, для которого контур Бюргерса разомкнут; вектор, замыкающий разомкнутый контур, называется вектором Бюргерса (рис. 2.5 и 2.6).

Различают краевые, винтовые, косые или криволинейные дислокации.

Краевую дислокацию удобно представить себе так, что в разрез кристаллической решетки вставлена добавочная полуплоскость (рис. 2.5). Край полуплоскости образует линию – ось дислокации, которая простирается вдоль всего кристалла. В краевой дислокации вектор Бюргерса перпендикулярен оси дислокации. Если вектор 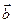параллелен оси дислокации ВВ′, определяют винтовую дислокацию (рис. 2.6). Краевые и винтовые дислокации – крайние разновидности дислокаций. Косые, или криволинейные, дислокации представляют собой промежуточные по ориентировке 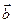относительно оси дислокации.

Может быть вставлено несколько полуплоскостей, тогда вектор Бюргерса соответственно увеличивается. Дислокации различаются по знаку, в зависимости от того, «сверху» (+) или «снизу» (-) вставлена полуплоскость в случае краевой дислокации. В положительной винтовой дислокации движение вдоль контура Бюргерса от более высокого уровня к низкому происходит по часовой стрелке (см. рис. 2.6), в отрицательной – против часовой стрелки.

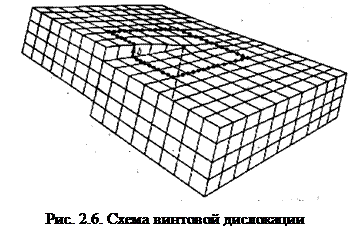Положительная и отрицательная винтовые дислокации дают начало спиралям роста, закручивающимся соответственно по часовой стрелке и против неё. Атомные плоскости в кристалле расположены вокруг оси дислокации по спирали по правому или левому винту. На расстояниях, превышающих несколько межмолекулярных расстояний от линии дислокации, искажение кристалла сглаживается.

Исходной позицией дислокационной теории роста является наличие в кристалле винтовых дислокаций. Дислокация характеризуется избыточной энергией, которая суммируется из энергии оборванных или искаженных связей в ядре дислокации и энергии слабых напряжений вокруг дислокаций (упругих напряжений). Энергия дислокации зависит от механических свойств кристалла и прямо пропорциональна квадрату вектора Бюргерса, который вдоль дислокации остается неизменным, поэтому дислокация не может кончаться в кристалле.

Дата добавления: 2014-12-07