Арифметические операции и арифметические выражения

Понятие операции, выражения и операнда.

Арифметические операции и выражения

Правила умолчания о типах данных и их изменение.

В Фортране допускается не объявлять объекты данных (переменные, именованные константы и функции) целого и вещественного типов. В таких случаях тип данных объекта устанавливается автоматически в соответствии со следующими правилами умолчания: объекты данных, имена которых начинаются с букв i, j, k, l, m, n (или, разумеется, I, J, K, L, M, N), считаются объектами данных целого типа (integer), а все остальные объекты имеют вещественный тип (rEAL). Например:

integer(4):: n=10! n - целая переменная y=2*n; m=2*n! y – переменная типа REAL, m - типа INTEGER

Заметим, что сформулированные выше правила умолчания не распространяются на часть встроенных функций.

С каждым типом данных связан набор встроенных операций.

Выражение − это формула, по которой вычисляется значение. Выражение состоит из операндов и нуля или более операций. Используемые в выражениях операции разделяются на двухместные и одноместные (+, -). В двуместной операции участвуют два операнда, в одноместной (унарной) − один.

Операндами выражения являются объекты данных или их подобъекты. Выражение может присутствовать в правой части оператора присваивания, операторах ввода, вызовах процедур и др. Общий вид выражения, в котором присутствуют двуместные операции:

операнд операция операнд операция...

Заметим, что в Фортране унарным операциям не может предшествовать знак другой операции.

Значение каждого операнда должно быть определено, а результат должен иметь математический смысл (так, например, не должно быть деления на ноль).

В зависимости от типов операндов выражения подразделяются на арифметические, логические, символьные и производного типа. Для выражений первых трех типов в Фортране определены встроенные операции. В выражениях производного типа операции должны быть заданы программистом (для производных типов данных не определено ни одной встроенной операции). Операции различаются старшинством или приоритетом.

Для числовых типов данных используются арифметические операции:

** − возведение в степень;

*, / − умножение и деление;

+, - − одноместные (унарные) плюс и минус;

+, - − сложение и вычитание.

Заметим, что указанные операции перечислены в порядке убывания приоритета их исполнения. В частности, как видно, операция возведения в степень является операцией с наивысшим приоритетом, а операции сложения и вычитания имеют низший приоритет.

Арифметическое выражение состоит из числовых операндов и арифметических операций. Если в выражении присутствует несколько операций, они, кроме возведения степень, выполняются в соответствии с приоритетом слева направо. Операции возведения в степень выполняются справа налево. Для изменения порядка выполнения операций используются круглые скобки. Так, например, записи -x-y+z и (((-x)-y)+z) эквивалентны. Тоже можно сказать и в отношении записей x**y**z и (x**(y**z)). В свою очередь, очевидно, что результаты выполнения операторов присваивания

k1=2**8/2+2; k2=2**(8/2+2); k2=2**(8/(2+2))

будут различными. А именно, переменные k1, k2 и k3 получат в результате значения 130, 64 и 4 соответственно. В общем случае результатом арифмети-

ческого выражения может быть целое, вещественное или комплексное число.

Арифметические операции в Фортране имеют свои особенности, на которых следует остановиться подробнее, перечислив их ниже.

1. На результате арифметических операций сказывается то, что все числа хранятся в памяти компьютера с конечным числом значащих цифр. Таким образом, арифметические выражения с вещественными и комплексными операндами зачастую вычисляются неточно (при сложении, вычитании и умножении пропадают младшие разряды результата; деление, как правило, не может быть выполнено точно, например, 1./3.=0.333333...). Следует иметь в виду, что во всех случаях в Фортране происходит не округление, а отбрасывание (усечение) младших разрядов результата, не умещающихся в ячейке памяти. В силу указанной специфики, в частности, нельзя сравнивать вещественные числа на предмет точного равенства или неравенства, а необходимо выполнять их сравнение с некоторой точностью

2. Операция возведения в степень производится по-разному в зависимости от показателя степени. Если показатель – целая переменная, целая константа или арифметическое выражение целого типа, то возведение в степень производится путем последовательного умножения:

a**3 ® a*a*a; b**(–2) ® 1./ (b*b).

Если же показатель имеет вещественный тип, то для выполнения возведения в степень транслятор использует формулу

.

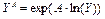Следовательно, возведение в степень с вещественным показателем определено только при . Например, нельзя вычислить выражение y**(1./3) при y = –8, хотя вообще-то . По той же причине при x = 0 нельзя вычислить x**2., но можно вычислить x**2 или x*x.

Таким образом, операция возведения в степень имеет ограничения (ограниченную область действия). В частности, запрещается возводить отрицательное число в нецелочисленную степень. Кроме того, нельзя возводить ноль в отрицательную или нулевую степень.

3. Запрещается делить на ноль (что согласуется с традиционными математическими правилами).

4. Результат арифметических операций с целыми числами всегда есть целое число. Это существенно при делении целых чисел и при возведении целого числа в отрицательную степень (в остальных случаях результат и так целый). Следует отметить, что в Фортране при делении целых чисел и возведении целого числа в целую отрицательную степень, дробная часть результата отбрасывается (без учета знака). Поясним сказанное на примере, рассматривая следующую программу:

real(4) x, y, z, w! описание используемых переменных x=7/4; y=-7/4! присваивание значений z=2**(-2); w=(-1)**(-3)! переменным x, y, z и w print *,’x=’,x,’ y=’,y,’ z=’,z,’ w=’,w! Вывод результатов на экран end! Обязательный последний оператор программы

В результате выполнения данной программы переменным x и y будут присвоены значения 1 и -1 соответственно, вместо, казалось бы, естественных в таком случае 1.75 и -1.75. Иными словами результатом деления двух целых чисел в Фортране является целая часть получаемого частного. После проведения целочисленного деления, в связи с тем, что переменные x и y имеют тип REAL(4), целые числа 1 и -1 будут преобразованы в стандартный вещественный тип.

Для того, чтобы получить в приведенной выше программе ожидаемые (естественные) с точки зрения обычной арифметики ответы следует записать:

x=7./4. или x=7./4 или x=7/4. и y=-7./4. или y=-7./4 или y=-7/4.

вместо второй и третьей строки программы соответственно.

Что касается переменных z и w, также используемых в программе, то они получают значения 0 и -1 соответственно (результаты возведения целых чисел в целые степени – целые числа).

5. В арифметических выражениях не следует комбинировать переменные, отличающиеся на несколько порядков, например:

real(4):: x=1.E+30, y=-1.E+30, z=7. print *,(x+y)+z! 7.000000 (правильно) print *,x+(y+z)! 0.000000E+00 (неправильно)

6. В Фортране допускается (хотя и не рекомендуется) использование в арифметическом выражении разных типов и разных разновидностей типов. Каждый тип арифметического операнда характеризуется определенным рангом. Перечислим эти типы ниже в порядке убывания рангов

complex(8) или DOUBLE COMPLEX – наивысший ранг;

complex(4)

real(8)

real(4)

INTEGER(4) или INTEGER

INTEGER(2)

INTEGER(1) или byte

Результат каждой операции выражения определяется в соответствии со следующими правилами:

· если операнды арифметической операции имеют один и тот же тип, то и результат операции имеет тот же тип (важнейший пример – операция целочисленного деления);

· если операнды операции имеют различный тип, то результат имеет тип операнда наивысшего ранга.

Поясним оба правила на примере.

integer(2):: x=1, y=2 real(4):: z=2.5 real(8) w1, w2 w1=x/y*z! 0.0_8 w2=x/(y*z)! 0.2_8

При вычислении w2 первоначально выполняется операция умножения, но прежде число 2 типа INTEGER(2) переводится в тип real(4). Далее выполняется операция деления, и вновь ее предваряет преобразование типов: число 1 типа INTEGER(2) переводится в тип real(4). Выражение возвращает число 0.2 типа real(4), которое после в результате присваивания преобразовывается в тип real(8). В ходе выполнения указанных действий типы операндов x и y, разумеется, сохраняются.

Результат вычисления w1 является очевидным следствием целочисленного деления и действий отчасти аналогичных описанным выше. Заметим, что для исключения целочисленного деления в выражениях вещественного типа с целочисленными операндами можно пользоваться явными преобразованиями типов данных, например (ниже это float):

integer(2):: x=2, y=4 real(4):: z=4, q1, q2 q1=z**(x/y)! 1.000000 q2=z**(float(x)/float(y))! 2.000000

7. Переходы к большей или меньшей разновидности типа могут сопровождаться потерей точности, например:

real(4):: x=1.11 real(8):: y y=x print*,x! 1.110000 print*,y! 1.110000014305115

Но, если сразу начать работу с типом real(8), то точность сохраняется:

real(4):: x, y x=1.11_8; y=1.11d0 print*,x! 1.110000000000000 print*,y! 1.110000000000000

Как уже отмечалось, переход к низшей разновидности типа также может сопровождаться искажением значения, например:

integer(2):: x=325 integer(1):: y! -128 <= y <= 127 y=x print*,x! 325 print*,y! 69

8. Следует следить за тем, чтобы результат выражения не превышал допустимых для данной разновидности значений. Так, например, имеем:

integer(1):: a=100, b=100, c integer(2):: d! -128 <= y <= 127 c=a+b! Ошибка – неверно! d=a+b! Верно print*,c,d! -56 200

Дата добавления: 2014-12-07