
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аппроксимация и устойчивость разностной схемы. Рассмотрим задачу Дирихле для уравнения
|
|
|
|
Разностная схема
Постановка задачи
Рассмотрим задачу Дирихле для уравнения

 y
y
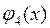

 1
1
 D
D 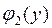
 0
0  1 x
1 x
с краевыми условиями


Будем считать, что правая часть дифференциального уравнения 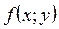 и функции
и функции  ,
, 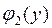 ,
,  ,
, 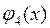 удовлетворяет условиям, обеспечивающим существование и единственность гладкого решения
удовлетворяет условиям, обеспечивающим существование и единственность гладкого решения  задачи (1) - (2).
задачи (1) - (2).
Построим разностную схему - разностный аналог дифференциальной задачи (1) - (2).
Выполним следующие шаги:
1) Область непрерывного изменения аргументов  заменим дискретным множеством точек – сеткой
заменим дискретным множеством точек – сеткой  ,
, 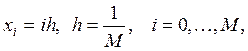
 Точки
Точки 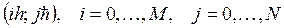 называются узлами сетки
называются узлами сетки  ,
,  и
и 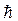
 называются шагами сетки по оси
называются шагами сетки по оси 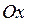 и
и  , соответственно. Узел
, соответственно. Узел  сетки
сетки  будем обозначать
будем обозначать  . Обозначим множество внутренних узлов сетки через
. Обозначим множество внутренних узлов сетки через  и через
и через  - множество граничных узлов.
- множество граничных узлов.
Сетку 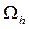 можно представить в виде
можно представить в виде

где  ,
,  .
.
Замечание. При реализации метода сеток шагиобычно выбирают согласованно. Поэтому сетка и обозначена через  .
.
2) Все функции в исходной дифференциальной задаче (1) – (2) заменим сеточными функциями - функциями, определенными в узлах сетки  . Сеточную функцию обозначим через
. Сеточную функцию обозначим через 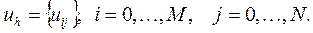 Проекцию функции
Проекцию функции  на сетку
на сетку  обозначим через
обозначим через 
3) Производные в исходной дифференциальной задаче (1) – (2) заменим разностными отношениями – сходящимися формулами численного дифференцирования:

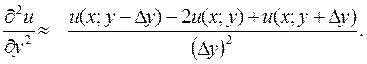
В результате получим систему линейных алгебраических уравнений:
 (3)
(3)
Система (3) называется разностной схемой - разностным (дискретным) аналогом дифференциальной задачи (1) – (2).
Для построения разностной схемы (3) используется пять точек – пяти-точечный шаблон:
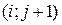
 |

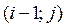



Введем пространства сеточных функций  и
и 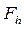 .
.

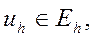
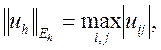


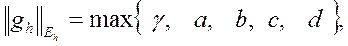
где 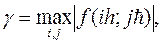
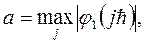



Теперь разностную схему (3) можно записать в виде операторного уравнения


где 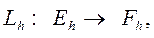
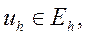

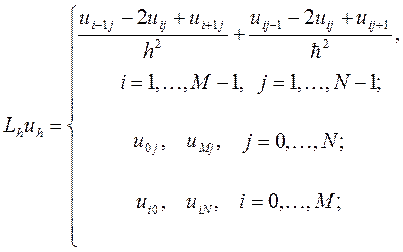
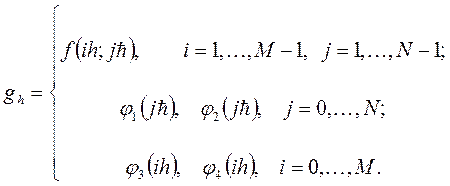
Разностная схема (4) аппроксимирует исходную дифференциальную задачу (1) - (2) на ее решении  если
если
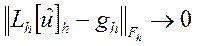 при
при 
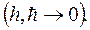 .
.
Разность  называется невязкой.
называется невязкой.
Покажем, что невязка 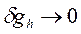 при
при  .
.
Так как
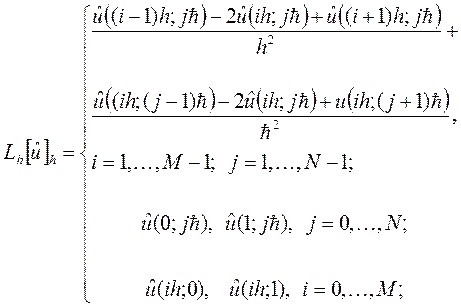
то, заменяя здесь 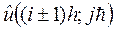 и
и 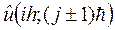 соответствующими разложениями решения
соответствующими разложениями решения  по формуле Тейлора в точке
по формуле Тейлора в точке 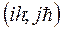 :
:

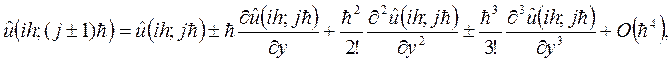 получаем
получаем
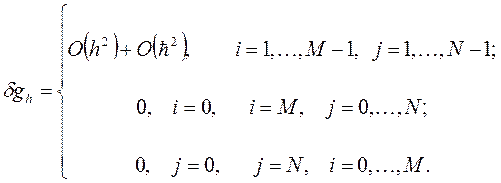
Следовательно, 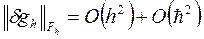 и разностная схема (4) обладает свойством аппроксимации.
и разностная схема (4) обладает свойством аппроксимации.
Разностная схема (4) называется устойчивой, если для достаточно малых шагов сетки  и
и  выполнены условия:
выполнены условия:
1) Для любой сеточной функции  уравнение
уравнение  имеет единственное решение
имеет единственное решение 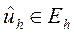 (существует обратный оператор
(существует обратный оператор 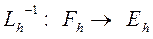 ).
).
2) Существует константа  , независящая от
, независящая от  (
( и
и  ), такая, что для решения
), такая, что для решения 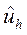 уравнения
уравнения  имеет место неравенство
имеет место неравенство

(норма обратного оператора равномерно по  ограничена константой
ограничена константой  :
:  ).
).
Замечание. Условие 2) определения устойчивости разностной схемы принято называть условием устойчивости.
Проверку устойчивости разностной схемы (4) разобьем на несколько этапов.
Предложение 1. Пусть сеточная функция 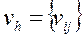 определена на всей сетке
определена на всей сетке  и отлична от константы (не все координаты вектора
и отлична от константы (не все координаты вектора 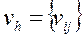 равны одному и тому же числу). Пусть на множестве внутренних узлов сетки
равны одному и тому же числу). Пусть на множестве внутренних узлов сетки 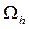 имеет место неравенство
имеет место неравенство
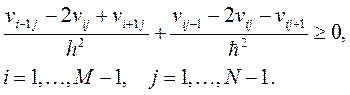
Тогда сеточная функция 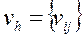 принимает свое наибольшее значение в одном из граничных узлов сетки
принимает свое наибольшее значение в одном из граничных узлов сетки

Предложение 2. Пусть сеточная функция  определена на всей сетке
определена на всей сетке  и отлична от константы. Пусть на множестве внутренних узлов сетки
и отлична от константы. Пусть на множестве внутренних узлов сетки 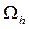 имеет место неравенство
имеет место неравенство

Тогда сеточная функция  принимает свое наименьшее значение в одном из граничных узлов сетки
принимает свое наименьшее значение в одном из граничных узлов сетки
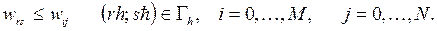
Из Предложений 1 и 2 немедленно следует
Предложение 3. Если существуетсеточная функция 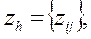 определенная на всей сетке
определенная на всей сетке  , такая, что на множестве внутренних узлов сетки
, такая, что на множестве внутренних узлов сетки 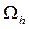 имеет место равенство
имеет место равенство

то она достигает своего наибольшего и наименьшего значений на множестве граничных узлов 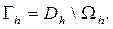
Отсюда немедленно получаем выполнение условия 1) определения устойчивости разностной схемы. Действительно из предложения 3 следует, что однородная разностная схема 
 для всех
для всех  имеет только нулевое решение
имеет только нулевое решение  для всех
для всех  Таким образом, неоднородное уравнение
Таким образом, неоднородное уравнение  имеет единственное решение
имеет единственное решение 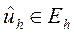 для любой сеточной функции
для любой сеточной функции 
Перейдем к доказательству условия устойчивости.
Заметим, что для любого многочлена второй степени
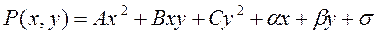
имеет место равенство

Положим
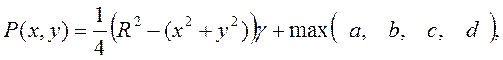
где 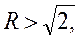
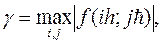
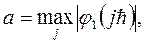



Введем оператор  :
:
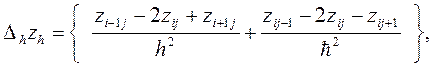

Имеем



Рассмотрим разность 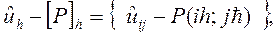 где
где 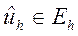 - решение разностной схемы.
- решение разностной схемы.
Очевидно, что

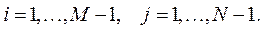
Так как  для
для  то из Предложения 1 следует, что сеточная функция
то из Предложения 1 следует, что сеточная функция 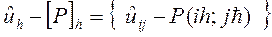
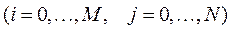 достигает своего наибольшего значения в одном из граничных узлов и, следовательно,
достигает своего наибольшего значения в одном из граничных узлов и, следовательно, 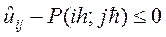 или
или  во всех узлах сетки
во всех узлах сетки  .
.
Теперь рассмотрим сеточную функцию  . Применив к этой функции оператор
. Применив к этой функции оператор  , получим
, получим
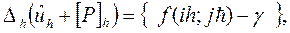
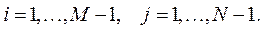
Так как 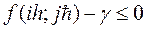 для
для  то из Предложения 2 следует, что сеточная функция
то из Предложения 2 следует, что сеточная функция 
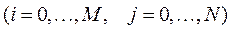 достигает своего наименьшего значения в одном из граничных узлов и, следовательно,
достигает своего наименьшего значения в одном из граничных узлов и, следовательно,  или
или  во всех узлах сетки
во всех узлах сетки  .
.
Таким образом,
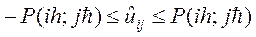
во всех узлах сетки  . Следовательно,
. Следовательно,

и условие устойчивости для разностной схемы (4) выполняется с константой  .
.
По теореме Филиппова из аппроксимации и устойчивости разностной схемы получаем ее сходимость:
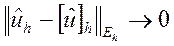 при
при 
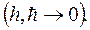 ,
,
здесь 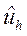 - решение разностной схемы (3) (или что тоже самое (4)),
- решение разностной схемы (3) (или что тоже самое (4)),  - точное решение исходной дифференциальной задачи (1) – (2).
- точное решение исходной дифференциальной задачи (1) – (2).
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1125; Нарушение авторских прав?; Мы поможем в написании вашей работы!