Постановка и решение задач Линейного Программирования

Лекция № 3

Четвергая группа — интерпретационные методы

Третья группа — методы обработки полученных результатов

Третью группу (по Б. Г. Ананьеву) составляют методы обработки полученных результатов. Это ограниченное единство количественного и качественного, содержательного анализа. Обработка результатов — это всегда творческий, поисковый процесс, предполагающий подбор наиболее адекватных и чувствительных математических средств.

Наконец, четвертую группу составляют так называемые интерпретационные методы, направленные на теоретическое объяснение, психологическую трактовку изучаемого явления. Здесь всегда присутствует комплексный, системный набор различных вариантов функционального и структурного методов, замыкающих общий цикл психологического исследования.

Наблюдения (более пассивны)	Эксперименты (более активны)
Научный метод исследования не ограниченный простой регистрацией фактов, а научно-объясняющие причины того или иного психологического явления	Активное вмешательство исследователя в деятельность испытуемого с целью создания условий, в которых выявляется психологический факт
Житейские наблюдения ограничиваются регистрацией фактов, носят случайный неорганизованный характер	Научный метод наблюдения переходит от написания фактов к объяснению его внутренней сущности. Необходимое условие четкий план, фиксация результатов в спец. дневнике	Лабораторный протекает в специальных условиях. Используется спец. аппаратура	Естественный протекает в обычных условиях. Применяется при изучении познавательных возможностей на разных возрастных этапах
Вспомогательные методы психологии
Анализ продуктов деятельности и биографический метод	Близнецовый метод, социометрия, моделирование, анкеты, тесты

3.1. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ

Экономико-математическая задача (ЭМЗ) включает четыре группы элементов.

1. Неизвестные задачи. Их обозначим через x_j где j — номер переменной. Номер переменной (j = 1,..., n) изменяется от 1 до n или .

2. Известные величины правых частей уравнений и неравенств или свободные члены. Их насчитывается столько же, сколько имеется ограничений. Обозначим свободные члены через А_i, В_i и т. д., где i — номер ограничения. Номер ограничения
(i = 1,..., m) изменяется от 1 до m ().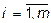

3. Известные величины при переменных, или технико-экономические коэффициенты а_ij. Коэффициенты а_ij обозначаются в зависимости от того, в какой строке (i) и при какой переменной (j) они находятся. В этом состоит двойственность данных коэффициентов. Например, а _12,24 обозначает коэффициент 12-й строки, стоящей при 24-й переменной.

4. Коэффициенты F-строки или целевой функции 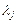. Этих коэффициентов насчитывается столько же, сколько имеется переменных.

В совокупности свободные члены А_i, В_i, технико-экономические коэффициенты а_ij, коэффициенты F -строки 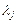составляют исходную информацию ЭМЗ. Содержание переменных, а также значения исходной информации зависят от объекта или процесса, по информации которых задача составляется.

Механизм взаимосвязи элементов позволяет сформировать
общую (типичную) ЭМЗ. Например, найти x_j, т. е. значения переменных j при условиях:

а ₁₁ x ₁ + а ₁₂ x ₂ + а ₁₃ x ₃, +... + а _{1 n}x_n В ₁;

а ₂₁ x ₁ + а ₂₂ x ₂ + а ₂₃ x ₃, +... + а _{2 n}x_n ≥ В ₂;

а ₃₁ x ₁ + а ₃₂ x ₂ + а ₃₃ x ₃, +... + а _{3 n}x_n = В ₃;

а ₄₁ x ₁ + а ₄₂ x ₂ + а ₄₃ x ₃, +... + а _{4 n}x_n ≤ В ₄;

………………………………

а_{m 1} x ₁ + а_{m 2} x ₂ + а_{m 3} x ₃, +... + а_mnx_n ≤ В_m;

x_j ≥ 0, j = ;

F_max =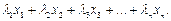

Таким образом, имеется ЭМЗ, состоящая из m строк (или ограничений) и n столбцов (или переменных), т. е. из системы ограничений. В задаче присутствуют все четыре группы элементов. Взаимосвязи элементов в конкретных условиях будут определять содержание и типы ограничений, а также характер взаимосвязи элементов исходной информации. Типы ограничений в задаче обычно бывают следующими: меньше — равно (≤), больше — равно (≥) и равно (=).

Решение экономико-математической задачи связано с нахождением значений переменных x_j, которые будучи подставленными в ограничения задачи, обеспечивают выполнение требований этих ограничений: уравнений или неравенств, а функции F придают экстремальное (т. е. минимальное либо максимальное) значение.

Одно из требований ограничений состоит в том, что если задача решается на максимум, то среди системы уравнений и неравенств должно быть хотя бы одно ограничение типа меньше — равно либо равно (при решении на минимум — хотя бы одно ограничение типа больше — равно либо равно). Следует отметить, что при отсут-
ствии названных ограничений величины переменных практически ничем не ограничены и решение задачи теряет смысл

Другие требования к содержанию задачи вытекают из теории математического программирования, основные положения которой, имеющие непосредственное отношение к составлению экономико-математических задач, изложены ниже.

Таким образом, решение ЭМЗ предполагает такой вариант решения системы неравенств и уравнений, при котором функция F принимает максимальное значение (при решении задачи на максимум) или минимальное (при решении задачи на минимум). Отсюда следует, что содержание экономико-математической задачи, с одной стороны, должно включить в себя множество альтернативных вариантов, с другой стороны, — позволять выбрать такой вариант, при котором значение функции отвечало бы конкретным требованиям производства.

Для решения системы неравенств и уравнений ЭМЗ необходимо, чтобы содержание и взаимосвязи ее элементов соответствовали требованиям теории определителей, матриц, векторных пространств и выпуклых множеств.

3.2 Формирование минимальной продовольственной корзины

Эту задачу часто называют задачей о рационе. Пусть определен ассортимент продуктов и известны их характеристики (цена; калорийность; содержание белков, жиров, углеводов, витаминов). Требуется найти набор минимальной стоимости, обеспечивающий формирование минимальной продовольственной корзины.

Введем обозначения:

n – число рассматриваемых продуктов;

m – количество учитываемых веществ (в т. ч. калорий);

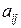– содержание i -го вещества в j -м продукте, (); ;

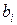– потребность человека в i -м веществе, ;

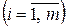– стоимость единицы j -го продукта,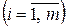

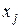– количество j -го продукта в решении, .

Получим модель, симметричную по отношению к ранее записанной. Только вместо максимума теперь нужно найти минимум, изменились и знаки ограничений

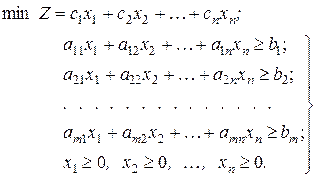
Разумеется, и в этом случае может потребоваться введение определенных соотношений между отдельными группами продуктов, ограничение содержания некоторых ингредиентов и т. д.

Дата добавления: 2014-12-07