
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Властивості та графіки тригонометричних функцій
|
|
|
|
Формули перетворення добутку тригонометричних функцій у суму
Основні формули тригонометрії
Виділяють такі основні групи тригонометричних формул:
1. Основні співвідношення між тригонометричними функціями того самого аргументу (див. §4).
2. Формули додавання аргументів:
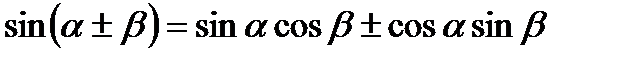 ;
;
 ;
;
 ;
;
 .
.
3. Формули подвійного і потрійного аргументів:
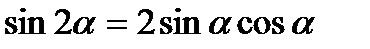 ;
;
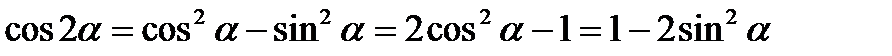 ;
;
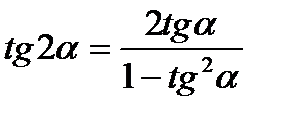 ;
;
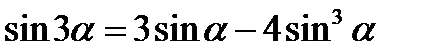 ;
;
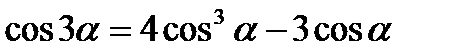 ;
;
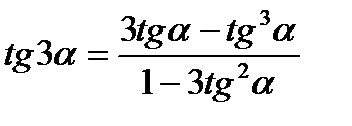 .
.
4. Формули зниження степеня:
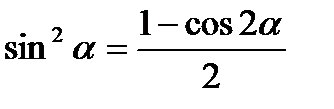 ;
; 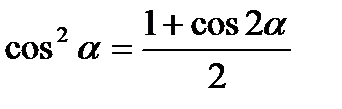 .
.
 ;
; 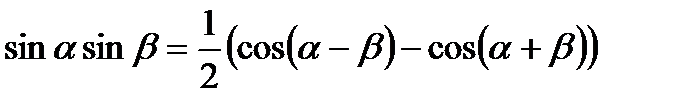 ;
;
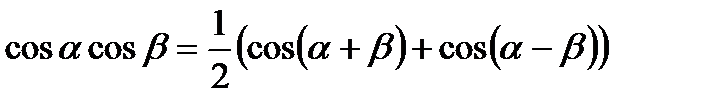 .
.
6. Формули перетворення суми і різниці однойменних тригонометричних функцій у добуток:
 ;
;
 ;
;  ;
;
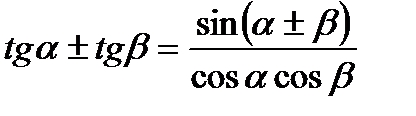 ;
; 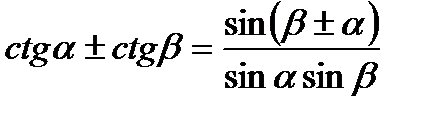 .
.
7. Формули тригонометричних функцій половинного аргументу:
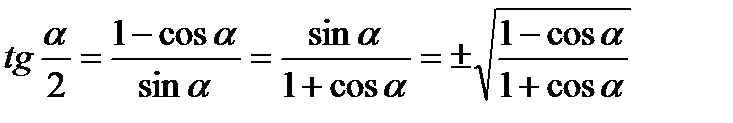 ;
; 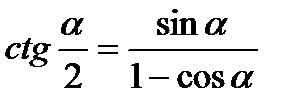 ;
;
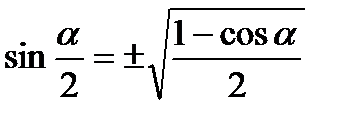 ;
; 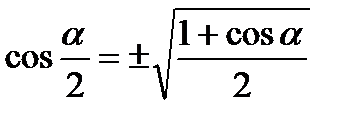 .
.
33. Спростіть вирази:
1) 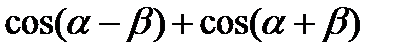 ; 2)
; 2) 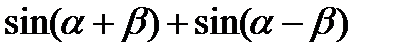 ;
;
3) 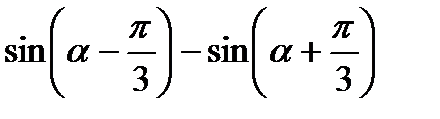 ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 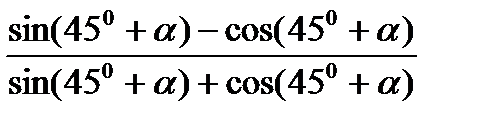 ;
;
9) 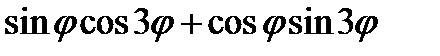 ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13) 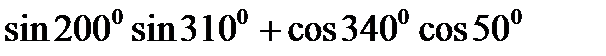 ; 14)
; 14) 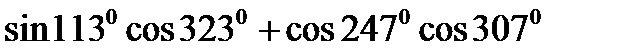 ;
;
15) 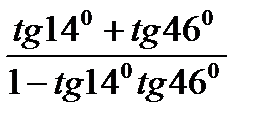 ; 16)
; 16) 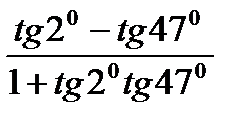 ;
;
17) 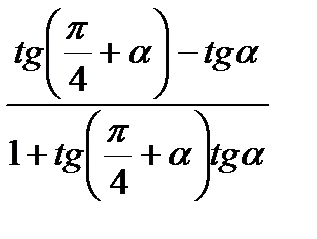 ; 18)
; 18) 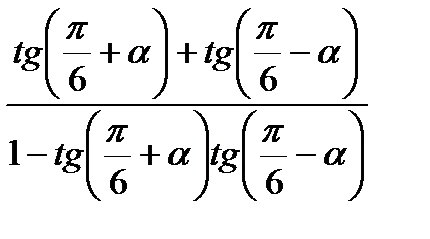 .
.
34. Доведіть тотожність:
1)  ; 2)
; 2) 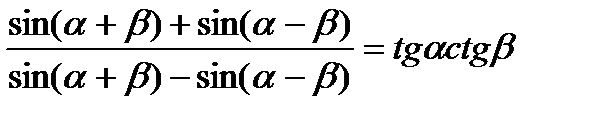 ;
;
3)  ; 4)
; 4) 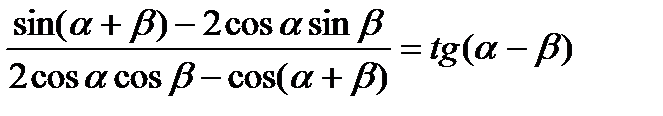 ;
;
5) 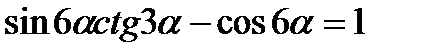 ; 6)
; 6) 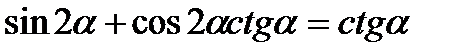 ;
;
7) 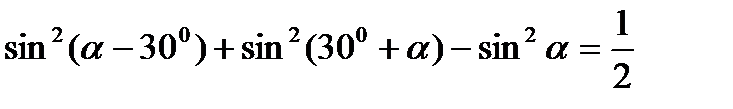 ; 8)
; 8)  ;
;
9) 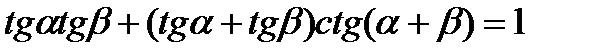 ; 10)
; 10) 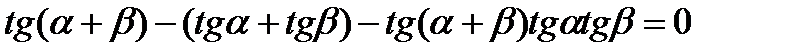 .
.
35. Знайдіть:
1) 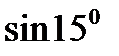 ; 2)
; 2) 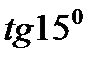 ;
;
2) 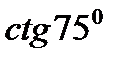 ; 4)
; 4) 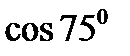 ;
;
3) 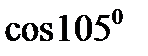 ; 6)
; 6) 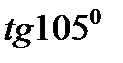 .
.
36. 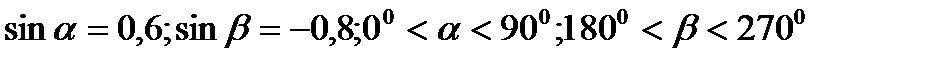 . Знайдіть
. Знайдіть  .
.
37. 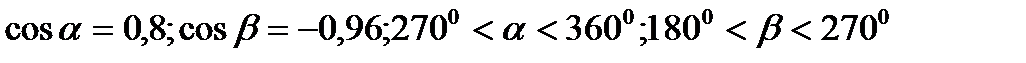 . Знайдіть
. Знайдіть  .
.
38. Знайдіть значення виразу:
1) 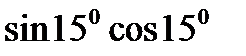 ; 2)
; 2) 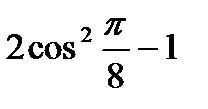 ;
;
3) 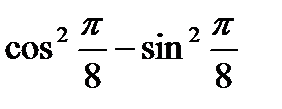 ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 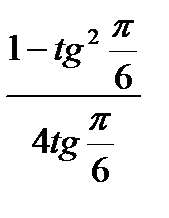 .
.
39. Спростіть вирази:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5) 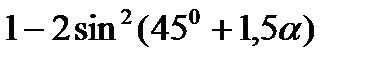 ; 6)
; 6) 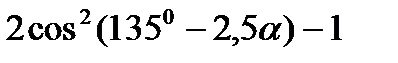 ;
;
7) 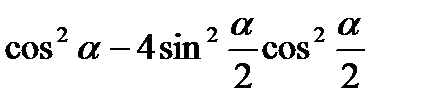 ; 8)
; 8) 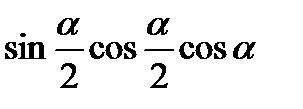 ;
;
9) 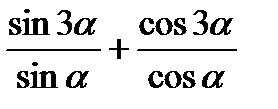 ; 10)
; 10) 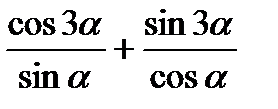 ;
;
11) 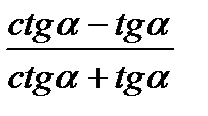 ; 12)
; 12) 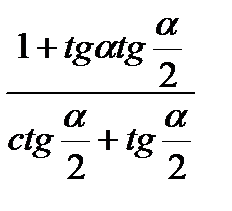 ;
;
13) 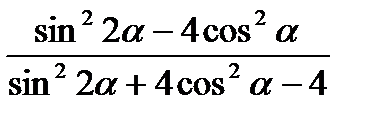 ; 14)
; 14) 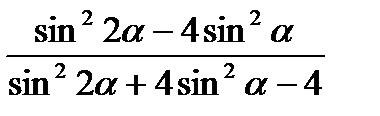 ;
;
15) 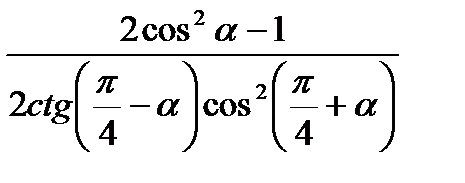 ; 16)
; 16)  .
.
40. Перетворіть на добуток:
1) 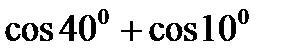 ; 2)
; 2) 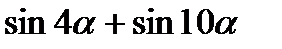 ; 3)
; 3) 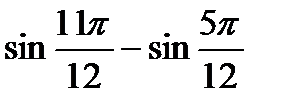 ; 4)
; 4) 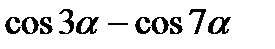 ;
;
5)  ; 6)
; 6)  ;
;
7) 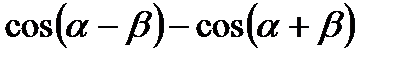 ; 8)
; 8) 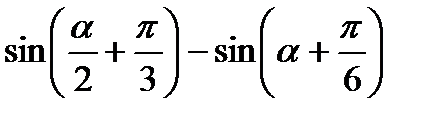 ;
;
9)  ; 10)
; 10) 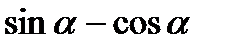 ;
;
11)  ; 12)
; 12) 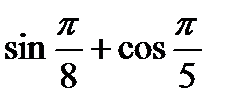 ;
;
13) 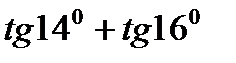 ; 14)
; 14)  ;
;
15) 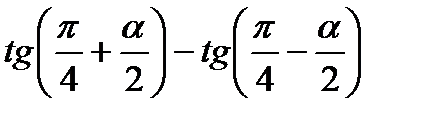 ; 16)
; 16) 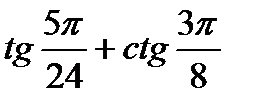 ;
;
17)  ; 18)
; 18) 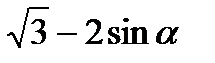 ;
;
19) 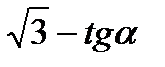 ; 20)
; 20)  .
.
41. Доведіть тотожність:
1) 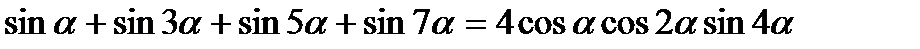 ;
;
2) 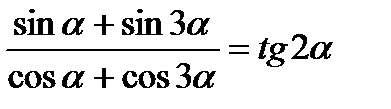 ;
;
3) 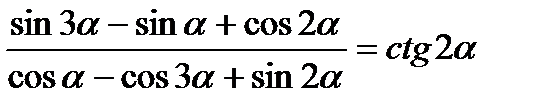 ;
;
4) 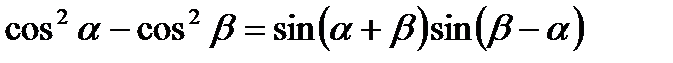 .
.
до змісту
Властивості та графік функції 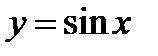
1. Область визначення – уся числова пряма, тобто 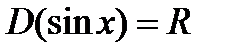 ;
;
2. Область значень – відрізок  , тобто
, тобто 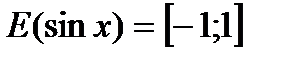 ;
;
3. Функція 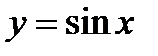 – непарна, тобто
– непарна, тобто 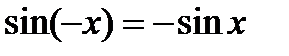 ; графік симетричний відносно початку координат;
; графік симетричний відносно початку координат;
4. Функція періодична з основним періодом 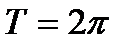 ;
;
5. Нулі функції: 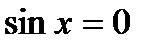 при
при 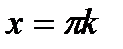 ,
,  ;
;
6. Інтервали знакосталості:
А) 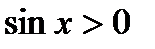 , якщо
, якщо 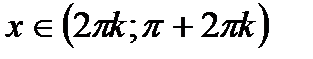 ,
,  ;
;
Б) 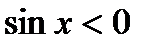 , якщо
, якщо 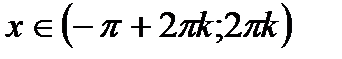 ,
,  ;
;
7. Інтервали зростання й спадання:
А) Функція 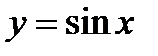 зростає на проміжках
зростає на проміжках 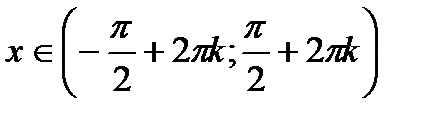 ,
,  ;
;
Б) Функція 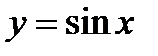 спадає на проміжках
спадає на проміжках 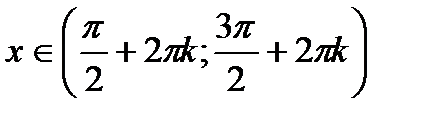 ,
,  ;
;
8. Екстремуми функції:
А) 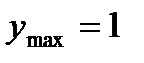 при
при 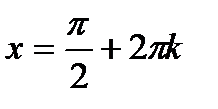 ,
,  ;
;
Б)  при
при 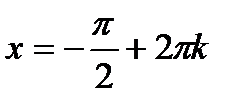 ,
,  ;
;
9. Функція 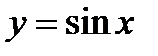 є обмеженою,
є обмеженою, 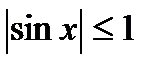 .
.
Графік функції 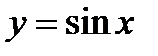 називається синусоїдою, він показаний на рис. 2.
називається синусоїдою, він показаний на рис. 2.
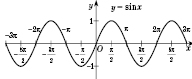 Рис. 2
Рис. 2
Властивості та графік функції 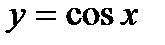
1. Область визначення – уся числова пряма, тобто  ;
;
2. Область значень – відрізок  , тобто
, тобто  ;
;
3. Функція 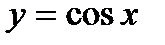 – парна, тобто
– парна, тобто 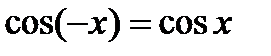 ; графік симетричний щодо осі Оу;
; графік симетричний щодо осі Оу;
4. Функція періодична з основним періодом 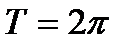 ;
;
5. Нулі функції:  при
при  ,
,  ;
;
6. Інтервали знакосталості:
А) 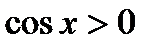 , якщо
, якщо 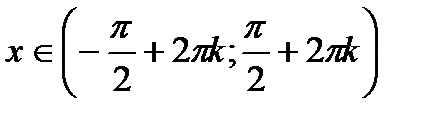 ,
,  ;
;
Б) 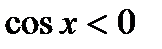 , якщо
, якщо 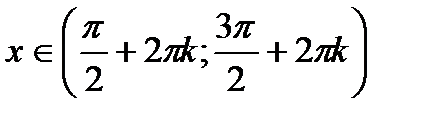 ,
,  ;
;
7. Інтервали зростання і спадання:
А) Функція 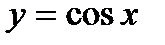 зростає на проміжках
зростає на проміжках 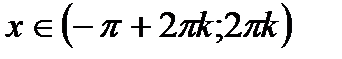 ,
,  ;
;
Б) Функція 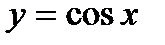 спадає на проміжках
спадає на проміжках 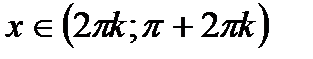 ,
,  ;
;
8. Екстремуми функції:
А) 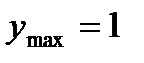 при
при 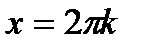 ,
,  ;Б)
;Б)  при
при 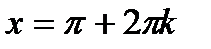 ,
,  ;
;
9. Функція 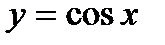 є обмеженою,
є обмеженою, 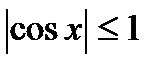 .
.
Графік функції 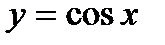 називається косинусоїдою, він показаний на рис. 3.
називається косинусоїдою, він показаний на рис. 3.
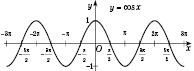 Рис. 3
Рис. 3
Властивості та графік функції 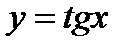
1. Область визначення – множина усіх дійсних чисел, крім чисел виду  ,
,  , тобто
, тобто  ,
,  ;
;
2. Область значення – вся числова пряма, тобто 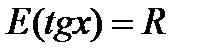 ;
;
3. Функція 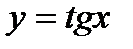 – непарна, тобто
– непарна, тобто 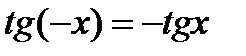 , графік симетричний відносно початку координат;
, графік симетричний відносно початку координат;
4. Функція періодична з основним періодом 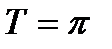 ;
;
5. Нулі функції 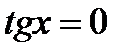 при
при 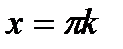 ,
,  ;
;
6. Інтервали знакосталості:
А) 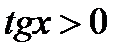 , якщо
, якщо  ,
,  ;
;
Б) 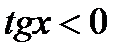 , якщо
, якщо 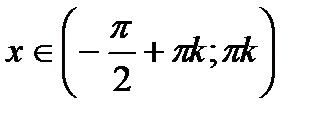 ,
,  ;
;
7. Інтервали зростання і спадання: функція 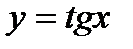 зростає на проміжках
зростає на проміжках 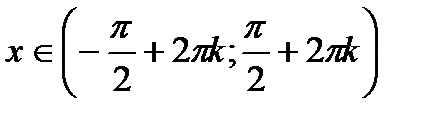 ,
,  ;
;
8. Функція 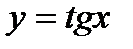 екстремумів не має;
екстремумів не має;
9. Функція 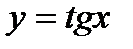 не обмежена.
не обмежена.
Графік функції 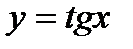 називається тангенсоїдою, він показаний на рис. 4.
називається тангенсоїдою, він показаний на рис. 4.
Прямі 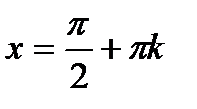 ,
,  називаються вертикальними асимптотами графіка функції
називаються вертикальними асимптотами графіка функції 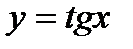
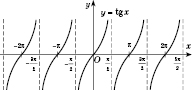 Рис. 4
Рис. 4
Властивості та графік функції 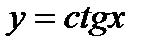
1. Область визначення – множина усіх дійсних чисел, крім чисел виду 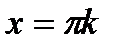 ,
,  , тобто
, тобто  ,
,  ;
;
2. Область значень – вся числова пряма, тобто 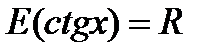 ;
;
3. Функція 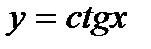 – непарна, тобто
– непарна, тобто  , графік симетричний відносно початку координат;
, графік симетричний відносно початку координат;
4. Функція періодична з основним періодом 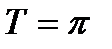 ;
;
5. Нулі функції:  при
при 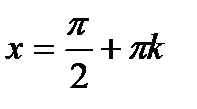 ,
,  ;
;
6. Інтервали знакосталості:
А) 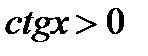 , якщо
, якщо 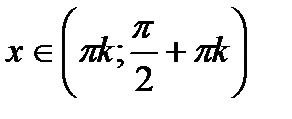 ,
,  ;
;
Б) 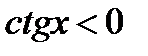 , якщо
, якщо 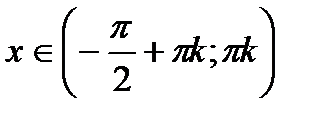 ,
,  ;
;
7. Інтервали зростання і спадання: функція 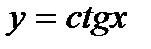 спадає на проміжках
спадає на проміжках 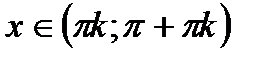 ,
,  ;
;
8. Функція 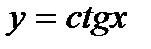 екстремумів не має;
екстремумів не має;
9. Функція 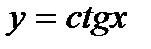 необмежена.
необмежена.
Графік функції 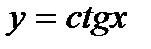 називається котангенсоїдою, він показаний на рис. 5. Прямі
називається котангенсоїдою, він показаний на рис. 5. Прямі 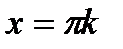 ,
,  називаються вертикальними асимптотами графіка функції
називаються вертикальними асимптотами графіка функції 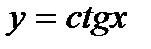 .
.
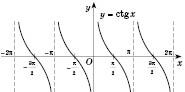 Рис. 5
Рис. 5
42. Побудуйте графіки функцій:
1) 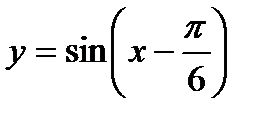 ; 2)
; 2) 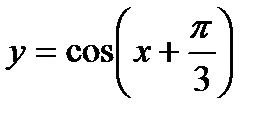 ;
;
3)  ; 4)
; 4) 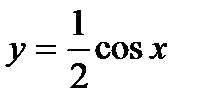 ;
;
5) 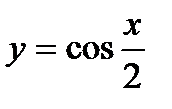 ; 6)
; 6)  ;
;
7) 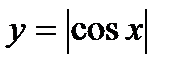 ; 8)
; 8) 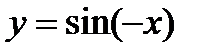 ;
;
9) 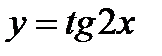 ; 10)
; 10) 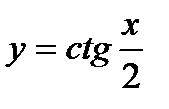 ;
;
11)  ; 12)
; 12) 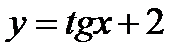 .
.
43. Використовуючи властивості функцій 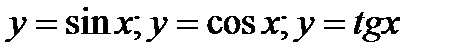 порівняйте числа:
порівняйте числа:
1)  і
і  ; 2)
; 2) 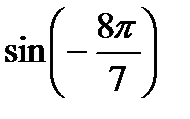 і
і 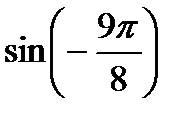 ;
;
3)  і
і 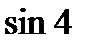 ; 4)
; 4) 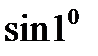 і
і 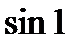 ;
;
5) 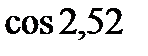 і
і 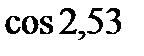 ; 6)
; 6) 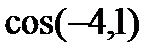 і
і 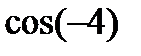 ;
;
7)  і
і 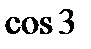 ; 8)
; 8) 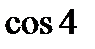 і
і 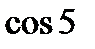 ;
;
9) 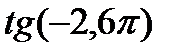 і
і 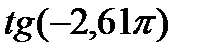 ; 10)
; 10) 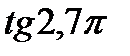 і
і 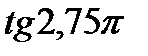 ;
;
11) 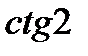 і
і 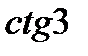 ; 12)
; 12) 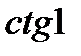 і
і  .
.
44. Розташуйте числа у порядку зростання:
1) 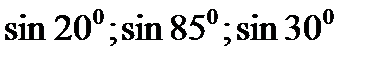 ; 2)
; 2) 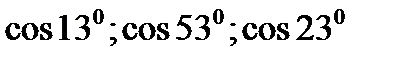 ;
;
3) 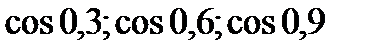 ; 4)
; 4) 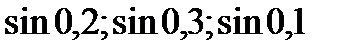 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 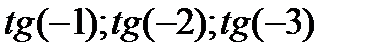 ;
;
45. Побудуйте графік функції 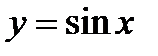 на проміжку
на проміжку  та знайти:
та знайти:
1) значення  , якщо
, якщо 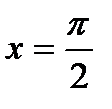 ;
;
2) значення 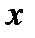 , якщо
, якщо  ;
;
3) проміжок, де функція спадає.
46. Побудуйте графік функції  на проміжку
на проміжку 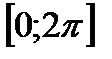 та знайти:
та знайти:
1) значення 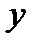 , якщо
, якщо 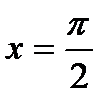 ;
;
2) значення  , якщо
, якщо 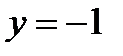 ;
;
3) проміжок, на якому функція зростає.
47. Побудуйте графік функції 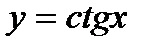 на проміжку
на проміжку 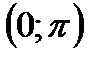 та знайти:
та знайти:
1) значення 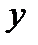 , якщо
, якщо 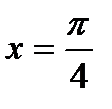 ;
;
2) значення 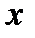 , якщо
, якщо 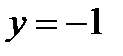 ;
;
3) проміжок, на якому функція спадає.
48. Побудуйте графік функції  на проміжку
на проміжку 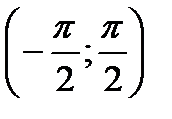 та знайти:
та знайти:
1) значення 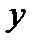 , якщо
, якщо  ;
;
2) значення 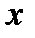 , якщо
, якщо 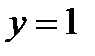 ;
;
3) проміжок, на якому функція зростає.
49. Побудуйте графіки функцій:
1) 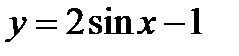 ; 2)
; 2) 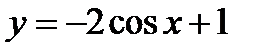 ;
;
3) 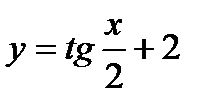 ; 4)
; 4) 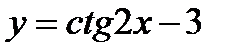 ;
;
5) 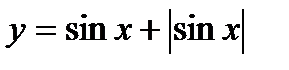 ; 6)
; 6) 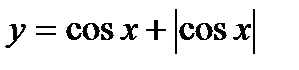 ;
;
7) 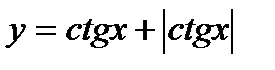 ; 8)
; 8)  .
.
до змісту
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 808; Нарушение авторских прав?; Мы поможем в написании вашей работы!