
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорія ймовірностей – математична наука, яка вивчає закономірності масових випадкових подій
Основні поняття теорії ймовірностей
Масовими називаються події, для яких відповідні випробування можна відтворити необмежену кількість разів, або є можливість спостерігати аналогічні випробування у великій кількості.
До первісних понять теорії ймовірностей належать поняття випробування і поняття події.
У середовищі, яке нас оточує можна спостерігати події (явища), які обов’язково відбудуться, якщо буде виконана визначена сукупність умов. Такі події називають вірогідними.
Події, які ніколи не відбудуться, якщо буде виконана визначена сукупність умов, називаються неможливими.
Події, які при виконанні визначених умов, можуть відбутися, а можуть не відбутися називаються випадковими.
Сукупність умов при виконанні яких подія може відбутися, або не відбутися називається випробуванням, або дослідом.
Повною групою подій називається множина подій таких, що в результаті кожного випробування обов’язково повинна відбутися хоча б одна з них.
Попарно несумісні події – це події, дві з яких не можуть відбутися разом.
Рівноможливі події – це такі події, кожна з яких не має ніяких переваг у появі частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов.
Якщо події:
1) утворюють повну групу подій;
2) є несумісними;
3) є рівноможливими;
То такі події утворюють простір елементарних подій.
Імовірністю випадкової події називається відношення кількості елементарних подій, які сприяють цій події, до кількості всіх рівно можливих несумісних подій, які утворюють повну групу під час певного випробування.
Імовірність позначають  ,
,
де 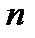 - загальна кількість рівно можливих і несумісних подій, які утворюють повну групу;
- загальна кількість рівно можливих і несумісних подій, які утворюють повну групу;  - число елементарних подій, які сприяють події А.
- число елементарних подій, які сприяють події А.
244. Проаналізуйте приклади випробувань та відповідних їм подій, що подано у таблиці
| Випробування | Випадкова подія |
| Підкидання грального кубика | Поява чотирьох очок на верхній грані |
| Гра в шахи | Виграш у суперника |
| Випуск ламп електроламповим заводом | Поява бракованої лампи |
245. Проаналізуйте дані таблиці і виділіть у ній вірогідні, неможливі та випадкові події.
| № | Випробування | Випадкова подія |
| Нагрівання дроту | Довжина дроту збільшилася | |
| Підкидання гральної кості | Випало два очки | |
| Огляд поштової скриньки | Виявлено три листи | |
| Створення низької температури | Вода перетворилася на лід | |
| Виконання пострілу | Влучено в ціль | |
| Охолоджування тіла | Його об’єм збільшився |
246. Відокремте події і випробування та запишіть результату таблицю:
А) тягнемо екзаменаційний білет, випадає білет № 3;
Б) дістаємо лампу з коробки, вона бракована;
В) набираємо навмання телефонний номер і чуємо голос знайомого;
Г) відкриваємо поштову скриньку і знаходимо лист;
Д) стріляємо і влучаємо в ціль.
| Випробування | Подія | |
| А | ||
| Б | ||
| В | ||
| Г | ||
| Д |
247. З’ясуйте, які із подій є вірогідними:
А – «два попадання при трьох пострілах»;
В– «навмання вибране трицифрове число не більше 1000»;
С – «випадання 12 очок при киданні двох гральних кубиків»;
D – «випадання цифри 3 при киданні монети»?
248. З’ясуйте, які із подій є неможливими:
А – «випадання 13 очок при киданні двох гральних кубиків»;
В – «поява слова «мама» при випадковому наборі букв а, а, м, м»;
С – «чотири попадання при трьох пострілах»;
D – «поява на одній грані грального кубика числа 8»?
249. Вкажіть вірогідні, випадкові і неможливі події, яку можуть відбутися при випробуваннях, записаних у таблиці
| № | Випробування | Випадкова подія | Вірогідна подія | Неможлива подія |
| 1. | Підкидання грального кубика | |||
| 2. | Підкидання монети | |||
| 3. | Витягування кулі зі скриньки, де є чорні та білі кулі | |||
| 4. | Витягування двох гральних карт | |||
| 5. | Два постріли по мішені |
250. З’ясуйте, чи утворюють повну групу такі групи подій:
А) Випробування – кидання монети; події:
 - «поява герба»;
- «поява герба»;
 - «поява цифри».
- «поява цифри».
Б) Випробування – кидання двох монет; події:
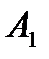 - «поява двох гербів»;
- «поява двох гербів»;
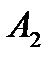 - «поява двох цифр».
- «поява двох цифр».
В) Випробування – два постріли по мішені; події:
 - «жодного попадання»;
- «жодного попадання»;
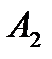 - «одне попадання»;
- «одне попадання»;
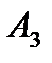 - «два попадання».
- «два попадання».
Г) випробування – два постріли по мішені; події:
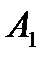 - «хоча б одне попадання»;
- «хоча б одне попадання»;
 - «хоча б один промах».
- «хоча б один промах».
Д) Випробування – витягування карти із колоди карт; події:
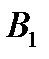 - «поява карти червової масті»;
- «поява карти червової масті»;
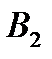 - «поява карти бубнової масті»;
- «поява карти бубнової масті»;
 - «поява карти трефової масті»;
- «поява карти трефової масті»;
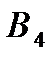 - «поява карти пікової масті»;
- «поява карти пікової масті»;
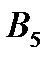 - «поява короля»;
- «поява короля»;
 - «поява дами».
- «поява дами».
251. З’ясуйте, чи є несумісними такі події:
А) Випробування – кидання монети; події:
 - «поява герба»;
- «поява герба»;
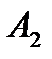 - «поява цифри».
- «поява цифри».
Б) Випробування – два постріли по мішені; події:
 - «жодного попадання»;
- «жодного попадання»;
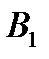 - «одне попадання»;
- «одне попадання»;
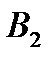 - «два попадання».
- «два попадання».
В) Випробування – кидання двох монет; події:
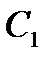 - «поява герба на першій монеті»;
- «поява герба на першій монеті»;
 - «поява цифри на другій монеті».
- «поява цифри на другій монеті».
Г) Випробування – два постріли по мішені; події:
 - «хоча б одне попадання»;
- «хоча б одне попадання»;
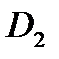 - «хоча б один промах».
- «хоча б один промах».
Д) Випробування – витягування двох карт з колоди; події:
 - «поява двох чорних карт»;
- «поява двох чорних карт»;
 - «поява туза»;
- «поява туза»;
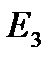 - «поява дами».
- «поява дами».
252. З’ясуйте, чи є рівноможливими такі події:
А) Випробування – кидання монети; події:
 - «поява герба»;
- «поява герба»;
 - «поява цифри».
- «поява цифри».
Б) Випробування – кидання неправильної (зігнутої) монети; події:
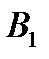 - «поява герба»;
- «поява герба»;
 - «поява цифри».
- «поява цифри».
В) Випробування – постріл по мішені; події:
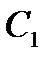 - «влучення»;
- «влучення»;
 - «промах».
- «промах».
Г) Випробування – кидання двох монет; події:
 - «поява двох гербів»;
- «поява двох гербів»;
 - «поява двох цифр»;
- «поява двох цифр»;
 - «поява одного герба і однієї цифри».
- «поява одного герба і однієї цифри».
Д) Випробування – витягування однієї карти із колоди; події:
 - «поява карти червової масті»;
- «поява карти червової масті»;
 - «поява карти бубнової масті»;
- «поява карти бубнової масті»;
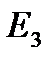 - «поява карти трефової масті»;
- «поява карти трефової масті»;
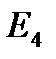 - «поява карти пікової масті».
- «поява карти пікової масті».
Є) Випробування – кидання грального кубика; події:
 - «поява не менше трьох очок»;
- «поява не менше трьох очок»;
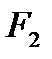 - «поява не більше чотирьох очок».
- «поява не більше чотирьох очок».
253. З’ясуйте, чи утворюють простір елементарних подій такі події:
А) Випробування – кидання монети; події:
 - «поява герба»;
- «поява герба»;
 - «поява цифри».
- «поява цифри».
Б) Випробування – кидання двох монет; події:
 - «поява двох гербів»;
- «поява двох гербів»;
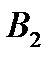 - «поява двох цифр».
- «поява двох цифр».
В) Випробування – кидання грального кубика; події:
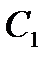 - «поява не більше двох очок»;
- «поява не більше двох очок»;
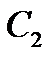 - «поява трьох і чотирьох очок»;
- «поява трьох і чотирьох очок»;
 - «поява не менше п’яти очок».
- «поява не менше п’яти очок».
Г) Випробування – постріл по мішені; події:
 - «влучення»;
- «влучення»;
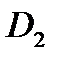 - «промах».
- «промах».
Д) Випробування – два постріли по мішені; події:
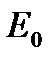 - «жодного влучення»;
- «жодного влучення»;
 - «одне влучення»;
- «одне влучення»;
 - «два влучення».
- «два влучення».
Є) Випробування – витягування двох карт із колоди; події:
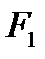 - «поява двох червоних карт»;
- «поява двох червоних карт»;
 - «поява двох чорних карт».
- «поява двох чорних карт».
254. Наведіть приклади:
А) трьох подій, які утворюють простір елементарних подій (випадкових);
Б) трьох подій, рівноможливих і несумісних, але які не утворюють повної групи;
В) двох подій, рівноможливих і таких, що утворюють повну групу, але є сумісними.
255. Знайдіть імовірність того, що при підкиданні двох монет випаде два герба.
256. Серед 4000 перших чисел натурального ряду є 551 просте число. Знайдіть ймовірність того, що навмання взяте натуральне число від 1 до 4000 виявиться простим.
257. Серед 1000 новонароджених було 512 хлопчиків. Знайдіть ймовірність того, що навмання взята новонароджена дитина виявиться хлопчиком.
258. В скриньці 12 білих і 10 чорних кульок. Із скриньки навмання виймають одну кульку. Знайдіть ймовірність того, що ця кулька біла.
259. Уявіть собі, що в групі, в якій ти навчаєшся, розігрується одна безкоштовна туристична подорож до Парижу. З’ясуйте, яка ймовірність того, що в Париж поїдеш саме ти?
260. Щоб скласти іспит з математики, треба вивчити 25 білетів. Студент вивчив на відмінно 20 білетів. Знайдіть ймовірність того, що, відповівши на один білет, він отримає відмінну оцінку?
261. З’ясуйте, яка ймовірність того, що ваша майбутня дитина народиться:
А) 7 числа;
Б) 31 числа;
В) 29 числа?
262. В ящику 45 кульок, з яких 17 білих. Загубили дві не білі кульки. Вкажіть яка ймовірність того, що навмання узята кулька виявиться білою?
263. Вкажіть яка ймовірність того, що навмання узяте двоцифрове число ділиться на 12?
264. У загальноміському святі беруть участь 20 студентів з машинобудівного коледжу, 25 – з залізничного коледжу і 30 – з медичного коледжу. З’ясуйте, яка імовірність того, що студент, з яким ви познайомилися на святі, навчається в залізничному коледжі?
265. З 15 білетів, занумерованих від 1 до 15, навмання вибирають один. Вкажіть яка імовірність того, що номер взятого білета – це число, яке не ділиться ні на 2, ні на 3?
266. З натуральних чисел від 1 до 30 студент навмання називає одне. Вкажіть яка імовірність того, що це число є дільником числа 30?
267. Беруть навмання кісточку доміно. Вона виявилася не дублем. Знайдіть імовірність того, що другу, також узяту навмання кісточку доміно, можна прикласти до першої.
268. Набираючи номер телефону, абонент забув останню цифру і набрав її навмання. Знайдіть імовірність того, що номер набрано правильно. Розв’язати задачу для випадків, якщо остання цифра номера: а) парна; б) не більша від 6.
269. Гральний кубик підкинули один раз. Вкажіть яка імовірність подій: А – випало число, що є дільником числа 4; В – випало не менш ніж 5 очок; С – випало не менш ніж 4 очки; D – випало число, яке є квадратом натурального числа?
270. Вкажіть яка імовірність того, що в березні вибраного року буде п’ять неділь?
271. Маємо новий відривний календар не високосного року. Відриваємо в ньому один листок. Знайдіть імовірність того, що:
А) на листку число 1;
Б) на листку число 31;
С) число на листку ділиться на 3.
272. Знайдіть імовірність отримання дев’яти очок в досліді з двома киданнями грального кубика.
273. Учасники жеребкування беруть з ящика жетони з номерами від 1 до 100. Знайдіть імовірність того, що номер навмання вийнятого жетона не містить цифри 3?
274. Пасажир чекає трамвай 26 або 16 маршруту біля зупинки, де курсують трамваї чотирьох маршрутів: 16, 22, 26, 31. Вважаючи, що трамваї всіх маршрутів проходять однаково часто, знайдіть імовірність того, що перший трамвай, який підійде до зупинки, буде трамваєм потрібного для пасажира маршруту.
275. Із 30 студентів 10 мають спортивні розряди. Знайдіть імовірність того, що три вибрані навмання студенти будуть розрядниками?
276. На кожній із п’яти карток написана одна з літер Т, М, Р, О, Ш. Картки перемішують і розкладають у ряд. Знайдіть імовірність того, що утвориться слово «шторм»?
277. Кожну літеру, що входить у слово «помилка», виписано на окрему картку. Знайдіть імовірність того, що після ретельного перемішування і виймання навмання п’яти карток з них можна буде скласти слово «полка»?
278. У шаховому турнірі беруть участь 20 гравців, яких жеребкуванням поділяють на дві команди по 10 гравців. Знайдіть імовірність того, що 4 найсильніших гравці гратимуть по два у різних командах?
279. Кинуто два гральних кубики. Знайдіть імовірність того, що випадуть різні числа.
280. Знайдіть імовірність того, що у п’ятьох учнів немає спільних днів народження (прийняти, що рік має 365 днів).
281. В урні знаходиться 12 кульок: п’ять білих і сім чорних. Навмання виймають три кульки. Знайдіть ймовірність того, що серед вийнятих кульок:
1) всі три чорні;
2) дві чорні і одна біла;
3) одна чорна і дві білі;
4) всі три білі?
282. Набираючи номер телефону, абонент забув дві останні цифри і, пам’ятаючи лише, що ці цифри різні, набрав їх навмання. Знайдіть ймовірність того, що номер набрано правильно?
283. При грі в «Спортлото» на спеціальній карточці відмічається 6 номерів із 49. Під час тиражу визначаються 6 виграшних номерів. Знайдіть ймовірність вгадати рівно 3 виграшних номера?
284. З озера, де плавають 50 щук, виловили 7 щук, помітили їх і випустили в озеро. Другого разу виловили 12 щук. Знайдіть імовірність того, що серед 12 щук буде дві мічені?
285. Із 16 студентів, серед яких 4 дівчини, на вечір зустрічі без вибору запрошують трьох студентів. Знайдіть імовірність того, що серед запрошених буде одна дівчина?
286. У серії зі 100 виробі є 5 бракованих. Ії партії навмання вибирають 10 виробів. Знайдіть імовірність того, що серед цих 10 виробів буде 2 бракованих?
287. У ліфт 9-поверхового будинку на першому поверсі зайшли 6 чоловік. Знайдіть ймовірність того, що всі вийдуть на різних поверхах, якщо кожний з однаковою ймовірністю може вийти на будь-якому поверсі, починаючи з другого.
288. З 10 лотерейних білетів два виграшних. Знайдіть ймовірність того, що серед узятих будь-яких п’яти білетів:
1) один виграшний;
2) принаймні один виграшний?
289. 9 пасажирів сідають у 3 вагони. Знайдіть ймовірність того, що:
1) у кожний вагон сяде по три пасажири;
2) в один з вагонів сядуть 4, у другий – 3 і в третій – 2 пасажири.
290. Знайдіть ймовірність того, що дні народження 12 чоловік припадають на різні місяці року.
291. Гральний кубик підкидають двічі. Знайдіть ймовірність того, що:
1) у сумі випаде 6 очок;
2) у сумі випаде 7 очок;
3) за два кидки випаде однакова кількість очок;
4) за два кидки випаде різна кількість очок.
292. На десяти однакових картках написано цифри від 0 до 9. З цих карток навмання утворюють двоцифрове число. Знайдіть імовірність таких подій:
А – це число ділиться на 3;
В – це число є дільником числа 99;
С – це число ділиться на 11.
293. У мішку містяться кулі, помічені номерами від 1 до 90. З мішка навмання вибирають 5 куль. Знайдіть імовірність того, що серед вибраних куль буде куля № 90?
294. В урні є 80 номерів, записаних на картках. Кожний учасник лотереї платить 1 гривню і виймає з урни 5 карток. Перед вийманням він записує три задумані номери. Якщо серед вийнятих номерів є три задумані, то учасник виграє 500 гривень. З’ясуйте, чи виграшна ця лотерея для учасника?
295. Випадково взята кісточка доміно виявилася дупелем. Знайдіть імовірність того, що другу, також навмання взяту кісточку, можна приставити до першої?
до змісту
|
|
Дата добавления: 2014-11-29; Просмотров: 3101; Нарушение авторских прав?; Мы поможем в написании вашей работы!