Маршруты, цепи, циклы

Некоторые виды графов

Определение. Граф 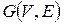такой, что любые две его вершины смежны, называется полным графом. Полный граф с р вершинами обозначается . На рис. 6 показаны графы .

Рис. 6

Степень каждой вершины графа К_р равна 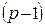. Следовательно, число ребер графа К_р равно .

Определение. Граф 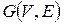называется регулярным степени k, если все его вершины имеют одну и туже степень k. На рис. 7 приведены примеры регулярных графов степени 3. Всякий полный граф К_р – это регулярный граф степени .

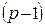Рис.7

Определение. Граф с пустым множеством ребер называется вполне несвязным графом. Вполне несвязный граф с р вершинами будем обозначать через N_p. Граф N ₁, состоящий из единственной вершины, называется тривиальным графом.

Определение. Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны.

В случае простого графа маршрут однозначно определяется последовательностью вершин или последовательностью ребер. Если маршрут в простом графе задан последовательностью вершин v ₀, v ₁ ,, …, v_k, то вершины v ₀, v_k называют концами маршрута. Если v ₀ = v_k, то маршрут называют замкнутым, в противном случае – незамкнутым.

Определение. Маршрут, в котором нет повторений ребер, называется цепью. Цепь, в которой все вершины различны, кроме, может быть, ее концов называется простой. Замкнутая простая цепь называется простымциклом. Про цепь говорят, что она соединяет свои концы.

Определение. Простой цикл с р вершинами обозначается С_р . Например, граф – это одновременно граф С₃.

Определение. Ориентированная простая цепь называется путем, ориентированный простой цикл называют контуром.

Рассмотрим граф на рис. 11. Маршруты в этом графе будем задавать последовательностью вершин.

Пример маршрута: 1 – 2 – 3 – 5 – 7 – 4 – 3 – 5 – 6 – 2 – 3 – 4.

Пример замкнутого маршрута: 3 – 4 – 5 – 7 – 3 – 4 – 1 – 3.

Пример цепи, соединяющий вершины 6 и 8: 6 – 5 – 3 – 4 – 5 – 7 – 3 – 2 – 6 – 8.

Пример цикла: 5 – 3 – 2 – 6 – 5 – 7 – 4 – 5.

Примеры простых цепей, соединяющих вершины 1 и 6: 1 – 3 – 4 – 5 – 6; 1 – 2 – 6; 1 – 4 – 7 – 8 – 6.

Примеры простых циклов: 3 – 5 – 7 – 4 – 3; 1 – 2 – 6 – 8 – 7 – 4 – 1;

1 – 2 – 6 – 5 – 7 – 3 – 1.

Рис. 11

Рассмотрим ориентированный граф на рис. 12. Ориентированные маршруты в этом графе будем задавать последовательностью вершин, проходимых в направлении ориентации дуг.

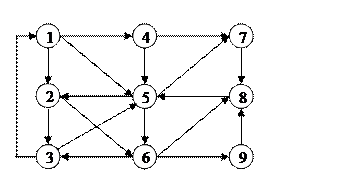
Рис. 12

Пример ориентированного маршрута: 1 ® 2 ® 3 ® 5 ® 2 ® 6 ® 8 ® 5.

Пример замкнутого ориентированного маршрута: 1 ® 4 ® 5 ® 2 ® 6 ® 8 ® 5 ® 2 ® 3 ® 1.

Пример ориентированной цепи: 4 ® 5 ® 7 ® 8 ®5 ® 2.

Пример замкнутой ориентированной цепи: 6 ® 8 ® 5 ® 2 ® 3 ® 1 ® 5 ® 6.

Пример пути, соединяющего вершины 3 и 9: 3 ® 1 ® 4 ® 5® 6 ® 9.

Пример контура: 5 ® 7 ® 4 ® 5.

Дата добавления: 2014-12-07