Проводниковые материалы

РАСЧЕТНЫЕ ФОРМУЛЫ

Плотность тока в проводнике с одним типом носителей заряда

где γ - удельная электрическая проводимость, См*м^-1; E = U/l - напряжен­ность электрического поля в проводнике длиной l, м, при разности потен­циалов между его концами U, В.

Удельная электрическая проводимость металла

где n - концентрация свободных электронов, м^-3; е = 1,6*10^-19 Кл – заряд электрона; μ = v/Е - подвижность электронов, м² /(В*с); v - скорость, приобретаемая электронами в электрическом поле, м/с.

Удельное электрическое сопротивление - это величина, обратная удельной электрической проводимости

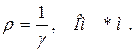
В соответствии с классической электронной теорией металлов выра­жение для удельного электрического сопротивления имеет вид

где m₀ = 0,91*10^-30 кг - масса электрона; 1_ср - средняя длина свободного пробега электронов, м; v_T - средняя скорость теплового движения электро­нов, м/с, которая определяется из соотношения

где k = 1,38*10^-23 Дж/К - постоянная Больцмана, Т - температура, К.

Если атомы в металле ионизированы однократно, то концентрация свободных электронов n будет равна концентрации атомов N и может быть рассчитана по формуле

где d - плотность вещества, кг/м³; М - молярная масса, кг/моль; N_A = 6,02*10²³ 1/моль - постоянная Авогадро.

В соответствии с квантовой теорией удельное электрическое сопро­тивление металлов

где h = 6,63*10^-34 Дж*с - постоянная Планка.

Средняя скорость дрейфа за время свободного пробега

где τ₀ – время свободного пробега.

Среднюю скорость можно также найти по формулам

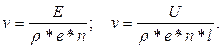
В промежутках между столкновениями с узлами кристаллической решетки электрон при воздействии электрического поля движется с ускорением

а = e*E/m₀.

Удельная проводимость проводника может быть определена как

g = (e² * n * l)/(m₀ * u),

где u – средняя скорость теплового движения (температуре 300 К соответствует средняя скорость порядка 10⁵ м/с).

Время дрейфа электрона по проводнику t = l/v.

Время пролета при движении электрона без соударений t_пр = .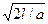

Влияние примесей и структурных дефектов на удельное сопро­тивление. Примеси и структурные дефекты увеличивают удельное сопро­тивление металлов. В соответствии с правилом Маттиссена

ρ = ρ_т + ρ_ост, Ом*м,

где ρ_т - удельное электрическое сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов кристаллической решетки;

ρ_ост = ρ_пр + ρ_деф - остаточное удельное сопротивление, обу­словленное рассеянием электронов на статических дефектах структуры: примесных атомах (ρ_пр) и собственных дефектах структуры (ρ_деф).

Наибо­лее существенный вклад в остаточное сопротивление вносит рассеяние на примесях. При малом содержании примесей удельное сопротивление воз­растает пропорционально концентрации примесных атомов. Кроме приме­сей, некоторый вклад в остаточное сопротивление вносят собственные де­фекты структуры - вакансии, атомы внедрения, дислокации, границы зе­рен. Остаточное сопротивление представляет собой характеристику хими­ческой чистоты и структурного совершенства металла. Для оценки содер­жания примесей измеряют отношение удельного сопротивления металла при комнатной температуре и температуре жидкого гелия: β = ρ₃₀₀/ρ_4,2.

Удельное сопротивление металлических сплавов, имеющих струк­туру неупорядоченного твердого раствора, ρ_ост может существенно пре­вышать ρ_т. Для многих двухкомпонентных сплавов металлов, не принад­лежащих к числу переходных или редкоземельных элементов, зависимость ρ_ост от состава описывается законом Нордгейма

ρ_ост = CX_AX_B = CX_А(1 - X_B), Ом*м,

где C - константа, зависящая от природы сплава; X_A, X_B - атомные доли компонентов в сплаве.

Влияние температуры на сопротивление и длину проводника. В диапа­зоне температур, где зависимость ρ от Т близка к линейной, справедливо выражение

ρ = ρ₀[1 + α_ρ(T – T₀)], Ом*м,

где ρ₀ - удельное сопротивление в начале температурного диапазона;

- средний температурный коэффициент удельного сопротивления в данном диапазоне температур, К^-1;

ρ - удельное сопро­тивление при температуре Т.

Температурные коэффициенты удельного сопротивления a_r, сопротивления a_R и удлинения a_l связаны соотношением

a_r = a_R + a_l.

Температурный коэффициент сопротивления

a_R = (R₂ – R₁)/[R₁ * (T₂ – T₁)].

Зависимость длины проводника от температуры

l = l₀ * [1 + a_l * (T – T₀)],

где l₀ – начальная длина проводника при температуре Т₀;

l – длина при температуре Т;

α_l – температурный коэффициент линейного удлинения.

Теплопроводность металлов. В металлах благодаря высокой кон­центрации свободных электронов преобладает электронная теплопровод­ность. Экспериментальный закон Видемана – Франца - Лоренца устанавливает связь между удельной теплопроводностью λ, Вт*м/К, и удельной электрической проводимостью γ, См/м:

l/g = L₀T,

где L₀ – число Лоренца.

Количество теплоты Q, выделяющееся в единицу времени в единице объема проводника, по которому протекает ток плотностью J, при напряженности электрического поля E, выражается формулой

Q = J*E = γ*E², Вт/м^-3.

Внутренняя контактная разность потенциалов при соприкосновении металлов А и В

eU_k = W_FB - W_FA,

причем уровни Ферми отсчитываются от дна зоны проводимости.

Связь между концентрацией электронов и энергией Ферми

n = (8p/3) * (2m₀/h²)^3/2 * (W_F)^3/2

Разность потенциалов на концах последовательной разнородной цепи

E = (А_н – А_к)/(e*l),

где А_н, А_к – работа выхода электронов из начального и конечного проводников; l – расстояние между ними.

Примечание: если работа выхода выражена в эВ, величина е в знаменателе отсутствует.

Термоэлектродвижущая сила (термоЭДС). В однородном провод­нике при наличии градиента температуры на его концах возникает раз­ность потенциалов. Ее значение, отнесенное к единичной разности темпе­ратур на концах проводника, называют абсолютной удельной термоЭДС. В термоэлектрической цепи, составленной из разнородных проводников (термопаре), относительная удельная термоЭДС представляет собой разность абсолютных удельных термоЭДС составляющих провод­ников

где α_Т^А и α_Т^В - абсолютные удельные термоЭДС контактирующих метал­лов А и В.

Сопротивление проводников на высоких частотах. На высоких частотах наблюдается неравномерное распределение электрического тока по сечению проводника: плотность тока максимальна на поверхности и убывает по мере проникновения вглубь проводника. Распределение тока по сечению проводника описывается уравнением

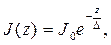
где J₀ - плотность тока на поверхности;

z - координата по нормали к поверхности в глубь проводника, м;

Δ - глубина проникновения поля в проводник, м.

Плотность тока изменяется по тому же закону, что и напряженность электрического поля E, так как J = γE. Связь глубины проникновения поля с физическими характеристиками вещества определяется выражением

где μ₀ = 4π*10^-7 Гн/м - магнитная постоянная;

μ - относительная магнит­ная проницаемость вещества;

f - частота, Гц.

Так как центральная часть сечения проводника почти не использует­ся, активное сопротивление провода R_~ при прохождении по нему пере­менного тока больше, чем его активное сопротивление R₀ при постоянном токе. Коэффициент увеличения сопротивления k_R рассчитывается по фор­муле

,

где S₀ - площадь поперечного сечения проводника, м²;

S_e - эквивалентная площадь сечения проводника, занятая током при воздействии высокочас­тотного поля (для круглого проводника S_e = πdΔ, для плоского - S_e = bΔ, где d - диаметр круглого проводника, м; b - ширина плоского проводника, м).

Дата добавления: 2014-12-07