Билет №29

«Физические характеристики вибрации»

Вибрация – механические колебания упругих тел при низких частотах (1 – 100 Гц), передаются на человека через конструкцию машин, фундамент, пол.

Основными параметрами вибраций, происходивши по синусоидальному закону, являются: амплитуда виброперемещения х_т, амплитуда колебательной скорости v_m, амплитуда колебательного ускорения а_т, период колебаний Т, частота f, связанная с периодом колебаний соотношением f=1/Т.

Вибросмещение в случае синусоидальных колебаний определяют по формуле x=x_msin(wt+j), где w — угловая частота (w = 2pf); j — начальная фаза вибросмещения. В большинстве случаев начальная фаза в задачах охраны труда значения не имеет и может не учитываться.

В общем случае физическая величина, характеризующая вибрацию (например, виброскорость), является некоторой функцией времени: v=v(t) - Математическая теория показывает, что такой процесс можно представить в виде суммы бесконечно длящихся синусоидальных колебаний с различными периодами и амплитудами. В случае периодического процесса частоты этих составляющих кратны основной частоте процесса: f_n=nf₁ (n =1, 2, 3,..., f₁ —основная частота процесса).

Амплитуды гармоник определяют по известным формулам разложения в ряд Фурье. Если же процесс не имеет определенного периода (случайные или кратковременные одиночные процессы), то число таких синусоидальных составляющих становится бесконечно большим, а их частоты распределяются непрерывным образом, при этом амплитуды определяют разложением по формуле интеграла Фурье.

Таким образом, спектр периодического или квазипериодического колебательного процесса является дискретным (рис. 34, а, б), а случайного или кратковременного одиночного процесса — непрерывным (рис. 34,в), Чаще всего в дискретном спектре наиболее ярко выражена основная частота колебаний. Если процесс представляет собой сложение нескольких периодических процессов, частоты отдельных составляющих в его спектре могут быть не кратными друг другу, т. е. имеет место квазипериодический процесс (рис. 34,6). Если же процесс есть результат суммирования нескольких периодических и случайных процессов, спектр его является смешанным, т. е. изображается в виде непрерывного и дискретного спектров, наложенных друг на друга.

В силу специфических свойств органов чувств определяющими являются действующие значения параметров, характеризующих вибрацию. Так, действующее значение виброскорости есть среднеквадратичное мгновенных значений скорости v(t) за время усреднения T_y которое выбирают с учетом характера изменения виброскорости во времени:

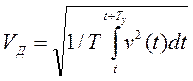
Таким образом, для характеристики вибрации используют спектры действующих значений параметров или средних квадратов последних 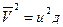. При оценке суммарного воздействия колебаний различных частот или отдельных источников следует иметь в виду, что при сложении некогерентных колебаний результирующую виброскорость (ускорение, смещение) находят соответствующим суммированием мощностей отдельных составляющих спектра (или отдельных источников) или, что одно и то же, суммированием средних квадратов виброскорости 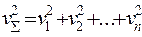, где п — число составляющих в спектре. В соответствии с этим результирующее действующее значение указанного параметра определяется выражением

.

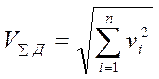Изображение непрерывного спектра требует обязательной оговорки о ширине Df элементарных частотных полос, к которым относится изображение. Если f₁ — нижняя граничная частота данной полосы частот, f₂ — верхняя граничная частота, то в качестве частоты, характеризующей полосу в целом, берется среднегеометрическая частота

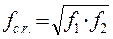
В практике виброакустических исследований весь диапазон частот вибраций разбивают на октавные диапазоны. В октавном диапазоне верхняя граничная частота вдвое больше нижней f₂/f₁=2. Анализ и построение спектров Параметров вибрации могут производиться также в третьоктавных 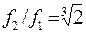полосах частот.

В третьоктаве 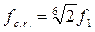. Среднегеометрические частоты октавных полос частот вибраций стандартизованы и составляют 1, 2, 4, 16, 31,5, 63, 125, 250, 500, 1000 Гц.

Учитывая, что абсолютные значения параметров, характеризующих вибрацию, изменяются в очень широких пределах, в практике виброакустических исследований используют понятие логарифмического уровня колебаний. Логарифмический уровень колебаний — характеристика колебаний, сравнивающая две одноименные физические величины, пропорциональные десятичному логарифму отношения оцениваемой и исходного значения величины. В качестве последнего в охране труда используются опорные значения параметров, принятые за начало отсчета. Измеряются уровни в децибелах (дБ). Уровень виброскорости определяют по формуле

,

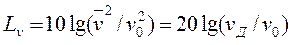где 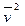— средний квадрат виброскорости берется в соответствующей полосе частот; v₀ — пороговое значение виброскорости, м/с, равное 5-10^-8 м/с, стандартизованное в международном масштабе.

Спектры уровней виброскорости являются основными характеристиками вибраций. Снижение уровня вибраций определяют разностью 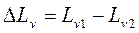, где L_v1 и L_v2 — соответственно уровни вибраций до и после проведения мероприятий по их уменьшению.

Дата добавления: 2014-12-07