Solution. Figure 5. Floating ball problem

Figure 5. Floating ball problem

Figure 1: Geometrical representation of the Secant method

Example 1:

You are working for ‘DOWN THE TOILET COMPANY’ that makes floats for ABC commodes. The ball has a specific gravity of 0.6 and has a radius of 5.5 cm. You are asked to find the distance to which the ball will get submerged when floating in water.

The equation that gives the depth x to which the ball is submerged under water is given by

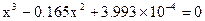
Use the secant method of finding roots of equations to find

a) the depth x to which the ball is submerged under water. Conduct three iterations to estimate the root of the above equation.

b) find the absolute relative approximate error at the end of each iteration, and

c) the number of significant digits at least correct at the end of each iteration.

Let us assume the initial guesses of the root of as and

Iteration #1

The estimate of the root is

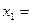
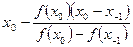
= 0.06461

The absolute relative approximate error, at the end of iteration #1 is

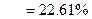
The number of significant digits at least correct is 0, as you need an absolute relative approximate error of at less than 5% for one significant digit to be correct in your result.

Iteration #2

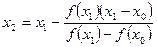
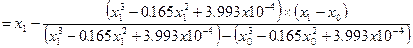
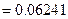
The absolute relative approximate error, at the end of iteration #1 is

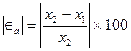
= 3.525%

The number of significant digits at least correct is 1, as you need an absolute relative approximate error of less than 5%.

Iteration #3

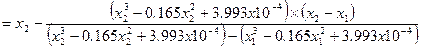
The absolute relative approximate error, at the end of iteration #1 is

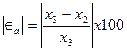
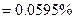
The number of significant digits at least correct is 1, as you need an absolute relative approximate error is at least 5%.

Дата добавления: 2014-12-27