
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод наименьших квадратов для линейной функции
|
|
|
|
Начнем с задачи точечного и доверительного оценивания линейной прогностической функции одной переменной.
Исходные данные – набор n пар чисел (tk , xk), k = 1,2,…,n, где tk – независимая переменная (например, время), а xk – зависимая (например, индекс инфляции, курс доллара США, объем месячного производства или размер дневной выручки торговой точки). Предполагается, что переменные связаны зависимостью
xk = a (tk - tср)+ b + ek , k = 1,2,…,n,
где a и b – параметры, неизвестные исследователю и подлежащие оцениванию, а e k – погрешности, искажающие зависимость. Среднее арифметическое моментов времени
tср = (t1 + t2 +…+tn) / n
введено в модель для облегчения дальнейших выкладок.
Обычно оценивают параметры a и b линейной зависимости методом наименьших квадратов. Затем восстановленную зависимость используют для точечного и интервального прогнозирования.
Как известно, метод наименьших квадратов был разработан великим немецким математиком К. Гауссом в 1794 г. Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость x от t, следует рассмотреть функцию двух переменных

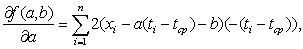
Оценки метода наименьших квадратов - это такие значения a* и b*, при которых функция f(a,b) достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b) по аргументам a и b, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:

Преобразуем правые части полученных соотношений. Вынесем за знак суммы общие множители 2 и (-1). Затем рассмотрим слагаемые. Раскроем скобки в первом выражении, получим, что каждое слагаемое разбивается на три. Во втором выражении также каждое слагаемое есть сумма трех. Значит, каждая из сумм разбивается на три суммы. Имеем:
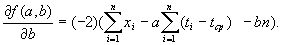

Приравняем частные производные 0. Тогда в полученных уравнениях можно сократить множитель (-2). Поскольку
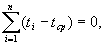 (1)
(1)
уравнения приобретают вид

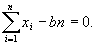
Следовательно, оценки метода наименьших квадратов имеют вид
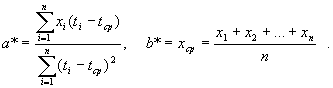 (2)
(2)
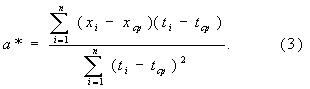
В силу соотношения (1) оценку а* можно записать в более симметричном виде:
Эту оценку нетрудно преобразовать и к виду

Следовательно, восстановленная функция, с помощью которой можно прогнозировать и интерполировать, имеет вид
x*(t) = a*(t - tср)+ b*.
Обратим внимание на то, что использование tср в последней формуле ничуть не ограничивает ее общность. Сравним с моделью вида
xk = c tk+ d + ek , k = 1,2,…,n.
Ясно, что
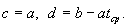
Аналогичным образом связаны оценки параметров:

Для получения оценок параметров и прогностической формулы нет необходимости обращаться к какой-либо вероятностной модели. Однако для того, чтобы изучать погрешности оценок параметров и восстановленной функции, т.е. строить доверительные интервалы для a*, b* и x*(t), подобная модель необходима.
Непараметрическая вероятностная модель. Пусть значения независимой переменной t детерминированы, а погрешности ek, k = 1,2,…,n, - независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией 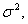 неизвестной исследователю.
неизвестной исследователю.
В дальнейшем неоднократно будем использовать Центральную Предельную Теорему (ЦПТ) теории вероятностей для величин ek , k = 1,2,…,n (с весами), поэтому для выполнения ее условий необходимо предположить, например, что погрешности ek , k = 1,2,…,n, финитны или имеют конечный третий абсолютный момент. Однако заострять внимание на этих внутриматематических "условиях регулярности" нет необходимости.
Асимптотические распределения оценок параметров. Из формулы (2) следует, что
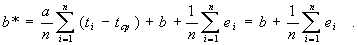 (5)
(5)
Согласно ЦПТ оценка b* имеет асимптотически нормальное распределение с математическим ожиданием b и дисперсией 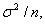 оценка которой приводится ниже.
оценка которой приводится ниже.

Из формул (2) и (5) вытекает, что
Последнее слагаемое во втором соотношении при суммировании по i обращается в 0, поэтому из формул (2-4) следует, что
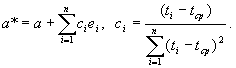 (6)
(6)
Формула (6) показывает, что оценка 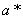 является асимптотически нормальной с математическим ожиданием
является асимптотически нормальной с математическим ожиданием 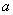 и дисперсией
и дисперсией
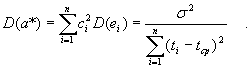
Отметим, что многомерная нормальность имеет быть, когда каждое слагаемое в формуле (6) мало сравнительно со всей суммой, т.е.

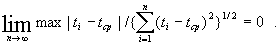

Из формул (5) и (6) и исходных предположений о погрешностях вытекает также несмещенность оценок параметров.
Несмещенность и асимптотическая нормальность оценок метода наименьших квадратов позволяют легко указывать для них асимптотические доверительные границы (аналогично границам в предыдущей главе) и проверять статистические гипотезы, например, о равенстве определенным значениям, прежде всего 0.
Асимптотическое распределение прогностической функции. Из формул (5) и (6) следует, что

т.е. рассматриваемая оценка прогностической функции является несмещенной. Поэтому
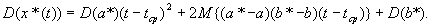
При этом, поскольку погрешности независимы в совокупности и  , то
, то

Таким образом,
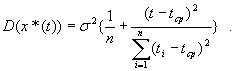
Итак, оценка 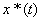 является несмещенной и асимптотически нормальной. Для ее практического использования необходимо уметь оценивать остаточную дисперсию
является несмещенной и асимптотически нормальной. Для ее практического использования необходимо уметь оценивать остаточную дисперсию 
Оценивание остаточной дисперсии. В точках tk , k = 1,2,…,n, имеются исходные значения зависимой переменной xk и восстановленные значения x*(tk). Рассмотрим остаточную сумму квадратов

В соответствии с формулами (5) и (6)

Найдем математическое ожидание каждого из слагаемых:
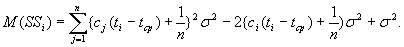
Из сделанных ранее предположений вытекает, что при 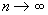 имеем
имеем  следовательно, по закону больших чисел статистика
следовательно, по закону больших чисел статистика  SS/n является состоятельной оценкой остаточной дисперсии
SS/n является состоятельной оценкой остаточной дисперсии 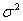 .
.
Получением состоятельной оценкой остаточной дисперсии завершается последовательность задач, связанных с рассматриваемым простейшим вариантом метода наименьших квадратов. Не представляет труда выписывание верхней и нижней границ для прогностической функции:

где погрешность 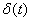 имеет вид
имеет вид

Здесь p - доверительная вероятность, U(p), как и в главе 4 - квантиль нормального распределения порядка (1+р)/2, т.е.

При p= 0,95 (наиболее применяемое значение) имеем U(p) = 1,96. Для других доверительных вероятностей соответствующие значения квантилей можно найти в статистических таблицах (см., например, наилучшее в этой сфере издание [9]).
Сравнение параметрического и непараметрического подходов. Во многих литературных источниках рассматривается параметрическая вероятностная модель метода наименьших квадратов. В ней предполагается, что погрешности имеют нормальное распределение. Это предположение позволяет математически строго получить ряд выводов. Так, распределения статистик вычисляются точно, а не в асимптотике, соответственно вместо квантилей нормального распределения используются квантили распределения Стьюдента, а остаточная сумма квадратов SS делится не на n, а на (n-2). Ясно, что при росте объема данных различия стираются.
Рассмотренный выше непараметрический подход не использует нереалистическое предположение о нормальности погрешностей. Распределения, встречающиеся в задачах менеджмента, как правило, не являются нормальными [1]. Платой за отказ от нормальности является асимптотический характер результатов. В случае простейшей модели метода наименьших квадратов оба подхода дают практически совпадающие рекомендации. Это не всегда так, не всегда два подхода бают близкие результаты. Например, в задаче обнаружения выбросов методы, опирающиеся на нормальное распределение, нельзя считать обоснованными, и обнаружено это было с помощью непараметрического подхода [1].
Общие принципы. Кратко сформулируем несколько общих принципов построения, описания и использования эконометрических методов анализа данных. Во-первых, должны быть четко сформулированы исходные предпосылки, т.е. полностью описана используемая вероятностно-статистическая модель. Во-вторых, не следует принимать предпосылки, которые редко выполняются на практике. В-третьих, алгоритмы расчетов должны быть корректны с точки зрения математико-статистической теории. В-четвертых, алгоритмы должны давать полезные для практики выводы.
Применительно к задаче восстановления зависимостей это означает, что целесообразно применять непараметрический подход, что и сделано выше.
Пример оценивания по методу наименьших квадратов. Пусть даны n = 6 пар чисел (tk , xk), k = 1,2,…,6, представленных во втором и третьем столбцах табл.1. В соответствии с формулами (2) и (4) выше для вычисления оценок метода наименьших квадратов достаточно найти суммы выражений, представленных в четвертом и пятом столбцах табл.1.
Таблица 1.
Расчет по методу наименьших квадратов при построении линейной прогностической функции одной переменной
| i | ti | xi | 
| 
| 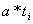
| 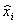
| 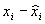
| (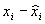 )2 )2
|
| 3,14 | 12,17 | -0,17 | 0,03 | |||||
| 9,42 | 18,45 | 1,55 | 2,40 | |||||
| 12,56 | 21,59 | -1,59 | 2,53 | |||||
| 21,98 | 31,01 | 0,99 | 0,98 | |||||
| 28,26 | 37,29 | -2,29 | 5,24 | |||||
| 31,40 | 40,43 | 1,57 | 2,46 | |||||
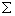
| 0,06 | 13,64 | ||||||

| 5,67 | 26,83 | 42,67 | 185,17 |
В соответствии с формулой (2) b* =26,83, а согласно формуле (4)

Следовательно, прогностическая формула имеет вид

Следующий этап анализа данных - оценка точности приближения функции методом наименьших квадратов. Сначала рассматриваются т.н. восстановленные значения

Это те значения, которые полученная в результате расчетов прогностическая функция принимает в тех точках, в которых известны истинные значения зависимой переменной xi.
Вполне естественно сравнить восстановленные и истинные значения. Это и сделано в шестом - восьмом столбцах табл. 1. Для простоты расчетов в шестом столбце представлены произведения 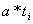 , седьмой отличается от шестого добавлением константы 9,03 и содержит восстановленные значения. Восьмой столбец - это разность третьего и седьмого.
, седьмой отличается от шестого добавлением константы 9,03 и содержит восстановленные значения. Восьмой столбец - это разность третьего и седьмого.
Непосредственный анализ восьмого столбца табл.1 показывает, что содержащиеся в нем числа сравнительно невелики по величине по сравнению с третьим столбцом (на порядок меньше по величине). Кроме того, знаки "+" и "-" чередуются. Эти два признака свидетельствуют о правильности расчетов. При использовании метода наименьших квадратов знаки не всегда чередуются. Однако если сначала идут только плюсы, а потом только минусы (или наоборот, сначала только минусы, а потом только плюсы), то это верный показатель того, что в вычислениях допущена ошибка.
Верно следующее утверждение.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 505; Нарушение авторских прав?; Мы поможем в написании вашей работы!