Решение задач имитационного моделирования инвестиционных рисков средствами MS Excel

Работы

Методические указания по выполнению контрольной

В мировой практике финансового менеджмента используются различные методы анализа рисков инвестиционных проектов (ИП). Рассмотрим имитационное моделирование.

Имитационное моделирование. Практическое применение данного метода продемонстрировало широкие возможности его использования в инвестиционном проектировании, особенно в условиях неопределённости и риска. Данный метод особенно удобен для практического применения тем, что удачно сочетается с другими экономико-статистическими методами, а также с теорией игр и другими методами исследования операций. Практическое применение авторами данного метода показало, что зачастую он даёт более оптимистичные оценки, чем другие методы, например анализ сценариев, что, очевидно обусловлено перебором промежуточных вариантов.

Многообразие ситуаций неопределённости делает возможным применение любого из описанных методов в качестве инструмента анализа рисков, однако, по мнению авторов, наиболее перспективными для практического использования являются методы сценарного анализа и имитационного моделирования, которые могут быть дополнены или интегрированы в другие методики.

Инструмент «Генерация случайных чисел», предназначен для автоматической генерации множества данных (генеральной совокупности) заданного объема, элементы которого характеризуются определенным распределением вероятностей. При этом могут быть использованы 7 типов распределений: равномерное, нормальное, Бернулли, Пуассона, биномиальное, модельное и дискретное. Применение инструмента «Генератор случайных

чисел», как и большинства используемых в этой работе функций, требует установки специального дополнения «Пакет анализа».

Прежде всего, при имитационном анализе, нас будет интересовать коэффициент вариации ЧСС (NPV) - чистая современная стоимость.

Рассмотрим имитацию с инструментом «Генератор случайных чисел»

Задача 1

Смоделируем следующую ситуацию как показано на рисунке 1. Количество имитаций выставим - 500.

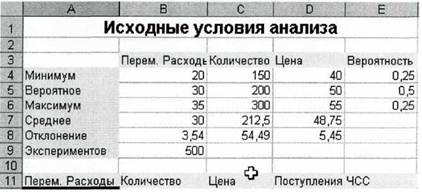
Рис. 1. Исходные данные

1. Постройте в Excel таблицу, как на рис. 1.

2. Установите курсор в ячейку А7.

Приступаем к проведению имитационного эксперимента.

3. Выберите в главном меню «Сервис» пункт «Анализ данных». Если данный пункт отсутствует, то следует выполнить следующую команду Сервис ® Надстройки ® Пакет анализа. Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.

4. Выберите из списка «Инструменты анализа» пункт «Генерация случайных чисел» и нажмите кнопку «ОК» (рис. 2).

Рис. 2. Окно анализа данных

4. На экране появится диалоговое окно «Генерация случайных чисел». Укажите в списке «Распределения» требуемый тип - «Нормальное». Заполните остальные поля изменившегося окна согласно рис. 3 и нажмите кнопку «ОК». Результатом будет заполнение блока ячеек А12-А511 (переменные расходы) сгенерированными случайными значениями.

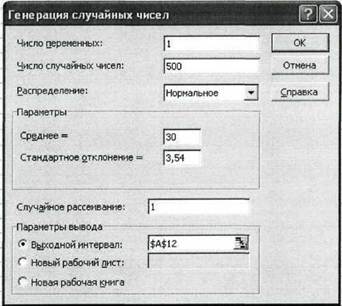
Рис. 3.Диалоговое окно «Генерация случайных чисел» Первым заполняемым аргументом диалогового окна «Генерация случайных чисел» является поле «Число переменных». Оно задает количество колонок таблицы, в которых будут размещаться сгенерированные в соответствии с заданным законом распределения случайные величины. Следующим обязательным аргументом для заполнения является содержимое поля «Число случайных чисел» (т.е. - количество имитаций). Выбранный тип распределения определяет внешний вид диалогового окна. Указание аргумента «Случайное

рассеивание» позволяет при повторных запусках генератора получать те же значения случайных величин, что и при первом. Последний аргумент диалогового окна «Генерация случайных чисел» - «Параметры вывода» определяет место расположения полученных результатов.

Рис. 4. Итоговая таблица

6. Примените пункт «Генерация случайных чисел» для полей «Количество», «Цена», «Поступления» и «ЧСС», используя индивидуальные параметры (Среднее и Отклонение) для каждого из полей (значения параметров приведены в исходной таблице на рис. 1).

7. Для полей «Поступления» и «ЧСС» установите среднее: 1427,71 и 3412,14 соответственно, стандартное отклонение: 674,48 и 2556,87 соответственно.

8. В результате выполненных действий, у вас должна получиться таблица, как на рис. 4.

9. Создайте на пустом листе незаполненную таблицу, как на рис. 5.

Рис. 5. Образец новой таблицы

10. Перейдите на предыдущий лист и выберите пункт меню Сервис ® Анализ данных... ® Описательная Статистика (рис. 6).

Рис. 6. Диалоговое окно «Анализа данных» 11.В открывшемся диалоговом окне ввести значения как на рис. 7.

• Входной интервал: значение поля «Перем.расх.» ($А$12:$А$511);

• Группирование: по столбцам;

• Параметры выхода (выходной интервал): Лист2!$А$2 (т.е. адрес на новом листе).

• Установите метку на параметре: Итоговая статистика.

• Нажмите ОК.

Рис. 7. Диалоговое окно «Описательная статистика»

12. Проделайте ту же работу для полей «Количество», «Цена», «Поступления» и «ЧСС».

13.Отредактируйте полученную таблицу так, чтобы получилось только одно поле с названиями значений, как на рис. 8. В полученной таблице нас будут интересовать выделенные параметры. Значения в таблице не обязательно должны точно совпадать, допускаются некоторые расхождения.

Рис. 8. Итоговый результат задачи 1 Задача 2

В данной задаче найдем с помощью стандартных функций Excel, следующие значения:

• коэффициент вариации ЧСС;

• вероятность того, что ЧСС будет меньше нуля;

• вероятность того, что ЧСС будет больше максимума;

• вероятность того, что ЧСС будет находится в интервале [М(Е) + а;

max];

вероятность того, что ЧСС будет находиться в интервале [М(Е) - а;

1. Дополните таблицу следующими строками: «Коэффициент вариации», «Р(Е<=0)>>, «Р(Е<=МИН (Е))», «Р(М(Е) + а <=Е <= max)», «P(M(E) - а <=Е <=М(Е))>>.

2. Вычисление введенных полей осуществляется по формулам, приведенных в таблице.

Ячейка	Формула
Коэффициент вариации	В6/В2
Р(Е<=0)	НОРМРАСП(0;В2;В6; 1)
Р(Е<=МИН (Е))	НОРМР АСП(В 11;В2;В6; 1)
Р(М(Е) + а <=Е <= max)	НОРМР АСП(В 12;В2;В6; 1)-НОРМР АСП(В2+В6;В2;В6;1)
Р(М(Е) - а <=Е <=М(Е))	НОРМР АСП(В2;В2;В6;1)-НОРМРАСП(В2-В6;В2;В6;1)

Функция НОРМРАСП

НОРМРАСП - возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция имеет очень широкий круг приложений в статистике, включая проверку гипотез.

НОРМРАСП(х;среднее;стандартное_откл;интегральная)

х - значение, для которого строится распределение.

Среднее - среднее арифметическое распределения.

Стандартное_откл - стандартное отклонение распределения.

Интегральная - логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

3. Отформатируйте таблицу в числовом формате (с числом десятичных знаков - 2), конечный результат должен получиться, как на рис. 9.

Рис. 9. Итоговый результат задачи 2

Рассмотрим результаты проведенного имитационного эксперимента: Величина ожидаемой ЧСС (NPV) равна 3386,86 при стандартном отклонении 2567,02. Коэффициент вариации (0,76) несколько высок, но меньше 1, таким образом, риск данного проекта в целом ниже среднего риска инвестиционного портфеля фирмы. Результаты вероятностного анализа показывают, что шанс получить отрицательную величину ЧСС (NPV) не превышает 9%. Общее число отрицательных значений ЧСС (NPV) в выборке составляет 32 из 500. Таким образом, с вероятностью около 91% можно утверждать, что чистая современная стоимость проекта будет больше 0.

Для расчёта цены риска в данном случае используем показатель среднеквадратического отклонения - а, и матожидания - М (NPV). При этом вероятность того, что величина NPV окажется больше чем M(NPV) + а, равна 16% (ячейка F18). Вероятность попадания значения NPV в интервал [M(NPV) -а; M(NPV)] равна 34%.

Дата добавления: 2014-12-27