Адаптивная нормативная система УФО-анализа

Основу любого метода традиционного системного (системно-структурного, структурно-функционального) или объектного анализа составляет некоторая нормативная система. Неотъемлемой частью нормативной системы (как и любой формальной системы) являются алфавит, включающий в себя знаки (символы), используемые для записи по определенным правилам выражений (в данном случае построения диаграмм), а также правила манипулирования этими знаками (в данном случае правила построения диаграмм).

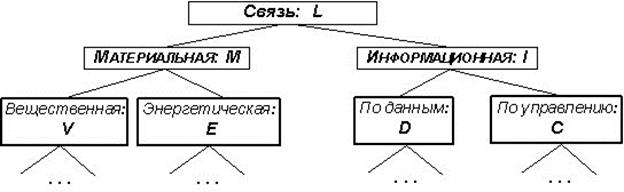
В случае системно-объектного подхода «Узел-Функция-Объект» в качестве алфавита рассматривается набор у злов (перекрестков связей/потоков), набор ф ункций, балансирующих эти узлы, и набор о бъектов, реализующих эти функции. При этом для формирования набора узлов используется классификация, определяемая базовойтаксономической (родовидовой) классификациейсвязей (рис. 5.2) в зависимости от «протекающих» по ним ресурсов.

Классификация связей обеспечивает параметричность классификации узлов и конструктивное определение семантики символов этих узлов. Пример классификации УФО-элементов по их узлам (для бинарного случая) на уровне базовой классификации связей представлен на рисунке 5.3.

Естественно, классификации связей L, узлов (L)L (а также изоморфные последней классификации функций L(L) и объектов Ll, т.е. УФО-элементов) могут быть специализированы с любой степенью точности для любой конкретной предметной области.

В качестве алфавитных элементов могут рассматриваться любые УФО-элементы, получаемые путем комбинирования связей из базовой классификации либо из классификации, представляющей собой результат ее специализации. При этом естественным образом возникают следующие варианты.

1. Система (УФО-элемент) представляет собой объект L^outlⁱⁿ, занимающий узел (Lⁱⁿ)L^out с одним входом и одним выходом и реализующий функцию L^out(Lⁱⁿ) преобразования одного переменного. Данный УФО-элемент называется «элементарным» или «алфавитным». Его элементарность не означает невозможности его дальнейшей декомпозиции.

2. Система (УФО-элемент) представляет собой объект L^outlⁱ (i = 1, …, n), занимающий узел (Lⁱ, …, Lⁿ)L^out с несколькими входами и одним выходом и реализующий функцию L^out(Lⁱ, …, Lⁿ) преобразования нескольких переменных. Данный УФО-элемент является «композицией» нескольких алфавитных элементов, объединенных в одну целостную (эмерджентную) субстанцию в связи с тем, что они обеспечивают одну общую функциональность.

3. Система (УФО-элемент) представляет собой объект Lⁱlⁱⁿ (i = 1, …, n), занимающий узел (Lⁱⁿ)Lⁱ, …, Lⁿ с одним входом и несколькими выходами, обслуживаемыми одним входом, и реализующий функции Lⁱ(Lⁱⁿ), …, Lⁿ(Lⁱⁿ). Данный УФО-элемент является «суперпозицией» разных алфавитных элементов, объединенных в одну субстанцию в связи с одинаковостью входных потоков. Скорее всего, разъединение алфавитных элементов не представляется возможным или целесообразным.

4. Система (УФО-элемент) представляет собой объект L^jlⁱ (i = 1, …, n; j = 1, …, m), занимающий узел (Lⁱ, …, Lⁿ)L^j, …, L^m с несколькими входами и несколькими выходами, реализующий сложную функцию L^j, …, L^m(Lⁱ, …, Lⁿ). Данный УФО-элемент является «агрегацией», состоящей из нескольких функционально независимых элементов, каждый из которых будет экземпляром определенного класса 1-го, и/или 2-го, и/или 3-го типа, описанных выше. В принципе данные функции могут быть выполнены разными элементами.

Классификационный способ задания алфавита формальной (в данном случае – нормативной) системы играет роль алгоритма для задания семантики знаков этой системы, что превращает ее (нормативную систему) в алгоритмически построенную или конструктивную систему. Следовательно, данный способ обеспечивает получение алфавита нормативной системы, обладающего не только совершенно абстрактной или сугубо математической семантикой, но и предметно (проблемно) -ориентированной, что позволяет рассматривать данный алфавит как формально-семантический, а таким же образом саму нормативную систему. При этом реализуются актуальные предложения специалистов по информатике, которые считают, что уже давно «возникла практическая потребность перехода от формально-математического к содержательному анализу информационных феноменов и их «движущей силы» в самоорганизующихся системах социальной природы» [107].

Использование классификации для порождения семантики алфавитных символов обеспечивает еще одну принципиальную отличительную особенность такого алфавита. Как при конечном, так и при бесконечном формальном алфавите количество исходных понятий, соответствующих знакам алфавита обычной формальной системы, является конечным и ограниченным. Это обстоятельство приводит к тому, что совершенно различные предметные области моделируются с помощью одного и того же набора алфавитных символов нормативной системы какого-либо метода традиционного системного анализа. Задание же алфавита с помощью классификации позволяет изменять количественный и качественный состав исходных понятий и соответствующих алфавитных символов, т.е. адаптировать алфавит (и нормативную систему) в зависимости от исследуемой и моделируемой предметной области.

Таким образом, предложенный способ формирования алфавита (узлов, функций и объектов: УФО-элементов) позволяет использовать при решении каждой конкретной задачи свой конкретный набор средств моделирования, т.е. алфавитных символов. Например, для моделирования информационного бизнеса (организационных систем – средств массовой информации) можно уточнить до соответствующих конкретных классов классы, связанные с информационными связями, а классы, связанные с веществом и энергией оставить в виде абстрактных классов; для моделирования электроэнергетических предприятий необходимо конкретизировать классы, связанные с энергетическими связями; для моделирования транспортных компаний – классы с вещественными связями; для моделирования производства – классы, моделирующие получение вещества соответствующего вида. Незыблемым остается лишь принцип, в соответствии с которым свойства объектов (функций и узлов), используемых для создания модели, определяются их параметрической таксономической классификацией, т.е. базовой классификации классов, учитывающей эти свойства.

Придание алфавиту нормативной системы предметно-ориентированной семантики и свойства адаптивности улучшает ее интерпретационные характеристики и упрощает ее использование для моделирования в различных конкретных ситуациях. Однако, это не снижает степени формальности такой нормативной системы, так как при условии алгоритмического задания семантики и синтаксиса она будет удовлетворять всем требованиям, предъявляемым к формальной системе с точки зрения явного и строгого описание средствами самой формальной системы всех свойств и отношений всех используемых символов, а также с точки зрения распознавания всех символов только по их форме.

При этом обеспечивается возможность объективной (обоснованной) декомпозиции организационной системы (бизнес-системы), и даже возможность передачи, например, компьютерной информационной системе поддержки бизнеса (реинжиниринга бизнеса) формально-логических редакторских и контрольных функций при создании моделей и управлении ими.

Декомпозиция системы, осуществляемая, например, в ходе ООА, помимо выявления структуры классов, направлена также на выявление структуры объектов моделируемой системы и построение объектной модели. Следовательно, необходимо задать определенные правила манипулирования символами алфавита для построения объектных моделей, что, собственно, и обеспечит превращение получаемого с помощью предложенной иерархии классов алфавита в нормативную систему.

Так как символы предложенного алфавита по определению представляют собой различные системные компоненты (узлы, функции, объекты), то, следовательно, правила оперирования этими символами должны быть основаны на системных отношениях, рассматриваемых в рамках выбранного системного подхода. Как известно, функциональная системология рассматривает в качестве основного системного отношения отношение поддержания функциональной способности целого [5; см. также п. 2.3]. Это позволяет сформулировать в качестве основного правила оперирования символами алфавита системных компонент закон системной декомпозиции: «Элементы на i-ом ярусе системы должны находиться в отношении поддержания функциональной способности i+1-го яруса системы (системы должны поддерживать надсистему, подсистемы – систему и т.д.)».

Соблюдение данного закона обеспечивается путем выполнения следующих правил системной декомпозиции, естественным образом вытекающих из положений функциональной системологии:

1. Правило присоединения: элементы должны присоединяться друг к другу в соответствии с качественными и количественными характеристиками присущих им связей;

2. Правило баланса: при присоединении элементов друг к другу (в соответствии с правилом 1) должен обеспечиваться качественный и количественный баланс «притока» и «оттока» по входящим и выходящим функциональным связям;

3. Правило реализации: при присоединении элементов друг к другу (в соответствии с правилами 1 и 2) должно быть обеспечено соответствие интерфейсов и объектных характеристик функциональным;

4. Правило замкнутости: внутренние (поддерживающие) связи/потоки элементов в системе должны быть замкнутыми.

Данные правила позволяют собирать из УФО-элементов модели различной сложности, которые называются УФО-конфигурациями. При этом инструментарий УФО-подхода (см. далее) позволяет определять более правильные конфигурации и рационализировать, например, процедуру организационного проектирования бизнес-системы.

Таким образом, предложен алфавит, необходимый для построения моделей организационных систем, который вместе со сформулированными правилами системной декомпозиции представляет собой нормативную систему, особенности которой заключаются в том, что она:

- объективизирует процесс декомпозиции объектов и классов организационной системы;

- предоставляет для каждого вида организационной системы (бизнеса) свою номенклатуру функциональных объектов (алфавитных символов), формируемую по единому принципу;

- обеспечивает имитацию понимания компьютером свойств классов и экземпляров объектной модели.

Построенная таким образом нормативная система, описываемая адаптивным (гибким, динамическим) алфавитом, обладающим содержательной (но однозначной) семантикой, позволяет реализовать новый метод анализа и моделирования организационных систем – УФО-анализ.

Дата добавления: 2014-12-27