Стандартные интервалы???

Вопрос 7. Генеральная совокупность и выборка. Объем выборки. Репрезентативность.

Генеральная совокупность - это множество всех мыслимых значений наблюдений, однородных относительно некоторого признака, которые могли быть сделаны.

Объем генеральной совокупности N.

Выборка – совокупность случайно отобранных наблюдений для непосредственного изучения из генеральной совокупности.

Выборка характеризуется:

– варианта- каждый элемент выборки.

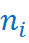- частота встречаемости- число наблюдений варианты.

Объем выборки - это количественная характеристика выборки. Это количество вариант в выборке. Это число случаев, включенных в выборочную совокупность.

Репрезентативность (фр. Representative - представляющий) - это соответствие характеристик выборки характеристикам генеральной совокупности.

Репрезентативность- это свойство выборки представлять параметры генеральной совокупности.

Вопрос 8 Статистическое распределение (вариационный ряд) Гистограмма.

Статистическое распределение - это совокупность вариант и соответствующих им частот .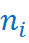

Вариационный ряд - последовательность вариант, записанных в возрастающем порядке.

Гистограмма - это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине класса, а высота равна или частоте попадания в интервал 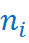или относительной частоте 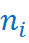/n

Ширину интервала I можно определить по Формуле Стерджеса:

Вопрос 9. Характеристики положения (мода, медиана, выборочная средняя) и рассеяния (выборочная дисперсия и выборочное среднее квадратическое отклонение).

Мода (Мо) – наиболее часто встречающаяся варианта в данной совокупности.

Мода (Мо) - это такое значение варианты, что предшествующие и следующие за ней значения имеют меньшие частоты встречаемости.

Медиана (Ме) - это значение признака, относительно которого вариационный ряд делится на две равные части.

Выборочная средняя – это среднее арифметическое значение вариант статистического ряда:

Характеристики рассеяния определяют отклонение каждой варианты от средней арифметической.

Выборочная дисперсия – это среднее арифметическое квадратов отклонения вариант от их среднего значения:

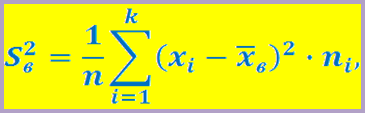
Среднее квадратическое отклонение – стандартное отклонение- квадратный корень из выборочной дисперсии:

n – объем выборки

ni – частота встречаемости

xi – варианта

х – выборочное среднее

Вопрос 10 Оценка параметров генеральной совокупности по характеристикам ее выборки (точечная и интервальная)

Оценка параметра - это любая функция от значений выборки.

Параметры выборки:

1) Выборочное среднее

2) Выборочная дисперсия

Параметры генеральной совокупности:

1) Генеральное среднее

2) Генеральная дисперсия

Точечная оценка - это выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики.

- Определяется одним числом (точкой на числовой оси)

- Выборка должна быть большого объема.

- Дает лишь некоторое приближенное значение параметра.

Требование: несмещенная, состоятельная, эффективная.

Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки.

1) Генеральное среднее равно математическому ожиданию выборочной средней. Следовательно:

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя:

2) Генеральная дисперсия не равна математическому ожиданию выборочной дисперсии.

Следовательно: выборочная дисперсия- это смещенная оценка

генеральной дисперсии.

Тут можно сказать об исправленной дисперсии. (а можно и не сказать)

Исправленная дисперсия (более точная)

Генеральная дисперсия равна математическому ожиданию исправленной дисперсии.

Интервальная оценка - это числовой интервал, содержащий неизвестный параметр генеральной совокупности заданной вероятностью.

- Определяется двумя числами – границами интервала.

- Более точная, надежная и информативная, так как дает информацию о степени близости соответствующему теоретическому параметру.

- Используется, если выборка малого объема.

Вопрос 11. Доверительный интервал и доверительная вероятность.

Доверительный интервал — это интервал, в котором с той или иной заранее заданной вероятностью находится генеральный параметр.

,

(Р≥0,95)

где - генеральное среднее; - выборочное среднее;

-нормированный показатель распределения Стьюдента, с (n-1) степенями свободы, который определяется вероятностью попадания генерального параметра в данный интервал; х- средняя ошибка выборочной средней.

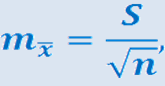
Доверительная вероятность P это такая вероятность, что событие 1-Р можно считать невозможным.

Признана достаточной для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Обычно в качестве доверительных используют вероятности, близкие к 1. Тогда событие, что генеральный параметр попадет в этот интервал будет практически достоверным.

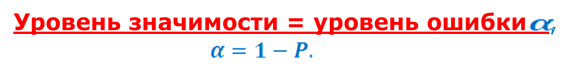
Вопрос 12 сравнение средних значений двух нормально распределенных генеральных совокупностей.

Схема проверки гипотезы:

1) Выдвигаем нулевую гипотезу H0. Это основная гипотеза.

Сущность H0: разница между сравниваемыми генеральными параметрами = 0, и различия, наблюдаемые между выборочными данными носят случайный характер.

или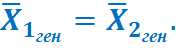

2) Формулируем альтернативную гипотезу Н1 конкурирующую с Н0. Это логическое отрицание Н0.

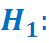
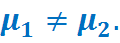
3) Задаем уровень значимости критерия.

Уровень значимости критерия а - это вероятность ошибки отвергнуть Н0, если на самом деле она верна.

4) Для проверки нулевой гипотезы можно использовать параметрический критерий Стьюдента сравнения средних.

Величину критерия находим по формуле:

Обычно расчет ведется на ЭВМ.

Это отношение имеет t-распределение Стьюдента с степенями свободы.

5) По таблице известного распределения находим

6) Сравниваем

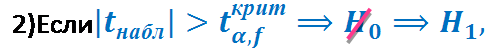
7) Выводы

1)Различие недостоверно.

2)Различие достоверно, значимо

Дата добавления: 2014-12-27