Теоретические положения. Внимание! При достижении 100 °С немедленно отключить печь!

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ТЕМПЕРАТУРЫ НА УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ СПЛАВОВ ВЫСОКОГО СОПРОТИВЛЕНИЯ

Лабораторная работа № 4

Внимание! При достижении 100 °С немедленно отключить печь!

Результаты измерений занести в таблицу 3.3.

Таблица 3.3

t, °С	ха,, мм	Uа, В	уа, мм	Qа, Кл	Сст, Ф

7. По полученным данным построить график зависимостиС_ст = f(t).

8. Составить отчет, который должен содержать:

а) название работы и ее цель;

б) схему установки;

в) основные расчетные формулы;

г) заполненные таблицы 3.1, 3.2 и 3.3;

д) петли гистерезиса для разных напряжений;

е) зависимости Q_а = f(U), С_ст= f(U); Q_r = f(U); tg d = f(U), С_ст = f(t);

ж) вывод.

Вопросы к защите лабораторной работы № 3

1. Что такое сегнетоэлектрик?

2. Нарисовать петлю гистерезиса, назвать основные параметры петли.

3. Нарисовать принципиальную схему установки.

4. Что такое домены?

5. Как определяются масштабы по вертикали и горизонтали?

6. Как определяются потери в сегнетоэлектриках?

7. Нарисовать зависимости Q_а = f(U), С_ст= f(U); Q_r = f(U); tg d = f(U),
С_ст = f(t).

8. Как зависит емкость конденсатора из сегнетоэлектрика от температуры?

9. Где применяются сегнетоэлектрики?

Цель работы: построение зависимостей изменения сопротивления манганина и нихрома от температуры R = f(t), определение по ним зависимостей изменения удельного сопротивления от температуры r = f(t) и температурных коэффициентов сопротивления TK_R = f(t).

Металлические проводники можно разделить на две группы:

1. Металлы высокой проводимости (r 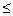0,05 мкОм×м.)

2. Сплавы высокого сопротивления (r > 0,3 мкОм×м.)

Все чистые металлы с наиболее правильной кристаллической решеткой имеют наименьшие значения удельного сопротивления. Любые примеси и нарушения правильной структуры металлов увеличивают их удельное сопротивление. Это свойство металлов широко используется для получения материалов с большим удельным сопротивлением, которые необходимы везде, где нужно получить большое сопротивление при малом объеме. Это, как правило, сплавы.

Сплавы высокого сопротивления классифицируются по области применения [2]:

1) материалы для образцовых сопротивлений и электроизмерительных приборов.

2) материалы для резисторов.

3) материалы для нагревательных приборов и нагрузочных реостатов.

К сплавам высокого сопротивления предъявляют следующие требования:

− большое удельное сопротивление;

− достаточная механическая прочность и технологичность, обеспечивающие возможность получения провода необходимого сечения;

− небольшая стоимость.

К материалам первой группы предъявляются дополнительные требования:

− стабильность сопротивления во времени (отсутствие старения);

− небольшой температурный коэффициент удельного сопротивления (TK_ρ = min);

− маленький коэффициент термоЭДС с медью.

Для третьей группы дополнительное требование – высокая температура нагрева.

Основным материалом первой группы является медно-марганцевый
сплав – манганин (название происходит от наличия в нём марганца – латинское название manganum). Примерный его состав: Cu 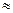85 %, Mn 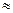12 %, Ni 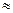3 %.

Основные параметры манганина [2]:

− удельное сопротивление ρ = (42 − 51)×10^-8 Ом∙м;

− температурный коэффициент TK_r= (–5…+30)·10^-5 К^-1;

− коэффициент термоЭДС в паре с медью всего Y = 1 − 2 мкВ/К;

− предел прочности σ_в = 450 − 600 МПа;

− предельная допустимая температура t = 200 ^оС.

Манганин выпускается в виде тонкой проволоки, на которую накладывают эмалево-волокнистую изоляцию.

Основным материалом второй группы является медно-никелевый сплав – константан. Его примерный состав: Ni 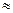39−41 %, Mn 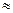1−2 %, остальное
(56−59 %) – Cu.

Для электронагревательных приборов в основном применяются сплавы на основе железа: нихром, фехраль, хромаль.

Основные параметры нихрома [2]:

− удельное сопротивление ρ = (110−120)×10^-8 Ом∙м;

− температурный коэффициент TK_r= (10−20)×10^-5 К^-1;

− предел прочности σ_в = 650−700 МПа;

− предельная допустимая температура t =1000−1100 ^оС.

В лабораторной работе определяются основные электрические характеристики манганина и нихрома. Сначала нужно построить зависимости R = f(t). Их снимают при нагреве катушек из манганина (рис. 4.1) и нихрома в печи от 20 до 300 °С. Параметры катушек приведены в таблице 4.1.

Рис. 4.1. Фотография катушки из манганина

Таблица 4.1

Параметры катушек из манганина и нихрома

Материал проводника катушки	Марка сплава проводника	Диаметр проводника Dп, мм	Площадь сечения проводника Sп, мм^2	Длина проводника ℓ п, м
Манганин	МНМц 3–12	0,10	7,85×10^–3	26,70
Нихром	Х20Н80	0,10	7,85×10^–3	11,80

На рисунке 4.2 приведена фотография установки. Она состоит из следующих блоков:

1) муфельной электрической печи ПМ-8;

2) блока из трех цифровых приборов М890 (один служит для измерения температуры, два других − для измерения сопротивлений);

3) катушек из манганина и нихрома (на рисунке 4.2 не видны, так как находятся в печи);

4) зарядного устройства приборов.

Рис. 4.2. Cтенд для исследования сплавов высокого сопротивления

Обе зависимости R = f(t) строятся одновременно. Это позволяет уменьшить время выполнения лабораторной работы, так как теперь не надо ждать, пока остынет печь. А потом по экспериментальным данным выполняются расчеты и строятся зависимости TK_R = f(t), r = f(t).

По зависимости R = f(t) (рис. 4.3) необходимо вычислить температурный коэффициент сопротивления:

TK_R = ∙ » ∙ ,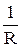

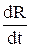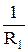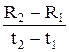где TK_R – температурный коэффициент сопротивления, 1/ 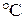; R₂ – сопротивление катушки при температуре t₂; R₁ – сопротивление катушки при температуре t₁ (t₂ > t₁ ).

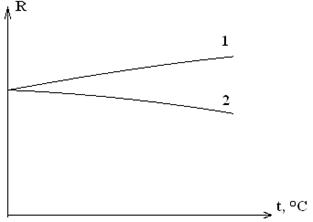
Рис. 4.3. Зависимость R = f(t) для нихрома (1) и манганина (2)

Удельное сопротивление сплава определяется по формуле

r = ,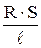

где r – удельное сопротивление в Ом×м;

S – площадь сечения проводника, м²;

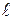– длина проводника катушки, м.

Удельное сопротивление сплава при нагревании изменяется по двум причинам:

1. С ростом температуры увеличивается амплитуда тепловых колебаний атомов, у электронов на пути возникает больше препятствий, уменьшается средняя длина свободного пробега электрона и, как следствие, растет удельное сопротивление. (Этот процесс характеризуется температурным коэффициентом сопротивления TK_R).

2. С ростом температуры проводник расширяется, в результате уменьшается его плотность, что приводит к дополнительному увеличению удельного сопротивления. (Этот процесс характеризуется температурным коэффициентом линейного расширения ).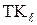

Поэтому температурный коэффициент удельного сопротивления TKr равен их сумме: TKr = TK_R + 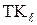. У чистых металлов TKr >> 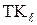, поэтому принимают TKr» TK_R.Однако у сплавов такое недопустимо.

Если удельное сопротивление определить по формуле

r = ,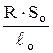

где 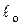– длина проводника при начальной температуре to = 20 °C;

S_о – площадь сечения проводника при начальной температуре to, то будет учтен только температурный коэффициент сопротивления TK_R.

Поэтому при вычислении удельного сопротивления необходимо учитывать также изменение линейных размеров проводника. В лабораторной работе такие измерения не проводятся, поэтому учтем их приближенно. Будем считать, что расширение манганина и нихрома происходит равномерно во всем диапазоне температур с постоянными температурными коэффициентами:

− для манганина TK _ℓ» 1,8×10^-5 1/ ;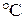

− для нихрома TK _ℓ» 1,6×10^-5 1/ .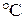

Тогда соответствующее значение удельного сопротивления можно определить по приближенной формуле

r _ℓ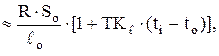

где t_i – температура, при которой вычисляется удельное сопротивление;

t_o – начальная температура (t_o = 20 °C).

Расчетные зависимости r _ℓ = f(t) для манганина и нихрома следует привести на одном графике. Полученные зависимости TK_R = f(t) для манганина и нихрома для сравнения также нужно привести на одном графике.

Дата добавления: 2014-12-27