Усредненное распределение дисперсной фазы по диаметрам для водонефтяных эмульсий 2 страница

1.2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ГРАВИТАЦИОННОГО РАЗДЕЛЕНИЯ ФАЗ [5,8]

1.2.1. Осаждение одиночной сферической
твердой частицы в неподвиж­ной жидкости

На такую частицу будут действовать три силы:

- сила весa (F_G):

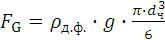; (1.17)

- подъемная сила Архимеда (Fg^’):

(1.18)

- сила сопротивления жидкости равноускоренному оседанию частицы – закон Ньютона (F_A):

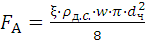(1.19)

где ξ – безразмерный коэффициент сопротивления среды;

w – нарастающая скорость оседания частицы.

Частица оседает под действием разности постоянных сил (Fg) и (F_G'), поэтому она будет двигаться равноускоренно. Но с ростом скорости оседания не­медленно увеличивается сила сопротивления жидкости и в результате после корот­кого участка равноускоренного движения дальнейшее оседание будет происходить с постоянной скоростью (w_ос) под действием следующего баланса сил:

F_G ^_ F_G' = F_A (1.20)

или

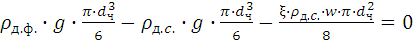, (1.21)

откуда скорость осаждения

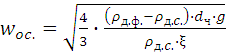. (1.22)

Однако в соответствии с терминологией гидравлики любое движение (в данном случае частицы) происходит либо в ламинарном, либо в турбулентном, ли­бо, наконец, в переходном режимах.

При ламинарном оседании (мелкие частицы или большая вязкость жидкости) сопротивление среды определяется только силами трения.

При турбулентном оседании (крупные частицы или малая вязкость жидко­сти) сопротивление среды определяется образованием турбулентных вихрей.

При переходном оседании сопротивление среды определяется и силами тре­ния и образованием турбулентных вихрей.

Границы между названными режимами определяются численными значе­ниями критерия Рейнольдса:

. (1.23)

Ламинарному режиму соответствует Re <0,2÷2.

Турбулентному режиму соответствует Re≥ 500.

I к переходному режиму соответствует 0,2 ÷2 ≤ Re < 500.

Для нахождения (w_oc) пo уравнению (1.22) необходимо знать (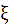), но 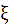= f(Re), т.е. согласно уравнения (1.23) в свою очередь зависит от (w_ос).

Поэтому приходится задаваться режимом осаждения, а после определения (w_oc) проводить проверку, вычисляя Re, т.е. вести расчет методом последователь­ного приближения.

Однозначно решить эту задачу можно, пользуясь критериальным уравнением отстаивания, для вывода которого прежде всего выразим коэффициент сопротивле­ния (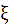) из уравнения (1.24):

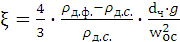. (1.24)

После умножения обоих частей равенства на Re² получим

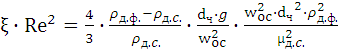(1.25)

или

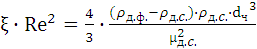. (1.26)

Величина

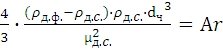(1.27)

носит название критерия Архимеда;в него входят только известные величины.

Тогда

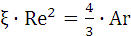(1.28)

или

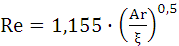. (1.29)

Но если критерий Рейнольдса будет найден, то из уравнения (1.23) легко найти искомую скорость осаждения

. (1.30)

Так вот, при ламинарном режиме (Аr≤36)

(1.31)

Тогда подставим выражение (1.31) в (1.28) и получим

. (1.32)

Подставим это выражение в уравнение (1.30), раскроем критерий Архимеда согласно (1.27) и получим окончательное выражение для скорости осаждения оди­ночной сферической частицы в покоящейся жидкости при ламинарном режиме оса­ждения:

. (1.33)

При турбулентном режиме (Аr≥82500)

. (1.34)

Тогда, подставляя выражение (1.34) в (1.28), получим

. (1.35)

Подставим это выражение в уравнение (1.30), раскроем критерий Архимеда согласно (1.27) и получим окончательное выражение для скорости осаждения оди­ночной сферической частицы в покоящейся жидкости при турбулентном режиме осаждения:

. (1.36)

При переходном режиме (36 < Аг< 82500):

. (1.37)

Критерий Рейнольдса можно вычислить и без знания коэффициента сопро­тивления, если воспользоваться выражением, пригодным для всех режимов осажде­ния:

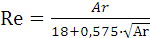. (1.38)

При ламинарном течении вторым слагаемым в знаменателе можно пренеб­речь, и уравнение (1.38) превращается в выражение (1.32).

При турбулентном течении первым слагаемым в знаменателе можно пренеб­речь, и уравнение (1.38) принимает вид

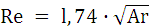. (1.39)

1.2.2. Осаждение несферической одиночной
твёрдой частицы в неподвижной жидкости

Если гравитационному разделению подвергается смесь, содержащая части­цы, форма которых отличается от шарообразных, то скорость их осаждения (w'_oc) рассчитывается по уравнению

w'_oc=φ_ф·w_ос, (1.40)

где φ_ф – так называемый коэффициент формы:

φ_ф=f_ш/f, (1.41)

где f_ш и f – поверхности частиц шарообразной и неправильной формы рав­­ного объёма.

Нахождение знаменателя предполагает знание размеров и формы частицы, а нахождение величины числителя базируется на определении так называемого экви­валентного диаметра частицы:

, (1.42)

где 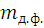– масса частицы неправильной формы;

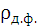– плотность материала частицы неправильной формы.

Поскольку нахождение φ_ф достаточно проблематично, гораздо удобнее воспользоваться его следующими средними значениями для частиц различной формы.

Округлые частицы ……………0,77

Пластинчатые частицы………….0,73

Угловатые частицы………………0,66

Продолговатые частицы…………0,53

Иногда при расчетах используется так называемый фактор несферичности

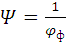. (1.43)

Тогда

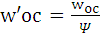. (1.44)

1.2.3. Осаждение одиночной твёрдой частицы
в двигающейся жидкости

Есличастица оседает в двигающейся жидкости, то приходится обращаться к векторной сущности её скорости оседания ()^: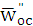

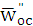= , (1.45)

где 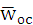– векторная величина скорости оседания частицы (в данном случае сферической и одиночной);

– векторная величина скорости перемещения дисперсионной среды.

1.2.4. Осаждение сообщества одинаковых сферических
твёрдых частиц в неподвижной жидкости

Рассмотренные случаи гравитационного разделения фаз носят название осе­дания и свободных условиях, так как оседающая частица либо одинока, либо их концен­трация настолько мала, что вероятность их взаимодействия при оседании равна ну­лю.

Оседание частиц в среде с их высокой концентрацией, когда их взаимодейст­вие (и прежде всего соударения) становится неизбежным, называется оседанием в стеснённых условиях. Подобные условия реализуются, если φ_ср≥ 5 % об. Причём φ_ср находится как среднее арифметическое между φ_н и φ_к.

В этом случае критерий Рейнольдса можно найти по уравнению

, (1.46)

где ε – относительная доля дисперсионной среды в исходной смеси:

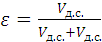, (1.47)

где - объём дисперсионной среды;

– объём дисперсной фазы.

Тогда окончательное выражение для скорости осаждения сферической частицы в неподвижной жидкости в стесненных условиях при любых режимах движе­ния будет иметь вид

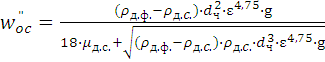. (1.48)

Экспериментальными исследованиями установлена следующая связь между скоростью оседания в свободных и стесненных условиях:

w"_oc = w_oc·εⁿ, (1.49)

где n– эмпирический коэффициент, величину которого в практических рас­четах можно принять равной 4,7.

Известны также зависимости:

w"_oc = w_oc·ε²·10^{-1,82·(1-ε);} (1.50)

. (1.51)

Первая справедлива при ε > 0,7; вторая – при ε< 0,7.

Иногда вместо критерия Архимеда используют критерий Галилея (Ga), взаимосвязь между ними определяется уравнением

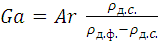, (1.52)

а вместо критерия Рейнольдса используют критерий Лушенко (Ly), взаимо­связь между которыми определяется уравнением

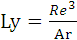. (1.53)

Графически взаимосвязь критериев Рейнольдса, Архимеда и Лушенко проил­люстрирована номограммой на рис.1.2.

10⁰

10²

10³

10⁴

10⁵

10⁶

10⁷

Ar

10^-3

10^-4

10^-2

10^-1

10⁰

10²

10³

10⁴

10⁵

Ly

10⁰

10^-1

10²

10³

10⁴

Re

Рис.1.2. Зависимость критериев Re и Ly от критерия Аr для осаждения
оди­ночной частицы в неподвижной жидкости:

1 и 6 - шарообразные частицы; 2 - округленные: 3 - угловатые;

4 - продолговатые, 5 – пластинчатые

1.2.5. Осаждение полидисперсных твердых частиц
в неподвижной жид­кости

Типичный процесс осаждения частиц из первоначально однородной суспен­зии развивается следующим образом (рис.1.3).

В

В

С

С

D

D

D

A

A

A

a

б

t

h

AB

AC

AD

BC

CD

h_o

h_oo

Рис. 1.3. Типичное развитие процесса периодического осаждения:

а - физическая картина; б - высота поверхности раздела в функции от времени

В начале во всём объёме содержится однородная двухфазная смесь В. При осаждении в верхней части появляется чистая жидкость А, а в основании плотный осадок D. Между областями В и D существует зона С, где концентрация частиц неравномерна. Если частицы имеют почти одинаковые размеры, то между слоями А и В образуется резкая граница, которая перемещается со скоростью оседающих частиц. Между областями В и С может существовать чёткая граница раздела, но может и не существовать.

В конце концов верхняя и нижняя границы раздела сливаются и область В исчезает. После этого происходит медленное сжатие или уплотнение областей С и D по достижении максимальной плотности осевшего слоя.

Математическая теория подобного процесса разработана Кинчем. Согласно его воззрениям процесс отстоя может быть графически описан зависимостью j_fs oт α,

где α – относительная доля дисперсной фазы в исходной смеси:

α= 1-ε, (1.54)

где j_fs – приведённая скорость частиц:

j_fs = v_c·(1-ε), (1.55)

где v_s – средняя скорость движения частиц, в зависимости от условий может быть равна

v_s = w_oc= = (1.56)

Дата добавления: 2014-12-27