
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Гомори
|
|
|
|
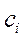
| 
| 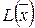
| ||||
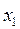
| 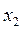
| 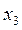
| 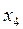
| 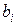
| ||
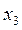
|  1 1
| 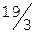
| ||||
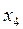
| ||||||
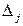
|  -2 -2
| -4 | ||||
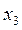
| 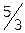
| 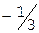
| ||||
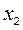
| 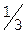
| 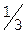
| 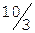
| |||
| 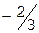
| 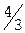
| 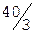
| |||
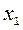
| 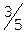
| 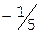
| 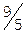
| |||
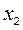
| 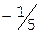
| 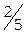
| 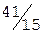
| |||
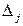
| 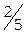
| 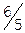
| 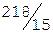
|
Пример. 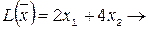 max при ограничениях:
max при ограничениях: 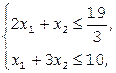
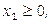
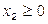 - целые.
- целые.
Решение. 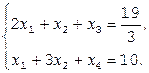
Получим 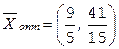 ,
, 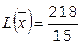 .
.
Найдем дробные части:
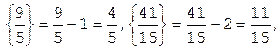
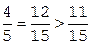 .
.
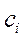
| 
| 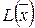
| |||||
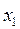
| 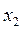
| 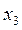
| 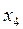
| 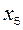
| 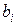
| ||
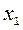
| 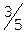
| 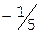
| 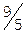
| ||||
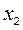
| 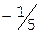
| 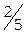
| 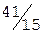
| ||||
| ДОЦ |  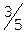
| 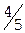
| -1 | 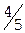
| |||
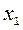
| -1 | ||||||
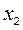
| 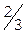
| 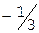
| |||||
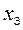
| 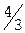
| 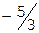
| 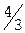
| ||||
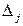
| 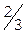
| 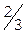
|
Учитывая дробные части чисел 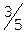 и
и 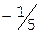 :
: 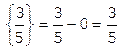 ,
, 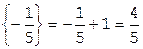 , составляем дополнительное ограничение целочисленности (ДОЦ) для 1-ой строки:
, составляем дополнительное ограничение целочисленности (ДОЦ) для 1-ой строки: 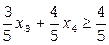 , или
, или 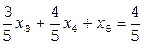 , которые вводим в симплекс-таблицу.
, которые вводим в симплекс-таблицу.
Ответ: 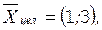
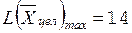 .
.
Задача о назначениях (ЗН).
Задача заключается в выборе такого распределения ресурсов по объектам, при котором минимизируется стоимость назначений.
Возможные применения задачи о назначениях:
| Ресурсы | Объекты | Критерии эффективности |
| рабочие | рабочие места | время |
| грузовые автомобили | маршруты | затраты |
| станки | участки | объем переработанной продукции |
| экипажи | рейсы | время простоя |
| коммивояжер | города | товарооборот |
Матрица стоимостей С имеет вид 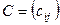 , где
, где 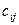 - затраты, связанные с назначением i -го ресурса на j -й объект,
- затраты, связанные с назначением i -го ресурса на j -й объект, 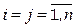 , где n – число объектов или ресурсов.
, где n – число объектов или ресурсов.
Обозначим 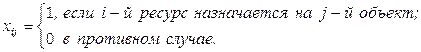
Решение задачи может быть записано в виде 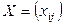 .
.
Допустимое решение называется назначением. Оно строится путем выбора ровно одного элемента в каждой строке матрицы 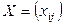 и ровно одно элемента в каждом столбце этой матрицы.
и ровно одно элемента в каждом столбце этой матрицы.
 Элементы
Элементы 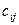 матрицы С, соответствующие элементам
матрицы С, соответствующие элементам 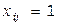 матрицы Х, будем отмечать кружками:
матрицы Х, будем отмечать кружками: 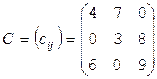
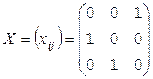 .
.
Математическая постановка задачи о назначениях: 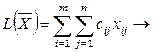 min при ограничениях
min при ограничениях 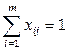 ,
, 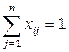 ,
, 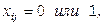
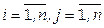 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 521; Нарушение авторских прав?; Мы поможем в написании вашей работы!