
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегральные уравнения. 1 страница
Васин А.В.
Продовження додатка Е
| Марка сталі | S | σод | а | b | c |
| У12А | 1,057 | 70,0 | 0,173 | 0,180 | 3,26 |
| 60С2ХА | 0,946 | 0,139 | 0,115 | 3,84 | |
| ШХ15 | 1,01 | 79,6 | 0,137 | 0,22 | 4,07 |
| В2Ф | 0,95 | 0,135 | 0,119 | 3,99 | |
| 15Х13 | 0,95 | 0,102 | 0,125 | 3,50 | |
| Х18Н10Т | 0,825 | 217,8 | 0,112 | 0,088 | 4,35 |
| 40ХН2МА | 0,966 | 92,7 | 0,125 | 0,175 | 3,4 |
| Х23Н18 | 0,848 | 0,093 | 0,105 | 3,18 | |
| 20Х13 | 0,9 | 0,132 | 0,210 | 3,26 | |
| 15Х25Т | 1,028 | 58,5 | 0,124 | 0,052 | 3,7 |
| 2Х23Н14Г | 0,888 | 0,093 | 0,127 | 3,18 | |
| 4Х8В2 | 0,73 | 0,083 | 0,181 | 3,86 | |
| Х17Н2 | 0,866 | 0,130 | 0,063 | 4,72 | |
| 0Х18МТФ | 0,934 | 56,5 | 0,172 | 0,067 | 3,64 |
| 35Х5МТСФ | 0,947 | 0,127 | 0,103 | 3,99 | |
| 1Х11Н2В2МФ | 0,949 | 0,101 | 0,169 | 3,7 | |
| 30Х2В8Ф | 0,895 | 0,113 | 0,113 | 3,54 | |
| 40ХН2МА | 0,966 | 92,7 | 0,125 | 0,175 | 3,4 |
| 20ХГСНМ | 1,05 | 81,1 | 0,085 | 0,253 | 3,8 |
| 12Х2Н4А | 0,906 | 0,1 | 0,226 | 3,2 | |
| 20Х1М1Ф1ТР | 0,927 | 0,12 | 0,108 | 4,63 | |
| 30Х5МВНФСА | 0,836 | 0,124 | 0,150 | 3,70 | |
| 1Х16Н4Б | 1,023 | 0,106 | 0,139 | 3,95 | |
| 10Х17Н13М2ТГ | 0,906 | 0,072 | 0,173 | 2,31 |
Рекомендовано редакционно-издательским советом Санкт-Петербургского Государственного университета водных коммуникаций
Санкт-Петербург
2011 г.
УДК 517.7
ББК
Рецензенты
Кандидат физико-математических нау доцент Гулевич Н.М.
доктор технических наук, профессор Нырков А.П.
Васин А.В.
Интегральные уравнения: конпект лекций –СПб:СПБГУВК, 2011.-23 стр.
Учебно-методическое пособие содержит основной теоритический материал и конкретные примеры по дисциплине «Интегральные уравнения», и соответствует рабочим программам дисциплины, стандартам, указанной специальности, и может быть использовано при подготовке к экзамену студентами и преподавателями.
Предназначен для студентов четвертого курса (8-ой семестр) специальности 010501.65 «Прикладная математика и информатика».
УДК 517.7
ББК
Васин А.В, 2011
СПБГУВК, 2011
I. Интегральные уравнения Вольтерра
1. Основные понятия
Уравнение

где 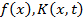 – известные функции,
– известные функции, 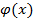 – искомая функция,
– искомая функция, 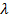 – числовой параметр, называется линейным интегральным уравнением Вольтерра 2-го рода. Функция
– числовой параметр, называется линейным интегральным уравнением Вольтерра 2-го рода. Функция 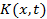 называется ядром уравнения Вольтерра. Если
называется ядром уравнения Вольтерра. Если 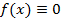 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид
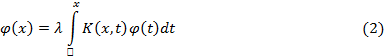
и называется однородным уравнением Вольтерра 2-го рода.
Уравнение
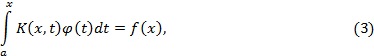
где 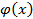 – искомая функция, называют интегральным уравнением Вольтерра 1-го рода. Не нарушая общности, можем считать нижний предел
– искомая функция, называют интегральным уравнением Вольтерра 1-го рода. Не нарушая общности, можем считать нижний предел 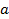 равным нулю, что мы и будем предполагать в дальнейшем.
равным нулю, что мы и будем предполагать в дальнейшем.
Решением интегрального уравнения (1), (2) или (3) называют функцию 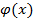 , которая, будучи подставлена в это уравнение, обращает его в тождество (по
, которая, будучи подставлена в это уравнение, обращает его в тождество (по 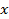 ).
).
2. Связь между линейными дифференциальными уравнениями и интегральными уравнениями Вольтерра
Решение линейного дифференциального уравнения
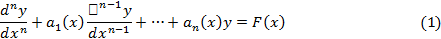
с непрерывными коэффициентами 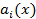 (
(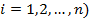 при начальных условиях
при начальных условиях
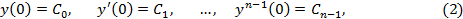
может быть сведено к решению интегрального уравнения Вольтерра 2-го рода.
Покажем это на примере дифференциального уравнения 2-го порядка
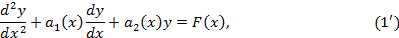

Полагаем

Отсюда, принимая во внимание начальные условия (2’), последовательно находим
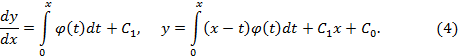
При этом мы использовали формулу
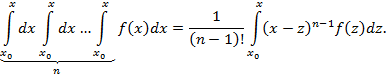
Учитывая (3) и (4), дифференциальное уравнение (1’) запишем так:
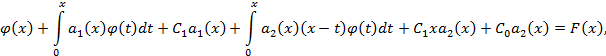
или
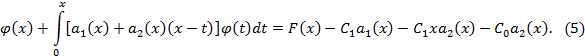
Полагая
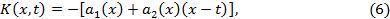
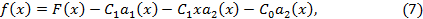
приведем (5) к виду
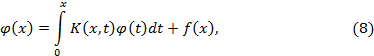
т.е. придем к интегральному уравнению Вольтерра 2-го рода.
Существование единственного решения уравнения (8) следует из существования и единственности решения задачи Коши (1’) - (2’) для линейного дифференциального уравнения с непрерывными коэффициентами в окрестности точки 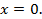
И наоборот, решая интегральное уравнение (8) с 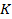 и
и 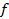 , определенными по формулам (6) и (7), и подставляя выражение, полученное для
, определенными по формулам (6) и (7), и подставляя выражение, полученное для 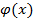 , в последнее из уравнений (4), мы получим единственное решение уравнения (1’), удовлетворяющее начальным условиям (2’).
, в последнее из уравнений (4), мы получим единственное решение уравнения (1’), удовлетворяющее начальным условиям (2’).
Задача 1. Составить интегральное уравнение, соответствующее дифференциальному уравнению

и начальным условиям
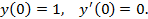
Решение. Полагаем

Тогда
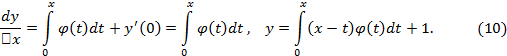
Подставляя (9) и (10) в данное дифференциальное уравнение, найдем

или
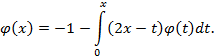
II. Резольвента интегрального уравнения Вольтерра
1. Определение резольвенты
Пусть имеем интегральное уравнение Вольтерра 2-го рода
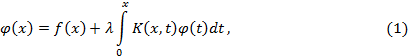
где 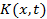 есть непрерывная функция при
есть непрерывная функция при  а
а 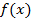 непрерывна при
непрерывна при 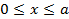 .
.
Будем искать решение интегрального уравнения (1) в виде бесконечного степенного ряда по степеням 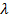 :
:
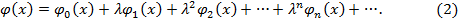
Подставляя формально этот ряд в (1), получим
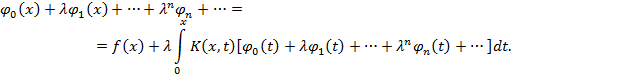
Сравнивая коэффициенты при одинаковых степенях 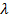 , найдем
, найдем
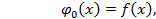

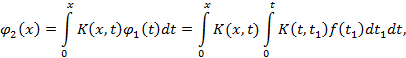
Соотношения (3) дают способ последовательного определения функций  . Можно показать, что при сделанных предположениях относительно
. Можно показать, что при сделанных предположениях относительно 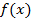 и
и 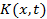 полученный таким образом ряд (2) сходится равномерно по
полученный таким образом ряд (2) сходится равномерно по 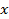 и
и 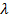 при любом
при любом 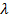 и
и 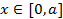 и его сумма есть единственное решение уравнения (1).
и его сумма есть единственное решение уравнения (1).
Далее, из (3) следует:
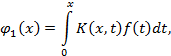
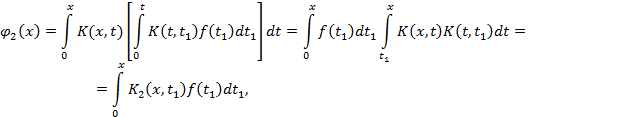
где
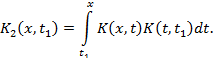
Аналогично устанавливается, что вообще
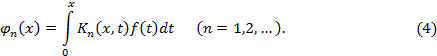
Функции 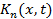 называются повторными или итерированными ядрами. Они, как нетрудно показать, определяются при помощи рекуррентных формул
называются повторными или итерированными ядрами. Они, как нетрудно показать, определяются при помощи рекуррентных формул
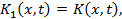

Используя (4) и (5), равенство (2) можно записать так:
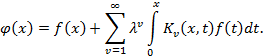
Функция 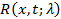 , определяемая при помощи ряда
, определяемая при помощи ряда
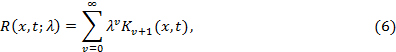
называется резольвентой (или разрешающим ядром) интегрального уравнения (1). Ряд (6) в случае непрерывного ядра 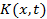 сходится абсолютно равномерно.
сходится абсолютно равномерно.
Повторные ядра, а также резольвента не зависят от нижнего предела в интегральном уравнении.
Резольвента 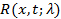 удовлетворяет следующему функциональному уравнению:
удовлетворяет следующему функциональному уравнению:
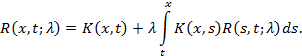
С помощью резольвенты решение интегрального уравнения (1) запишется в виде
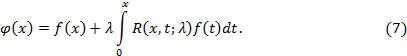
2. Нахождение резольвенты
Задача 2. Найти резольвенту интегрального уравнения Вольтерра с ядром 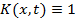 .
.
Решение. Имеем  Далее, согласно формулам (5)
Далее, согласно формулам (5)
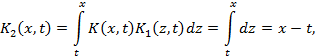
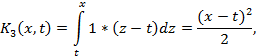
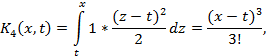
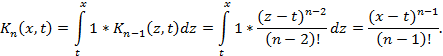
Таким образом, согласно определению
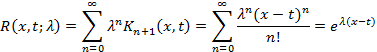
Соотношения (3) дают способ последовательного определения функций 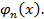 Можно показать, что при сделанных предположениях относительно
Можно показать, что при сделанных предположениях относительно 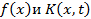 полученный таким образом ряд (2) сходится равномерно по
полученный таким образом ряд (2) сходится равномерно по  при любом
при любом 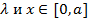 и его сумма есть единственное решение уравнения (1).
и его сумма есть единственное решение уравнения (1).
Далее, из (3) следует:
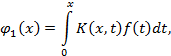
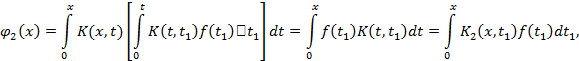
где

Аналогично устанавливается, что вообще
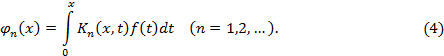
Функции 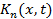 называются повторными или итерированными ядрами. Они, как нетрудно показать, определяются при помощи рекуррентных формул
называются повторными или итерированными ядрами. Они, как нетрудно показать, определяются при помощи рекуррентных формул
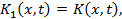

Используя (4) и (5), равенство (2) можно записать так:
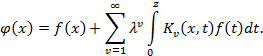
III. Уравнения Фредгольма
1. Основные понятия
Линейным интегральным уравнением Фредгольма 2-го рода называется уравнение вида

где 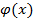 – неизвестная функция,
– неизвестная функция, 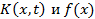 – известные функции,
– известные функции, 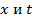 – действительные переменные, изменяющиеся в интервале
– действительные переменные, изменяющиеся в интервале 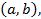
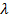 – числовой множитель.
– числовой множитель.
Функция 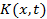 называется ядром интегрального уравнения (1); предполагается, что ядро
называется ядром интегрального уравнения (1); предполагается, что ядро 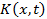 определено в квадрате
определено в квадрате  на плоскости
на плоскости 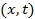 и непрерывно в
и непрерывно в 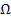 , либо его разрывы таковы, что двойной интеграл
, либо его разрывы таковы, что двойной интеграл

имеет конечное значение.
Если 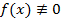 , то уравнение (1) называется неоднородным; если же
, то уравнение (1) называется неоднородным; если же 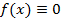 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид
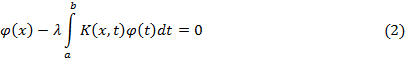
И называется однородным.
Интегральное уравнение вида
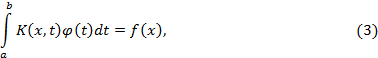
не содержащее искомой функции 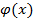 вне интеграла, называется интегральным уравнением Фредгольма 1-го рода.
вне интеграла, называется интегральным уравнением Фредгольма 1-го рода.
Пределы интегрирования 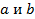 в уравнениях (1), (2) и (3) могут быть как конечными, так и бесконечными.
в уравнениях (1), (2) и (3) могут быть как конечными, так и бесконечными.
Решением интегральных уравнений (1), (2) и (3) называется любая функция 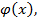 при подстановке которой в уравнения последние обращается в тождества относительно
при подстановке которой в уравнения последние обращается в тождества относительно 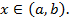
2. Итерированные ядра. Построение резольвенты с помощью итерированных ядер
Пусть имеем интегральное уравнение Фредгольма
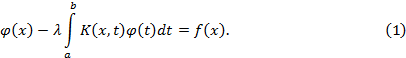
Как и в случае уравнений Вольтерра, интегральное уравнение (1) можно решать методом последовательных приближений. Для этого полагаем
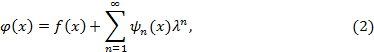
где 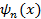 определяются по формулам
определяются по формулам
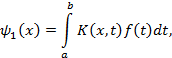
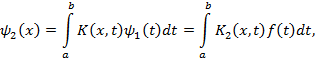
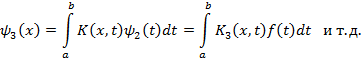
Здесь
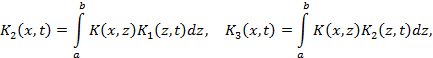
и вообще
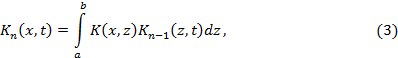
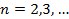 , причем
, причем 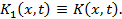 Функции
Функции 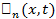 определяемые по формулам (3), называются итерированными ядрами. Для них справедливо соотношение
определяемые по формулам (3), называются итерированными ядрами. Для них справедливо соотношение
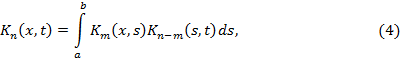
где 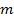 – любое натуральное число, меньшее
– любое натуральное число, меньшее 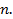
Резольвента интегрального уравнения (1) определяется через итерированные ядра формулой
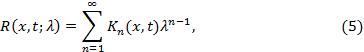
где ряд, стоящий в правой части, называется рядом Неймана ядра 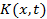 . Он сходится для
. Он сходится для

где
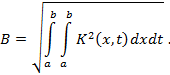
Решение уравнения Фредгольма 2-го рода (1) выражается формулой
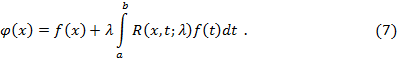
Граница (6) является существенной для сходимости ряда (5). Однако решение уравнения (1) может существовать и для значений 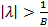 .
.
Пример 1. Найти итерированные ядра для ядра 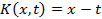 , если
, если 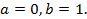
Решение. Пользуясь формулами (3), найдем последовательно:
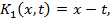
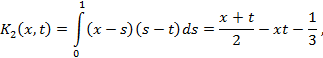

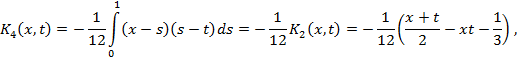
Отсюда следует, что итерированные ядра имеют вид:
1) для n = 2k – 1

2) для n = 2k
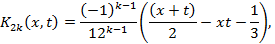
Где k = 1,2,3,…
Пример 2. Найти итерированные ядра 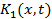 и
и  , если
, если
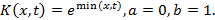
Решение. По определению имеем
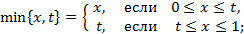
Поэтому данное ядро можно записать в виде
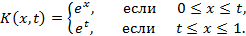
Это ядро, как легко проверить, является симметричным, т.е.
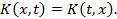
Имеем 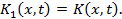 Находим второе итерированное ядро:
Находим второе итерированное ядро:

Здесь

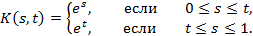
Так как данное ядро 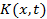 симметрично, то достаточно найти
симметрично, то достаточно найти  только при
только при 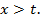
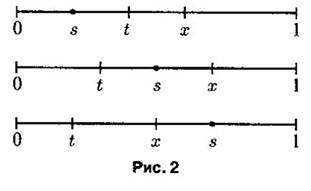
Имеем (рис. 2)
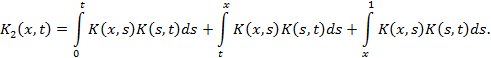
В интервале 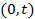 имеем
имеем 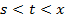 , поэтому
, поэтому
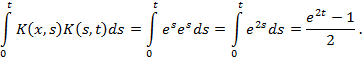
В интервале 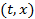 имеем
имеем 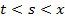 , поэтому
, поэтому
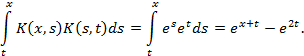
В интервале 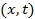 имеем
имеем 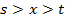 , поэтому
, поэтому
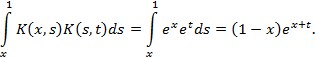
 Складывая найденные интегралы, получим
Складывая найденные интегралы, получим
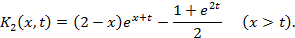
Выражение для  при
при 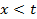 мы найдем, если поменяем местами аргументы
мы найдем, если поменяем местами аргументы 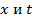 в выражении
в выражении  для
для 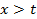 :
:
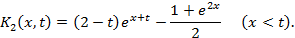
Итак, второе итерированное ядро имеет вид
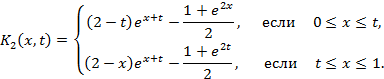
Замечание. Если ядро 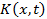 , задаваемое в квадрате
, задаваемое в квадрате 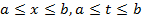 разными аналитическими выражениями, не является симметричным, то следует отдельно рассмотреть случай
разными аналитическими выражениями, не является симметричным, то следует отдельно рассмотреть случай 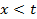 . При
. При 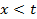 будем иметь (рис. 3)
будем иметь (рис. 3)
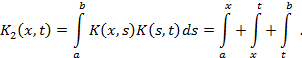
3. Интегральные уравнения с вырожденным ядром
Ядро 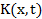 интегрального уравнения Фредгольма 2-го рода называется вырожденным, если оно является суммой конечного числа произведений функций только от
интегрального уравнения Фредгольма 2-го рода называется вырожденным, если оно является суммой конечного числа произведений функций только от 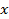 на функции только от
на функции только от  , т.е. если оно имеет вид
, т.е. если оно имеет вид

функции 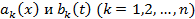 будем считать непрерывными в основном квадрате
будем считать непрерывными в основном квадрате 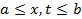 и линейно независимыми между собой. Интегральное уравнение с вырожденным ядром (1)
и линейно независимыми между собой. Интегральное уравнение с вырожденным ядром (1)
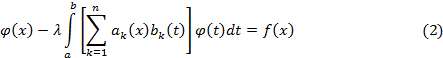
решается следующим образом.
Перепишем (2) в виде

и введем обозначения
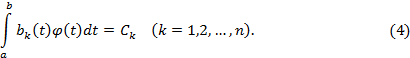
Тогда (3) примет вид
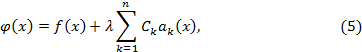
где 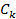 – неизвестная постоянная (так как функция
– неизвестная постоянная (так как функция 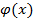 неизвестна).
неизвестна).
Таким образом, решение интегрального уравнения с вырожденным ядром сводится к нахождению постоянных 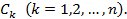 Подставляя выражение (5) в интегральное уравнение (2), после несложных выкладок получим
Подставляя выражение (5) в интегральное уравнение (2), после несложных выкладок получим
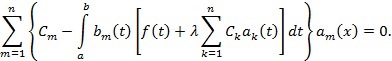
В силу линейной независимости функций 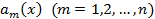 отсюда следует, что
отсюда следует, что

или
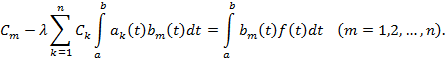
Вводя для краткости записи обозначения
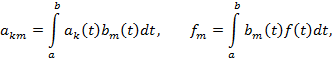
получим, что

или в развернутом виде:
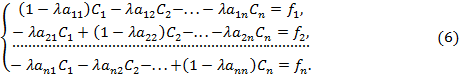
Для нахождения неизвестных 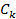 имеем линейную систему из
имеем линейную систему из  алгебраических уравнений с
алгебраических уравнений с  неизвестными. Определитель этой системы равен
неизвестными. Определитель этой системы равен

Если 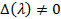 , то система (6) имеет единственное решение
, то система (6) имеет единственное решение 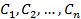 получаемое по формулам Крамера
получаемое по формулам Крамера

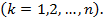
Решением интегрального уравнения (2) будет функция 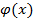 , определенная равенством
, определенная равенством
|
|
Дата добавления: 2014-12-27; Просмотров: 4042; Нарушение авторских прав?; Мы поможем в написании вашей работы!