Пример выполнения работы. Список индивидуальных данных

Список индивидуальных данных

Общая постановка задачи

Теоретическая часть

Лабораторная работа №1. Операции на множествах

Целью лабораторной работы является изучение операций на множествах и приобретение навыков программирования.

Требования к содержанию, оформлению и порядку выполнения

В содержательной части отчета по выполнению лабораторной работы требуется привести описание алгоритмов выполнения операций на множествах, и на основе данных алгоритмов разработать алгоритм для решения задачи согласно своему варианту. Разработанный алгоритм требуется реализовать на языке высокого уровня. Алгоритмы рекомендуется оформлять с помощью блок-схем.

Теоретические сведения, необходимые для выполнения лабораторной работы, представлены в разд.1.1.1-1.1.2

Требуется разработать и реализовать на языке высокого уровня алгоритмы выполнения следующих операций на множествах: объединение, пересечение, разность, симметрическая разность.

Для хранения множеств можно использовать статические целочисленные массивы, т.е допускается, что множества состоят из натуральных чисел и имеют ограниченную константой мощность.

Элементы массива a, используемого для хранения множества A, могут содержать, как сами элементы A, так и формироваться по правилу: a[i]=1, если iÎA; a[i]=0, если iÏA.

В первом случае для хранения множества A={5,2,4} будет использоваться массив a=5,2,4. Во втором случае для хранения того же множества будет использоваться массив a=01011.

Реализацию каждой операции требуется оформить в виде процедуры, входом которой являются два массива, хранящие элементы исходных множеств, а выходом - массив, хранящий элементы множества, полученного в результате выполнения соответствующей операции.

Разработанные процедуры должны использоваться для решения индивидуальной задачи согласно варианту.

Разработайте программу, позволяющую вводить с клавиатуры множества A,B,C и вычисляющую элементы множеств F1 и F2. Элементы множеств F1 и F2 выведите на экран. Выполните тестирование программы на различных входных данных. Обоснуйте полученные результаты.

1. F₁=AI(BUC), F₂=(AIB)U(AIC)

2. F₁=AU(BIC), F₂=(AUB)I(AUC)

3. F₁=(AUB)IA, F₂=A

4. F₁=A\(BUC), F₂=(A\B)I(A\C)

5. F₁=A\(BIC), F₂=(A\B)U(A\C)

6. F₁=A\(A\B), F₂=AIB

7. F₁=A\(AIB), F₂=A\B

8. F₁=AI(B\C), F₂=(AIB)\(AIC)

9. F₁=(A\B)\C, F₂=(A\C)\(B\C)

10. F₁=AU(B\A), F₂=AUB

11. F₁=(AUB)\C, F₂=(A\C)U(B\C)

12. F₁=A\(B\C), F₂=(A\B)U(AIC)

13. F₁=A\(BUC), F₂=(A\B)\C

14. F₁=A∆B, F₂=(A∆B)U(B∆A)

15. F₁=A∆B, F₂=(AUB)\(AIB)

16. F₁=A∆(B∆C), F₂=(A∆B)∆C

17. F₁=AI(B∆C), F₂=(AIB)∆(AIC)

18. F₁=A∆(A∆B), F₂=B

19. F₁=A∆B∆(AIB), F₂=AUB

20. F₁=A∆(AIB), F₂=A\B

21. F₁=(A∆B)U(AIB), F₂=AUB

22. F₁=(A\C)U(B\C), F₂=(AUB)\C

23. F₁=(A\B)U(AIC), F₂=A\(B\C)

24. F₁=(A\B)\C, F₂=A\(BUC)

25. F₁=(A\B)I(A\C), F₂=A\(BUC)

Разработаем программу, позволяющую вводить с клавиатуры множества A,B,C и вычисляющую элементы множества F₁=((AUC)\B)I(A∆C). Элементы множеств F1 выведем на экран. Для множества F₂ требуется выполнить аналогичные действия. Поэтому в данном примере они не рассматриваются.

Для хранения множеств A, B, С будем использовать массивы a, b, c размера mm=10. Также будем считать, что в качестве элементов множеств можно использовать только целые числа от 0 до mm. Массив a формироваться по правилу: a [ i ]=1, если i Î A; a [ i ]=0, если i Ï A. Аналогичным образом формируются массивы B, C.

При таком способе хранения множеств все операции имеют простую реализацию, которая сводится к выполнению логических операций над элементами соответствующих массивов. Если bool mn1[] - массив, хранящий первое множество (первый операнд), а bool mn2[] - массив, хранящий второе множество (второй операнд), то массив bool mn_rez[], хранящий множество, полученное в результате выполнения операции над множествами mn1 и mn2 формируется следующим образом:

• Объединение: for (i=0;i<=mm;i++) mn_rez[i]= mn1[i] || mn2[i];
• Пересечение: for (i=0;i<=mm;i++) mn_rez[i]= mn1[i] && mn2[i];
• Разность: for (i=0;i<=mm;i++) mn_rez[i]= mn1[i] &&!mn2[i];
• Симметрическая разность: for (i=0;i<=mm;i++) mn_rez[i]= mn1[i] &&!mn2[i] || mn2[i] &&!mn1[i];

Все операции реализуем в виде соответствующих функций. Эти функции будем использовать в основной функции для получения требуемого множества F₁=((AUC)\B)I(A∆C). Для этого будем использовать рабочие массивы, т.е. массивы для хранения промежуточных результатов. В данном примере последовательность вычислений может быть следующей: r1=AUC; r2=r1\B; r3=A∆C; r1=r2Ir3=F₁.

Ввод элементов множеств будем осуществлять в консольном режиме. Полностью текст программы приведен ниже.

Для подбора тестовых примеров и наглядного представления результатов рекомендуется нарисовать диаграммы, иллюстрирующие процесс вычисления требуемых множеств. Для рассматриваемого примера данные диаграммы представлены на рис. Л.1.

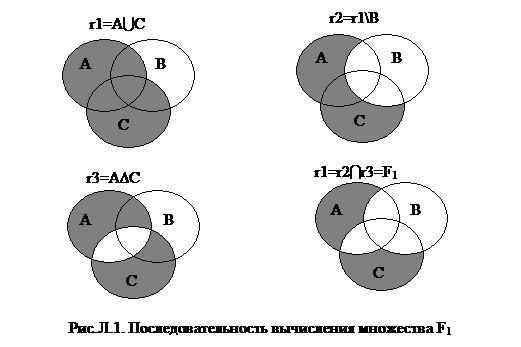#include <stdio.h>

#include <stdlib.h>

#define mm 10 // Максимальное число элементов в множествах

typedef int bool;

// Используемые множества целых чисел от 0 до mm

bool a[mm],b[mm],c[mm], r1[mm],r2[mm],r3[mm];

// Функция print_set(char st [], boolmn [])

// Назначение: Печать элементов множества mn,

// состоящего из целых чисел от 0 до mm-1

// Вход: char st[] - строка сообщения;

// bool mn[] - множество.

// Выход: нет

// Возвращает: нет.

void print_set (char st[], bool mn[]) {

int i;

printf ("%s{",st);

for (i=0;i<mm;i++)

if (mn[i]) printf ("%d ",i);

printf ("}\n");

}

// Функция create_keybrd_set(char st[], bool mn[])

// Назначение: Ввод элементов множества mn с клавиатуры,

// состоящего из целых чисел от 0 до mm-1

// Вход: char st[] - строка сообщения;

// Выход: bool mn[] - множество.

// Возвращает: нет.

void create_keybrd_set (char st[], bool mn[]) {

int i,el;

printf ("Диапазон элементов: %d..%d; число вне диапазона - конец ввода элементов\n",0,mm-1);

printf ("%s",st);

for (i=0;i<mm;i++) mn[i]=0;

scanf ("%d",&el);

while (el>=0 && el<mm)

{mn[el]=1; scanf ("%d",&el);}

}

// Функция unite_sets(bool mn1[],bool mn2[],bool mn_rez[])

// Назначение: Объединение двух множеств,

// состоящих из целых чисел от 0 до mm-1

// Вход: bool mn1[] - первое множество;

// bool mn2[] - второе множество;

// Выход: bool mn_rez[] - объединение множеств mn1 и mn2.

// Возвращает: нет.

void unite_sets (bool mn1[],bool mn2[],bool mn_rez[]) {

int i;

for (i=0;i<mm;i++) mn_rez[i]= mn1[i] || mn2[i];

}

// Функция intersect_sets(bool mn1[],bool mn2[],bool mn_rez[])

// Назначение: Пересечение двух множеств, состоящих из целых чисел от 0 до mm

// Вход: bool mn1[] - первое множество;

// bool mn2[] - второе множество.

// Выход: bool mn_rez[] - пересечение множеств mn1 и mn2.

// Возвращает: нет.

void intersect_sets (bool mn1[],bool mn2[],bool mn_rez[]) {

int i;

for (i=0;i<mm;i++) mn_rez[i]= mn1[i] && mn2[i];

}

// Функция subtract_sets(bool mn1[],bool mn2[],bool mn_rez[])

// Назначение: Разность двух множеств, состоящих из целых чисел от 0 до mm-1

// Вход: bool mn1[] - первое множество;

// bool mn2[] - второе множество.

// Выход: bool mn_rez[] - разность множеств mn1 и mn2.

// Возвращает: нет.

void subtract_sets (bool mn1[],bool mn2[],bool mn_rez[]) {

int i;

for (i=0;i<mm;i++) mn_rez[i]= mn1[i] &&!mn2[i];

}

// Функция s_subtract_sets(bool mn1[],bool mn2[],bool mn_rez[])

// Назначение: Симметрическая разность двух множеств,

//состоящих из целых чисел от 0 до mm-1

// Вход: bool mn1[] - первое множество;

// bool mn2[] - второе множество.

// Выход: bool mn_rez[] - симметрическая разность множеств mn1 и mn2.

// Возвращает: нет.

void s_subtract_sets (bool mn1[],bool mn2[],bool mn_rez[]) {

int i;

for (i=0;i<mm;i++) mn_rez[i]= (mn1[i] &&!mn2[i]) || (mn2[i] &&!mn1[i]);

}

int main (void) {

setbuf (stdout, NULL); // Отменить буферизацию стандартного

// устройство вывода, т.е. консоли.

create_keybrd_set("a=",a);

create_keybrd_set("b=",b);

create_keybrd_set("c=",c);

printf ("Исходные данные:\n");

print_set(" a=",a);

print_set(" b=",b);

print_set(" c=",c);

printf ("Результаты:\n");

unite_sets(a,c,r1);

print_set(" r1=",r1);

subtract_sets(r1,b,r2);

print_set(" r2=",r2);

s_subtract_sets(a,c,r3);

print_set(" r3=",r3);

intersect_sets(r2,r3,r1);

print_set(" f1=",r1);

printf ("Работа программы завершена.\n");

return EXIT_SUCCESS;

}

Для разработки программ в данном лабораторном практикуме используется среда Wascana Eclipse C/C++ IDE for Windows Developers, с которой можно более детально ознакомиться на сайте (http://code.google.com/a/eclipselabs.org/p/wascana/). Рассмотренная программа и результаты ее работы в данной среде представлены на рис.Л2.

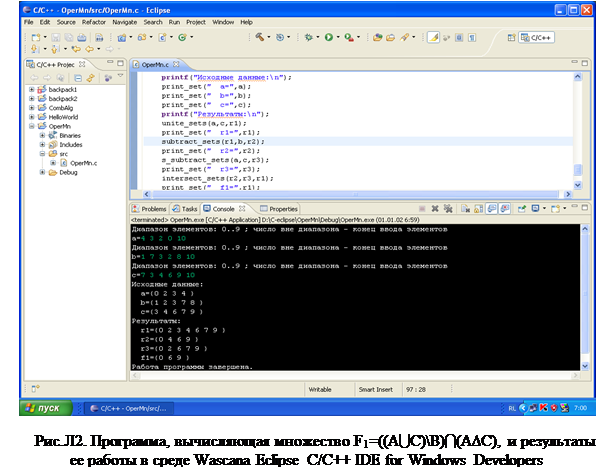
Контрольные вопросы к защите

Список контрольных вопросов совпадает с вопросами для повторения темы 1.

Дата добавления: 2014-12-27