Типы графов

Граф G называется полным, если любые две его вершины смежны.Полный граф порядка n обозначается символом К_n, число ребер в нем равно . На рис. 4.6 изображены графы К_n, n £5.

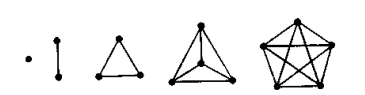Рис. 4.6

Граф называется пустым, если в нем нет ребер. Пустой граф порядка n обозначается через О_n.

Граф, не содержащий вершин и, следовательно, ребер, называется ноль-графом. Граф, состоящий из одной вершины, называется тривиальным.

Красивыми примерами являются графы пяти платоновых тел (т. е. правильных многогранников): тетраэдра, куба, октаэдра, додекаэдра, икосаэдра (рис. 4.7).

Граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из р и из q вершин, обозначается символом K _p,q. При р =1 получаем звезду K_1,q. На рис. 4.8 изображены звезда К_1,5 и полный двудольный граф K_3,3.

Аналогично двудольным графам определяются k-дольный и полный k-дольный графы для k= 3, 4,... На рис. 4.9 приведен трехдольный граф.

Икосаэдр

Октаэдр

Куб

Додекаэдр

Тетраэдр

Рис. 4.7

Рис. 4.8 Рис. 4.9

Легко подсчитать число всех графов с фиксированным множеством вершин X. Эти графы различаются своими ребрами, и потому их число равно количеству подмножеств в X⁽²⁾, т.е. 2 , где п= |X|. Однако эти графы не всегда следует различать. Как в применениях теории графов, так и в самой этой теории чаще существенно лишь то, что есть объекты (вершины графа) и связи между объектами (ребра). С этих позиций графы, которые получаются один из другого изменением наименований вершин, разумно не различать. Оформим эти соображения в виде следующего определения.

Два графа G₁ и G₂ называютсяизоморфными, если существует взаимно-однозначное отображение между множествами их вершин, сохраняющее смежность. Такое отображение называетсяизоморфизмом. Два орграфа изоморфны, если существует изоморфизм между их основаниями, сохраняющий порядок вершин на каждой дуге.

Например, три графа, представленные на рис. 4.10, изоморфны, а графы на рис. 4.11 не изоморф­ны. Вопрос о том, изоморфны ли два данных графа, в общем случае оказывается сложным.

Рис. 4.10

Рис. 4.11

Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы можно отождествлять, т. е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой своих элементов, но именно это игно­рируется при введении понятия «граф».

В некоторых ситуациях все же приходится различать изоморфные графы, и тогда полезно понятие «помеченный граф». Граф порядка п называется помеченным, если его вершинам присвоены некоторые метки, например, номера 1, 2,..., n. Отождествив каждую из вершин графа с ее номером (и, следовательно, множество вершин – с множеством чисел {1, 2,..., n }), определим равенство помеченных графов G₁=(X,V₁) и G₂=(X,V₂) одного и того же порядка: G₁=G₂ тогда, когда V₁=V₂. На рис. 4.12 изо­бражены три разных помеченных графа.

При необходимости подчеркнуть, что рассматриваемые графы различаются лишь с точностью до изоморфизма, говорят: «абстрактный граф». Строго говоря, абстрактный (или непомеченный) граф – это класс изоморфных графов.

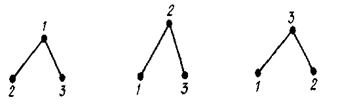
Рис. 4.12

Если вершины графа соединены более чем одним ребром, то такой граф называетсямультиграфом, а ребра – кратными. Мультиграф не допускает петель.

Граф,не содержащий петельи кратных ребер, называется простым.

Граф G=(X,V) называется симметрическим, если в V для любой дуги (x_i, x_j) существует противоположно ориентированная дуга (x_j, х_i). Условимся в этом случае соединять обе вершины одной непрерывной линией без стрелок.

Граф называетсяантисимметрическим, если каждая пара смежных вершин соединена только в одном направлении и петли отсутствуют.

Граф, у которого все вершины имеют одну и ту же степень, называетсярегулярным (однородным) графом. Если степень каждой вершины равна r, то граф называется регулярным (однородным) степени r. На рис. 4.10 изображены регулярные графы степени 3.

Граф, который можно изобразить на плоскости так, чтобы никакие два ребра не пересекались в точках, отличных от вершин, называется планарным графом.

Реберным графом L(G) простого графа G называется граф, вершины которого взаимно однозначно сопоставлены ребрам графа G, причем две вершины в L(G) смежны тогда и только тогда, когда соответствующие им ребра смежны в G.

Орграф G' называется обратным к данному орграфу G, если он имеет те же вершины, что и G, а дуга (x_i, x_j) принадлежит G' тогда и только тогда, когда дуга (x_j, х_i) принадлежит G.

Дата добавления: 2014-12-27