Оценка погрешности расчета

В соответствии с заданием погрешность расчета будет оцениваться методом баланса мощностей. В соответствии с этим методом погрешность расчета определяется по формуле:

,

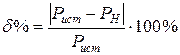где Р _ист – мощность, выделяемая источником,

Р _н – суммарная мощность, потребляемая всеми диссипативными элементами.

Эти мощности определяются по формулам:

,

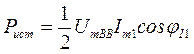где - фаза входного тока .

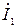Подставляем численные значения в эти формулы, находим значения мощностей:

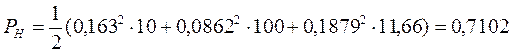Вт

Вт

Подставляем найденные значения мощностей в формулу для определения погрешности:

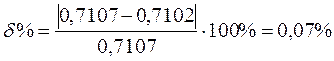
Полученная погрешность удовлетворяет требованию задания.

1.2.2 Расчёт электрической цепи с помощью законов Кирхгофа.

Прежде чем приступить к расчёту названным методом, рассмотрим основные положения этого метода и последовательность расчёта этим методом в соответствии с .

При расчете этим методом первоначально определяются токи в ветвях, а затем напряжения на всех элементах. Токи находятся из уравнений, полученных с помощью законов Кирхгофа. Так как в каждой ветви цепи протекает свой ток, то число исходных уравнений должно равняться числу ветвей цепи. Число ветвей принято обозначать через n. Часть этих уравнений записываются по первому закону Кирхгофа, а часть - по второму закону Кирхгофа. Все полученные уравнения должны быть независимыми. Это значит, чтобы не было таких уравнений, которые могут быть получены путем перестановок членов в уже имеющемся уравнении или путем арифметических действий между исходными уравнениями. При составлении уравнений используются понятия независимых и зависимых узлов и контуров.

Независимым узлом называется узел, в который входит хотя бы одна ветвь, не входящая в другие узлы. Если число узлов обозначим через К, то число независимых узлов равно (К-1).

Независимым контуром называется контур, который отличается от других контуров хотя бы одной ветвью, не входящей в другие контура. В противном случае такой контур называется зависимым.

Если число ветвей цепи равно n, то число независимых контуров равно

[n-(К-1)].

Последовательность расчёта:

1. Расставляем условно – положительные направления токов и напряжений.

2. Определяем число неизвестных токов, которое равно числу ветвей (n).

3. Определяем число независимых узлов и контуров и выбираем их на схеме.

4. С помощью первого закона Кирхгофа составляем (К –1) уравнений для независимых узлов.

5. С помощью второго закона Кирхгофа составляем [ n – (К –1)] уравнений для независимых контуров. При этом напряжения на элементах выражаются через токи, протекающие через них.

6. Решаем составленную систему уравнений и определяем токи в ветвях. При получении отрицательных значений для некоторых токов, необходимо их направления в схеме изменить на противоположные, которые и являются истинными.

7. Определяем падения напряжений на всех элементах схемы.

Для расчёта берём цепь с найденной согласованной нагрузкой и представляем её в комплексной форме (рис. 10).

На схеме имеют место две ветви, содержащие 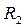и , которые включены параллельно и, как бывает у параллельно соединённых ветвей, у них должны быть общие узлы с обеих сторон соединения. Однако, на схеме каждая ветвь имеет свой узел, между которыми находится перемычка. Такие узлы принято называть распределёнными и на схеме они воспринимаются как один узел. В схеме в этих случаях токи в перемычках не представляют интереса и их не определяют. Исходя из сказанного, в схеме имеется четыре ветви, а значит в схеме четыре неизвестных тока.

С учётом сказанного, в схеме только два узла, а в качестве независимого узла выберем верхний распределённый узел и для него, в дальнейшем будет записано уравнение по первому закону Кирхгофа.

В схеме три независимых контура. Выбираем контура, содержащие такие элементы:

; ; .

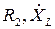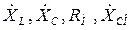Для каждого контура составляются уравнения по второму закону Кирхгофа. Все составленные уравнения образуют следующую систему уравнений 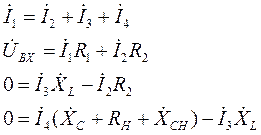(10):

(10)

Расчёт системы можно проводить методом Крамара или методом последовательного исключения. Воспользуемся методом последовательного исключения. Подставим первое уравнение системы во второе уравнение. После эквивалентного преобразования система принимает вид 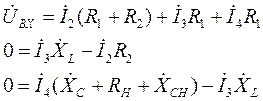(11):

(11)

Из третьего уравнения системы (11) находим ток :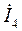

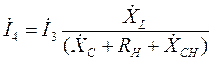. (12)

Подставляем найденный ток (12) в первое уравнение системы (11) и после эквивалентного преобразования система принимает вид (13):

. (13)

Из второго уравнения системы (13) находим ток :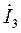

. (14)

Подставляем найденный ток 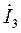(14) в первое уравнение системы (13) и после эквивалентных преобразований, получаем:

.

Решаем полеченное уравнение относительно тока :

.

В полученное выражение подставляем численные значения:

.

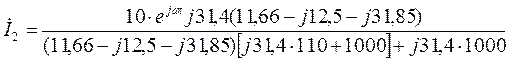Осуществляя необходимые преобразования, получаем решение для в показательной и алгебраической форме:

А. (15)

Ток 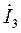находим по формуле (9), подставляя в неё численные значения:

.

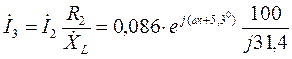После необходимых преобразований находим значение тока 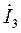в показательной и алгебраической форме:

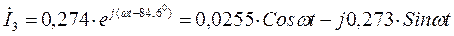А. (16)

Ток 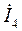находим по формуле (12), подставляя в неё численные значения:

.

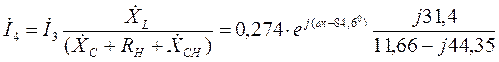После необходимых преобразований находим значение тока 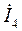в показательной и алгебраической форме:

А. (17)

Ток находим в соответствии с первым законом Кирхгофа по формуле:

Подставляем в это выражение значения токов в алгебраической форме (15), (16), (17) и, суммируя вещественные и мнимые составляющие, находим в начале ток в алгебраической форме, а потом и в показательной:

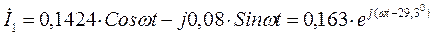А.

Находим напряжения на элементах:

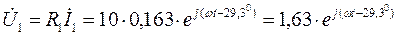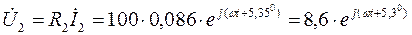В.

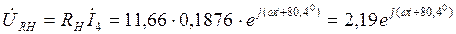В.

В.

В.

В.

Сравнивая полученные здесь результаты расчётов с результатами предыдущего расчёта, видим, что имеет место достаточно хорошее их совпадение.

Определение погрешности расчёта.

Определим мощность, выделяемую источником:

Вт.

Определим мощность, потребляемую диссипативными элементами схемы по известной формуле:

.

Подставляя численные значения найденных токов, находим:

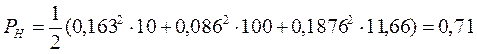Вт.

Погрешность определяем по известной формуле:

.

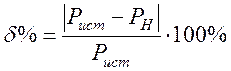Подставляем найденные значения мощностей:

.

Как видим, полученная погрешность удовлетворяет требованию задания.

1.2.3 Расчёт электрической цепи методом контурных токов

Прежде, чем приступить к рассмотрению примера расчёта схемы методом контурных токов, рассмотрим основные положения этого метода и последовательность расчёта в соответствии с .

Сложные схемы характеризуются наличием значительного числа ветвей. В случае применения предыдущего метода это приводит к необходимости решать систему из значительного числа уравнений. Метод контурных токов позволяет уменьшить число исходных уравнений, а значит несколько облегчить расчёт.

При расчёте методом контурных токов используются понятия не зависимого контура и зависимого контура, которые использовались в предыдущем методе. Кроме них в этом методе используются ещё следующие понятия:

- собственный элемент контура - элемент, относящийся только к одному контуру;

- общий элемент контура - элемент, относящийся к двум и более контурам цепи.

Обозначаем, как и раньше, через К число узлов, а через n число ветвей цепи. Тогда число независимых контуров цепи определяется по уже известной формуле [n-(К-1)].

Метод основывается на предположении, что в каждом не зависимом контуре течёт собственный контурный ток, и вначале находят контурные токи в не зависимых контурах. Токи в ветвях цепи определяют через контурные токи. При этом исходят из того, что в собственных элементах контура токи совпадают с контурным током данного контура, а в общих элементах ток равен алгебраической сумме контурных токов тех контуров, к которым принадлежит данный элемент.

Последовательность расчёта:

1. Определяется число ветвей (n) и число узлов (К) цепи. Находится число независимых контуров [n-(К-1)].

2. Выбирается [n-(К-1)] не зависимых контура.

3. Выбирается условно-положительное направление контурных токов в каждом из независимых контуров (обычно показывается стрелкой).

4. Для каждого из независимых контуров составляется уравнение по второму закону Кирхгофа. При этом падение напряжения на собственных элементах определяется как произведение контурного тока на величину сопротивления, а на общих элементах - как произведение алгебраической суммы всех контурных токов, протекающих через данный элемент, на величину его сопротивле-

ния. Обход контура производится, как правило, в направлении собственного контурного тока.

5. Решается система из [n-(К-1)] уравнений и находятся контурные токи.

6. Токи в ветвях схемы находятся следующим образом:

- в собственных элементах контура ток равен контурному току;

- в общих элементах контура ток равен алгебраической сумме токов, протекающих через данный элемент.

Пример применения метода контурных токов при расчёте электрических цепей рассмотрим на той же схеме (рис.6) и представим её на рис.11. Как рассматривалось выше, в этой схеме три независимых контура. Тогда в каждом независимом контуре выбираем направления контурных токов и показываем эти контурные токи.

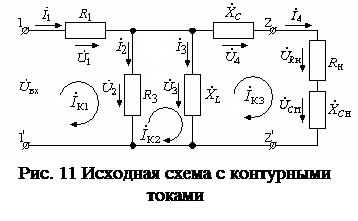Для дальнейшего удобства расчёта расставим в схеме условно-положительные направления токов и напряжений. Далее, в соответствии с п.4 «последовательности расчёта», для каждого независимого контура составляем уравнения по второму закону Кирхгофа. В результате этих действий получаем систему (18) из трёх уравнений:

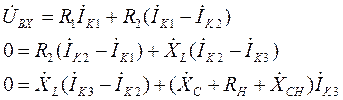(18)

В полученных уравнениях раскрываем скобки и приводим подобные:

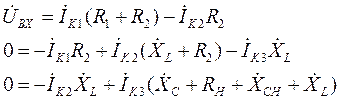(19)

Из третьего уравнения системы (19) находим ток :

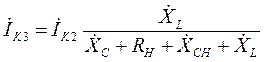(20)

Подставляем выражение тока (20) во второе уравнение системы (19), в результате чего, после приведения подобных членов, эта система принимает вид:

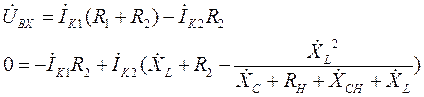(21)

Во втором уравнении системы (21) коэффициент при токе имеет довольно громоздкий вид. Для дальнейшего анализа будет удобно обозначить его какой-нибудь буквой, например 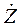, т.к. этот коэффициент имеет размерность сопротивления:

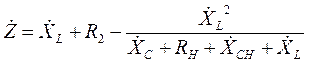. (22)

Подставим численные значения в формулу (22) и найдём значение 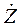в алгебраической и показательной форме:

(23)

С учётом (22) система уравнений (21) принимает вид:

(24)

Из второго уравнения системы (24) найдём ток :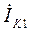

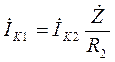. (25)

Подставим выражение для тока 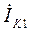(25) в первое уравнение системы (24) и после приведения к общему знаменателю, получим:

. (26)

Из уравнения (26) находим ток :

.

В полученное выражение для тока подставляем численные значения и находим значение тока в алгебраической и показательной форме:

.

Для определения тока 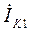воспользуемся формулой (25), подставляем в неё численные значения и находим значение тока в алгебраической и показательной форме:

.

Теперь определяем ток , для чего используем формулу (20). Здесь удобнее будет использовать ток в показательной форме. Подставляем численные значения в (20) и в результате очевидных преобразований получим значение в показательной и алгебраической форме:

.

После определения контурных токов переходим к определению токов в ветвях. В соответствии с методом расчёта токи в собственных ветвях контуров равны контурным токам этих контуров. В соответствии с этим находим токи и :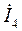

Токи в общих ветвях определяются как алгебраическая сумма контурных токов, протекающих через эти ветви. Ток 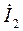равен разности контурных токов 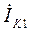и , так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов 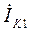и в алгебраической форме и находим значение тока 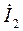в алгебраической и показательной форме:

Ток 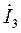равен разности контурных токов и , так как они протекают через эту ветвь в противоположные стороны:

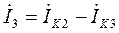
Подставляем численные значения контурных токов и в алгебраической форме и находим значение тока 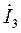в алгебраической и показательной форме:

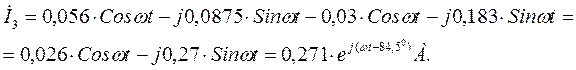
Находим напряжения на элементах:

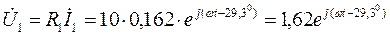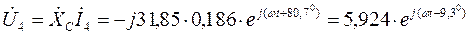В.

В.

В.

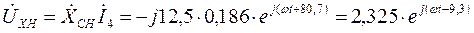В.

В.

Определение погрешности расчёта.

Определим мощность, выделяемую источником:

Вт.

Далее определим мощность, потребляемую диссипативными элементами схемы по известной формуле:

.

Подставляя численные значения найденных токов, находим:

Вт.

Погрешность определяем по известной формуле:

.

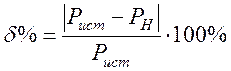Подставляем найденные значения мощностей:

.

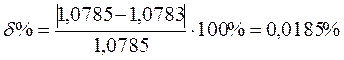Как видим, точность расчёта этим методом выше точности расчёта предыдущих методов и на порядок выше точности расчёта с помощью законов Кирхгофа. Недостатком этого метода является меньшая наглядность по сравнению с другими методами. Воспользоваться рекомендациями приложения 2 в нём можно только после определения всех токов в ветвях.

Наибольшею наглядностью обладает метод эквивалентного преобразования. В нём видно как формируется полное сопротивление цепи, которое определяет входной ток и как этот ток далее распределяется по ветвям.

Дата добавления: 2014-12-27