
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Погрешность
|
|
|
|
Погрешность средств измерений – разность между показанием средства измерений и действительным значением измеряемой физической величины.
Погрешность результата измерений – отклонение результата измерения от действительного значения измеряемой величины. Она в несколько раз больше погрешности средства измерения, которым проводилось измерение, т.к. включает в себя и другие погрешности: методик, условий, оператора при отсчете и записи, математических операций и т.д.
По математическом выражению различают абсолютную, относительную и приведенную погрешность[3].
Абсолютная погрешность СИ выражается в единицах измеряемой величины и равна:
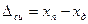 , (1)
, (1)
где xп – показание прибора, xд – действительное значение измеряемой прибором величины.
Абсолютная погрешность результата измерения также выражается в единицах измеряемой величины:
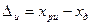 , (2)
, (2)
где xри – результат измерения физической величины.
При грубых однократных измерениях xп и xри могут совпадать. В остальных случаях Δи > Δ, как правило в несколько раз.
Относительная погрешность выражается в процентах и вычисляется по формуле:
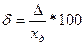 , (3)
, (3)
или по уравнению:
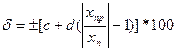 , (4)
, (4)
где c,d – положительные числа, выбираемые из ряда чисел, приведенного для класса точности,
xпр – верхний предел измерения прибора.
Приведенная погрешность также выражается в процентах, используется для сравнения по точности одноименных приборов в том числе с разными пределами измерений и определяется выражением:
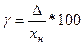 , (5)
, (5)
где xн – нормирующее значение равное верхнему пределу измерения xпр для СИ с нулевой отметкой на краю диапазона измерений.
Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным длине шкалы, соответствующей диапазону измерений. В этом случае приведенную погрешность вычисляют по формуле:
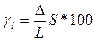 , (6)
, (6)
где 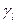 – линейно-приведенная погрешность выраженная в процентах от длины шкалы, %;
– линейно-приведенная погрешность выраженная в процентах от длины шкалы, %;
L – длина шкалы, мм;
S – чувствительность прибора в поверяемой точке шкалы, чувствительность указана в паспорте прибора.
Для экспериментального определения чувствительности в заданной точке диапазона измеряют расстояние 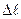 в миллиметрах между двумя соседними отметками шкалы: соответствующей заданной точке и ближайшей к ней. Полученное значение делят на разность показаний
в миллиметрах между двумя соседними отметками шкалы: соответствующей заданной точке и ближайшей к ней. Полученное значение делят на разность показаний 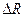 в Омах (т.е. цене деления) соответствующей этим отметкам
в Омах (т.е. цене деления) соответствующей этим отметкам
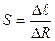 .
.
Пример. Определить чувствительность омметра при показании 30 Ом. Расстояние между соседними отметками 30 и 25 Ом равно 3,7 мм. Чувствительность равна

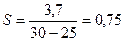 мм/Ом
мм/Ом
Класс точности средств измерений.
Класс точности это обобщенная характеристика средств измерений, определяемая пределами допускаемой основной и дополнительной погрешности, а так же другими свойствами средств измерений, влияющими на точность. Его вводят для удобства условных обозначений пределов допускаемых погрешностей и наносят на средства измерений.
Значения классов точности[4] выбирают из ряда чисел:
| Форма выражения погрешности | Пределы допускаемой основной погрешности, % | Обозначение класса точности на средстве измерений. |
| Относительная по формуле (3) | 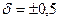
| 
|
| Относительная по формуле (4) | 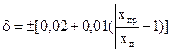
| 0,02/0,01 |
| Приведенная по формуле (5) | 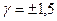
| 1,5 |
| Приведенная по формуле (6) | 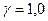
|
 1,0 1,0
|
[1; 1.5; (1.6); 2; 2.5; (3); 4; 5; (6)]*10n (n=1, 0, -1, -2 и т.д.), а примеры их обозначения приведены в таблице 1.
Таблица 1 – обозначения классов точности.
Допустимые значения метрологических характеристик аналоговых амперметров и вольтметров в зависимости от их классов точности приведены в таблице 2.
Таблица 2 – нормируемые величины.
| Нормируемые значения | Допустимые значения нормируемых величин для приборов классов точности, % | |
| 0,5 | 1,5 | |
| Основная погрешность | 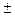 0,5 0,5
| 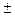 1,5 1,5
|
| Вариация | 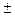 0,5 0,5
| 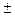 1,5 1,5
|
| Изменение показаний: | ||
- от наклона на 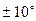
| 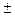 0,5 0,5
| 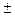 1,5 1,5
|
- от температуры
(для класса 1,5 от 15 до 25 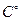 для класса 0,5 от 18 до 20 для класса 0,5 от 18 до 20 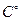 ) )
| 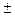 0,3 0,3
| 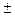 0,8 0,8
|
| - от частоты | 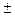 0,5 0,5
| 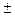 1,5 1,5
|
Основой для присвоенного СИ того или иного класса точности является их основная погрешность и способ его выражения.
Класс точности позволяет рассчитать в каких пределах находится действительное значение измеряемой величины.
Пример: Рассчитать в каких пределах может находится действительное значение измеряемой величины при ее однократном измерении. Измерения проводили вольтметром с верхним пределом измерения 250 В, класс точности обозначен на шкале числом 2,5 без окружности и «галочки» т.е. он установлен по приведенной погрешности. Прибор показал 220 В. Из формулы 5 определяем границы основной допустимой абсолютной погрешности вольтметра
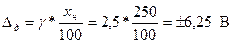 (7)
(7)
Действительное значение напряжения может находится в интервале от
(U - ∆д) до (U + ∆д), где U – показание вольтметра, тогда в нашем примере:
от (220 - 6,25) до (220 + 6,25), т.е. от 213,75 В до 226,25 В, при показании прибора 220 В.
Обращаем внимание, что этот интервал учитывает только основную допустимую погрешность СИ. Если учитывать погрешности от вариации показаний, наклона прибора, изменений частоты в пределах нормальных условий эксплуатации, то интервал может быть увеличен в несколько раз. Поэтому погрешность результата измерения всегда больше погрешности СИ.
Следует заметить, что при нормировании класса точности по приведенной погрешности допустимая погрешность ∆д (7) не зависит от показаний прибора и остается неизменной при любом показании, т.е. если вольтметр покажет 50 В, то ∆д точке 50 то же равно 6,25 В, и интервал будет равен от 43,75 В до 56,25 В. В этом случае относительная погрешность
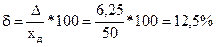
т.е при измерении малых напряжений, находящихся в начале шкалы, относительная погрешность редко увеличивается. В нашем примере она увеличилась с 2,5% в конце шкалы до 12,5% - в пять раз. Поэтому измерять следует в конце шкалы, а для измерении малых сигналов следует использовать приборы с меньшим пределом измерений.
Однако, при нормировании класса точности по относительной погрешности она остается неизменной в любой точке шкалы, а абсолютная погрешность изменяется.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 5150; Нарушение авторских прав?; Мы поможем в написании вашей работы!