Л.П. Чалая, А.И. Конопля

.

.

.

то

.

Задание 3. Исследовать наибольшее и наименьшее значения функции

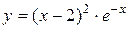
на отрезке [0;3].

Решение. Найдем производную:

.

Отсюда находим критические точки: x ₁=2, x ₂=4. Однако в заданный интервал попадает только одна точка: x ₁=2Î[0;3]. Далее находим значение функции в найденной критической точке и на границах отрезка:

y (2) = 0, y (0) = 4, y (3) = e–3=1/ e ³.

Итак, наибольшее значение рассматриваемая функция принимает на левом конце заданного отрезка: y_наиб = y (0) = 4, а наименьшее значение – в точке минимума: y_наим = y (2) = 0.

Задание 4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:

.

Решение. I. а) Данная функция имеет смысл при всех значениях x, кроме точки x =1, т.е. областью определения данной функции

D = (–¥; 1)È(1;+¥).

Заметим также, что функция может принимать только неотрицательные значения, т.е. y ³0.

б) Данная функция является ни четной, ни нечетной, ни периодической, т.е. это функция общего вида.

в) При x =–1 функция будет равна нулю: y (–1)=0, т.е. график функции пересекает ось Ox в точке A (–1;0). При x =0 функция принимает значение y (0)=1, т.е. график функции пересекает ось Oy в точке B (0; 1).

г) Точка x =1 является точкой разрыва 2-го рода, причем

.

Следовательно, прямая x =1 является вертикальной асимптотой данной функции.

д) Найдем уравнение наклонной асимптоты y=kx+b, где

,

.

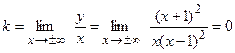Таким образом, рассматриваемая функция имеет горизонтальную асимптоту, уравнение которой y =1.

II. Исследуем функцию на экстремум и определим участки ее монотонности. Для этого вычислим производную:

.

Определим критические точки функции, т.е. точки в которых производная равна нулю или не существует. Это будут точки x ₁=–1, x ₂=1. Наносим эти точки на числовую ось и определяем знак производной на каждом из полученных интервалов: Поскольку при переходе через критическую точку x =–1 производная меняет знак с минуса на плюс, то в этой точке имеется минимум: y(–1)=0. В точке x =1 производная также меняет знак, однако в этой точке нет экстремума, т.к. эта точка является точкой разрыва. На интервалах (–¥; –1) и (1;+¥) функция убывает, на интервале (–1; 1) – возрастает.

III. Исследуем функцию на выпуклость и вогнутость. Для этого вычислим производную второго порядка:

.

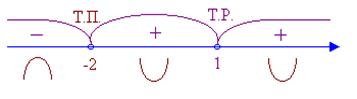Определим критические точки 2-го порядка, т.е. точки в которых вторая производная равна нулю или не существует. Это будут точки x ₁=–2, x ₂=1. Нанесем эти точки на числовую ось и определим знак второй производной на каждом из полученных интервалов. Поскольку при переходе через критическую точку x =–2 вторая производная меняет знак с минуса на плюс, то в этой точке имеется точка перегиба: y(–2)=1/9. На интервале (–¥; –2) функция выпукла, на интервале (–2; +¥) – вогнута.

IV. Строим график функции. Построение начинаем с изображения асимптот, а также наносим точки экстремума, точки перегиба и точки пересечения с осями координат (см. рис.).

Задание 5. Найти все частные производные 1-го порядка:

а) ,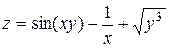

б) ,

в) .

Решение. Частные производные находятся точно также как и обыкновенные производные, только здесь нужно учитывать, что при вычислении производной по одной из переменных все остальные переменные считаются константами.

а) .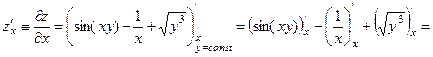

.

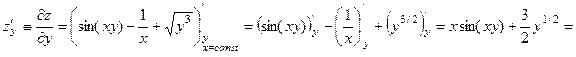
б) .

в) .

Задание 6. Вычислить неопределенные интегралы:

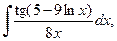
а)	б)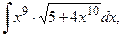
в)	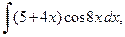г)
д)	е) .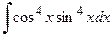

Решение. а) При вычислении данного интеграла, сделаем подстановку t =5–9ln x, в результате получим

.

б) При вычислении данного интеграла, сделаем подстановку t =5+4 x ¹⁰, в результате получим

.

в) При вычислении данного интеграла воспользуемся формулой интегрирования по частям

.

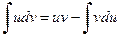Тогда получим

.

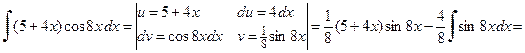
г) При вычислении данного интеграла также воспользуемся формулой интегрирования по частям. В результате получим

.

д) Разложим подынтегральную функцию, т.е. правильную рациональную дробь, на сумму простейших дробей:

.

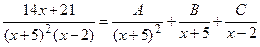Приведем правую часть равенства к общему знаменателю и приравняем числители левой и правой частей:

.

Чтобы найти неопределенные коэффициенты A, B, C, придадим переменной x три каких-либо значения (обычно выбирают такие значения, чтобы получались нулевые значения в правой части):

Таким образом,

.

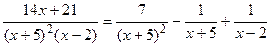Далее, вычисляем исходный интеграл

.

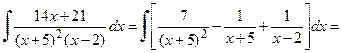
е) Для вычисления исходного интеграла применим тригонометрические формулы:

Тогда получим

.

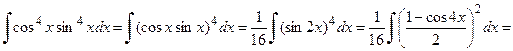
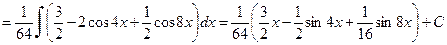Задание 7. Вычислить определенные интегралы:

а)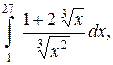

б)

в) .

Решение. а) При вычислении данного интеграла, преобразуем подынтегральное выражение

.

б) При вычислении данного интеграла применим метод замены переменной (обратим внимание, что в определенных интегралах, кроме подынтегрального выражения, преобразуются также и пределы интегрирования):

.

в) При вычислении данного интеграла применим метод интегрирования по частям:

.

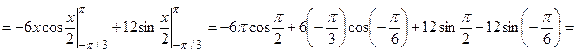
ТАБЛИЦА ПРОИЗВОДНЫХ
ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

1. ,	5. ,
2. ,	6. ,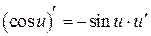
2а. 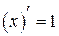,	7. ,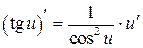
2б. ,	8. ,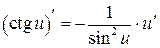
2в. ,	9. ,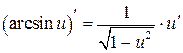
3. ,	9а. ,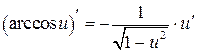
3а. 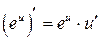,	10. ,
4. ,	10а. .
4а. ,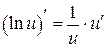

ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

1. 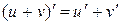,	4. ,
2. 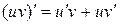,	5. ,
3. 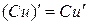,	6. ,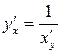

ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ

1. ,	7. ,
2. , a ¹1,	8. ,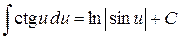
2а. 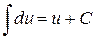,	9. ,
2б. ,	10. ,
2в. ,	11. ,
3. ,	12. ,
4. ,	13. ,
4а. ,	14. ,
5. ,	15. ,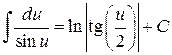
6. 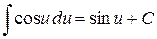,	16. .

Дата добавления: 2014-12-27