Минимальной стоимости. Стоимость единицы площади облицовки дна в

Рассчитать размеры открытого квадратного бассейна – емкости V

восемь раз дешевле стоимости единицы площади стенок. С_ст.1

Ответ выразить в цене С_ст.1

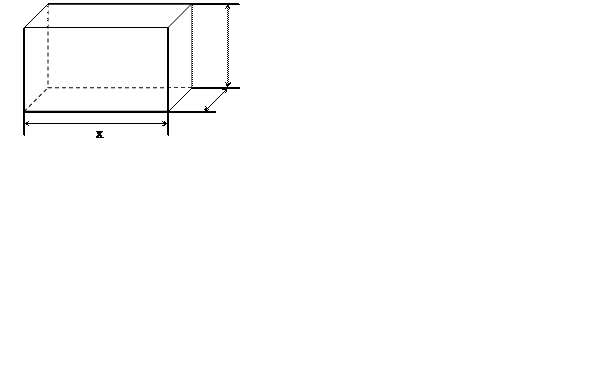Решение.

h=ax;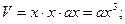

h=ax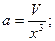

x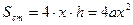

Цена для стен 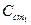, для перекрытия 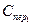, стоимость стен = 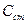₁ 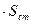, стоимость перекрытия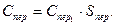

По условию .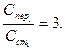

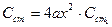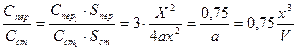
Общие затраты

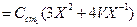
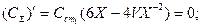
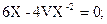
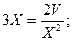
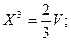
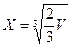
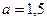
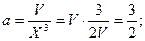
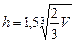
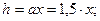
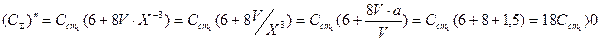(min!)

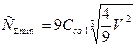
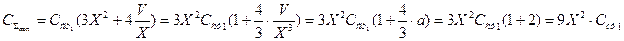
Задача №2/2.

Производится два вида товаров, цены на которые соответственно равныР₁=45 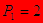и Р₂=26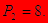

Издержки с учетом корреляционной взаимной связи количества первого вида Х и второго вида Y выражаются функцией С=(X;Y)= 5x² +5XY+3Y² 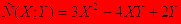Определить при каких количествах X и Y продаж этих товаров прибыль будет максимальной.

Решение.

Прибыль П(X;Y) 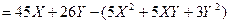Условия локального экстремума (первые частные производные равны нулю) приводят к системе линейных уравнений

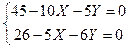- это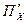

- это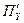

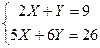
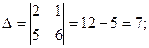
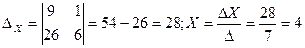
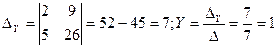
Проверка: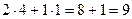

Таким образом

X=4; Y=1

Находим частные производные второго порядка

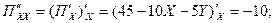
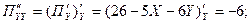
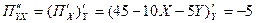
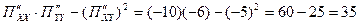>0

Значит, экстремум существует (а не «седло») и это максимум, т.к. 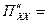-10<0 величина максимальной прибыли при Х=4 и Y=1:

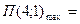
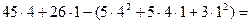103

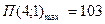
Задача №2/3.

Фирма выпускает два вида товаров. Общие издержки производства с учетом корреляционной взаимной связи с(x;y)= 7x² + 2y – 6xy 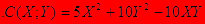, где X и Y – объемы выпуска первого и второго вида товаров соответственно. Общее количество товаров заказано М= Х+Y=45. 100

Сколько нужно выпустить X и Y, чтобы издержки были бы минимальными.

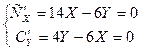Решение

- (1)

- (2)

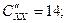
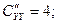
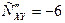
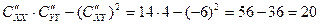>0

Экстремум существует и это минимум, т.к. 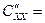14>0.

Из условия экстремума (1):

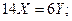
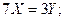
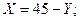
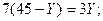
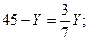
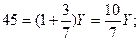
Y = 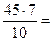31,5; X = 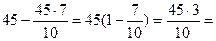13,5

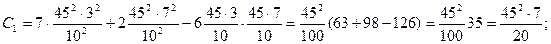
Из условия экстремума (2):

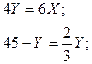
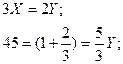
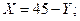
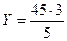
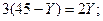
=27

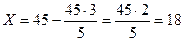
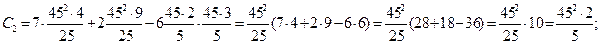
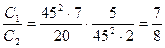<1, т.е. <

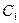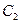
Значит наименьшим из двух минимумов является 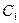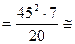708,8.

А действительно:

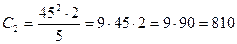>708,8

Задание №3.

Интегральное исчисление.

Задача №3/1

а) Замена переменной.

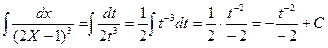
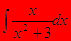
[Примечание: ]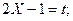

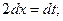
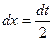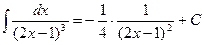
Проверка: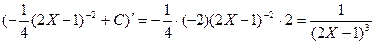

б) Интегрирование дробей, алгебраические преобразования.

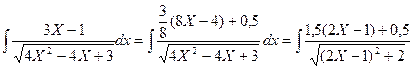
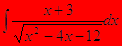
[[Примечание:

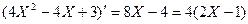
1) Представим числитель в виде, содержащем (8Х-4), т.е.

3Х-1=m(8Х-4)+n и определим значения m и n

3Х-1=8mХ-4m+n; 8m=3;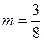

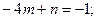
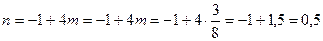
т.о. 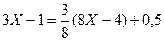и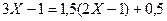

2) Подкоренное выражение тоже представим с содержанием фрагмента (2Х-1)

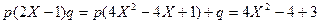
Откуда 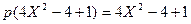и p=1

1+q=3; q =3-1= 2

Значит ]]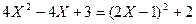

Расчленим данный интеграл на два интеграла

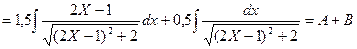и определим отдельно А и В

А)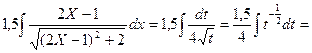

[Примечание: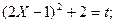

dt=2(2x-1)2dt = 4(2x-1)dx

(2x-1)dx= ]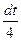

=

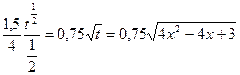
B)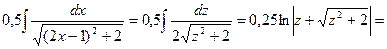

[ ]

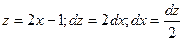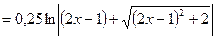
Итого:

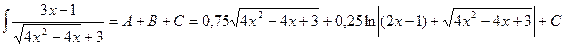
В) интегрирование по частям ∫udv=uv-∫vdu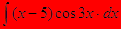

∫(x-5)cos3x∙dx=1/3(x-5)sinx-∫1/3sinx∙dx=[ Примечание:

U=x-5; du=dx; dv=cos3x∙dx; v=∫cos3x∙dx=1/3sinx ]=

=1/3∙ [(x-5) ∙sinx+cosx]+C

Задача №3/2

Дата добавления: 2014-12-27