Формализация вывода средствами логики высказываний

Постановка задачи

Цель кота — не оставить ни одного кусочка сыра, где бы он изначально ни находился. В терминах состояний среды целью кота является перевод ее с помощью своих действий (реакций) в одно из состояний b₇ или b₈. Состояния, в которые с помощью набора допустимых действий необходимо перевести среду, называются целевыми. Процесс определения этих состояний называют формулировкой цели. Будем полагать в рамках нашего примера, что каждое восприятие совпадает с одним из состояний. Задачей агента является нахождение последовательности действий или пар восприятие – действие, ведущих на дереве переходов из начального состояния в целевые. Процесс нахождения этих последовательностей называют поиском, выводом или рассуждением. Постановкой задачи называют задание всех состояний и действий, которые можно использовать для решения задачи, начального состояния и целевых состояний, а также всех допустимых переходов между состояниями при выполнении действий. Для среды кота постановка задачи уже осуществлена. Все состояния, которые могут использоваться при решении задачи, перечислены в табл. 3.1. Целевыми состояниями являются состояния b₇, b₈. Все допустимые переходы между состояниями показаны на рис. 3.2. Из рисунка ясно, что решениями задачи является последовательность b₁/c₂, b₂/c₃,b₄/c₁,b₃/c₃, в результате выполнения которой агент (кот) переведет среду в состояние b₇, и последовательность b₁/c₃, b₅/c₂, b₆/c₃, в результате выполнения которой среда окажется в состоянии b₈.

Для записи задачи на языке исчисления высказываний введем три логические переменные х_к, х_л, х_п.

Истинное значение первой из них означает, что кот находится у левой комнаты, а ложное, что он находится у правой комнаты;

истинное значение переменной х_л означает, что кусочек сыра лежит около левой комнаты, а ложное, что его там нет;

истинное значение переменной х_п означает, что кусочек сыра лежит около правой комнаты, а ложное, что его там нет.

В результате таких обозначений табл. 3.1 можно заменить на табл. 3.2. Каждое состояние среды можно рассматривать как комбинацию (отношение) простейших свойств объектов, задаваемых значениями отдельных логических переменных. Так, состояние b₁ соответствует комбинации свойств кота и кусочков сыра, состоящей в том, что кот находится в левой комнате, и в это же самое время около левой и правой комнат находится по кусочку сыра. На русском языке эту комбинацию можно выразить предложением: «Кот находится около левой комнаты, кусочек сыра лежит около левой комнаты и кусочек сыра лежит у правой комнаты». В соответствии с уже приведенной выше интерпретацией логических переменных х_к, х_л, х_п это предложение можно представить формулой 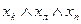, которая истинна в единственном случае - все логические переменные, входящие в нее, истинны, т.е. среда находится в состоянии b₁. Формулы такого типа, являющиеся конъюнкцией переменных с отрицанием или без него, называют элементарными конъюнкциями. Если среда находится в состоянии b₂, то истинна формула и т.д.

Элементарную конъюнкцию, в которую входит по одному разу каждая переменная, определяющую состояние среды, с отрицанием или без отрицания, называют полной конъюнкцией, или конституентой.

Аналогично тому, как были введены логические переменные х_к, х_л, х_п, введем логические переменные z ₁, z₂, z₃ для действий кота “Идти налево”, “Идти направо”, “Съесть “,соответственно. Переменная принимает истинное значение, если выполняется соответствующее ей действие. В противном случае она принимает ложное значение.

		Таблица 3.2
Состояние	Переменные	Формула, описывающая состояние
xk	xл	xп
b1	И	И	И
b2	Л	И	И
b3	И	И	Л
b4	Л	И	Л
b5	И	Л	И
b6	Л	Л	И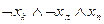
b7	И	Л	Л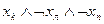
b8	Л	Л	Л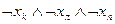

Для простоты будем полагать, что кот не может одновременно выполнять сразу более одного действия.

	Таблица 3.3
Переход	Импликация, соответствующая переходу
Исходное состояние	Действие	Результирующее состояние
b1	c1	b1
b1	c2	b2
b1	c3	b5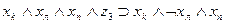
b2	c1	b1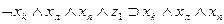
b2	c2	b2
b2	c3	b4
b3	c1	b3
b3	c2	b4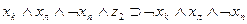
b3	c3	b7
b4	c1	b3
b4	c2	b4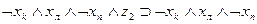
b4	c3	b4
b5	c1	b5
b5	c2	b6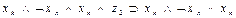
b5	c3	b5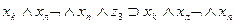
b6	c1	b5
b6	c2	b6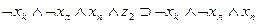
b6	c3	b8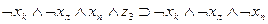

Рассмотрим теперь, как могут быть выражены в виде формул переходы среды из одного состояния в другое при совершении котом того или иного действия. Так, если кот находился в состоянии b₁, и выполнил действие “Идти направо”, то среда перейдет в состояние b₂. Факт нахождения кота в состоянии b₁, и выполнение им в это время действия “Идти направо” означает истинность формулы , а факт перехода состояния b₁ при выполнении действия «идти направо» в состояние b₂ будем интерпретировать как истинность формулы , что позволяет при истинности сделать заключение об истинности 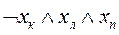. Точно так же можно выразить в виде аналогичных формул все остальные переходы, показанные на рис. 3.2. Представим их в виде табл. 3.3. В первых трех столбцах этой таблицы указаны переходы, имеющиеся на рис. 3.2, а в последнем -формулы, соответствующие переходам.

Дата добавления: 2014-12-27