Сравнение стратегий поиска

Двунаправленный поиск

Идея двунаправленного поиска основана на использовании сразу двух стратегий – прямого поиска от корневой вершины и обратного от целевой вершины. Процесс поиска прекращается, когда оба этих процесса встретятся на середине глубины. Если считать, что степень ветвления при прямом и обратном поиске одинакова, то оценка сложности по времени двунаправленного поиска будет O(2l ^k/2) =O(l^k/2). Эта оценка существенно лучше, чем аналогичная для рассмотренных стратегий поиска. Однако все это в идеале, т.е. при условии, что цель только одна, степень ветвления и сложность нахождения последователей и предшественников одна и та же. При решении практических задач, однако, это условие может нарушаться. Кроме этого могут возникать и другие проблемы. Например, установление факта появления одной и той же вершины в той и другой половине поиска может потребовать значительных усилий и составить значительную долю сложности. Если все эти проблемы можно решить за постоянное время, не зависящее от числа вершин, то оценка сложности по времени двунаправленного поиска останется равной 0(l ^k/2).

Характеристики шести рассмотренных стратегий, где l - степень ветвления, k – глубина поиска, d – максимальная глубина дерева поиска, г – ограничение на глубину поиска, сведены в табл. 4.2.

	Таблица 4.2
Критерии	Поиск
В ши- рину	Монотон- ный в ширину	В глубину	Ограничен- ный в глубину	Итератив- ный в глубину	Двунап- равленный
время	l^k	l^k	l^d	l^r	l^k	l^k/2
память	l^k	l^k	l^d	l^r	l^k	l^k^/2
оптима- льность	да	да	нет	нет	да	да
полнота	да	да	нет	да, если r	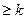да	да

Дата добавления: 2014-12-27