Пример расчета. Задание на выполнение работы

Задание на выполнение работы

Для бетонной колонны, сжатой силой Р, приложенной в заданной точке верхнего сечения, требуется:

1. Выбрать исходные оси и определить моменты инерции сечения относительно этих осей.

2. Определить положение центра тяжести и провести главные центральные оси поперечного сечения.

3. Вычислить главные центральные моменты инерции и радиусы инерции поперечного сечения.

4. Построить ядро сечения.

5. Построить нейтральную ось и определить координаты опасных точек сечения.

6. Определить нормальные напряжения в характерных точках верхнего сечения колонны в долях силы Р.

7. Построить в аксонометрии эпюру нормальных напряжений для верхнего сечения колонны.

8. Подобрать допускаемую величину силы Р с учетом собственного веса колонны.

Форма поперечного сечения колонны и точка приложения силы (рис. 2.6), а также необходимые для расчета данные по табл. 2.1 указываются преподавателем.

Таблица 2.1.

Данные к расчету

Номер варианта	Размер а, м	Высота h, м	Расчетные сопротивления, МПа	Объемный вес ,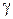
	0,4	3,0	3,5	0,5
	0,6	4,5	5,0	0,6
	0,8	6,0	7,5	0,8
	0,4	4,5	10,0	1,0
	0,6	5,0	14,0	1,3
	0,8	4,5	18,0	1, 6
	1,0	7,0	21,5	1,8
	0,4	4,0	20,0	2,1
	0,6	4,5	35,0	2,5
	1,0	6,5	44,0	2,6
	0,5	4,0	4,0	0,4
	0,7	5,0	6,0	0,7
	0,9	7,0	8,0	0,9
	0,5	6,0	11,0	1,5
	0,7	5,5	15,0	1,7
	0,9	6,5	17,0	1,9
	1,0	8,0	19,0	2,0
	1,1	8,5	18,5	2,1
	1,2	9,0	21,0	2,2
	1,3	9,5	20,5	2,3
	1,4	10,0	22,0	2,44
	1,5	11,0	22,5	2,6
	1,6	12,0	23,0	0,5
	1,7	13,0	24,0	0,6
	1,8	14,0	25,0	0,7
	1,9	15,0	26,0	0,8
	2,0	16,0	27,0	0,9
		17,0	21,5	1,2
	2,2	18,0	20,0	1,4
	2,3	19,0	30,0	1,6

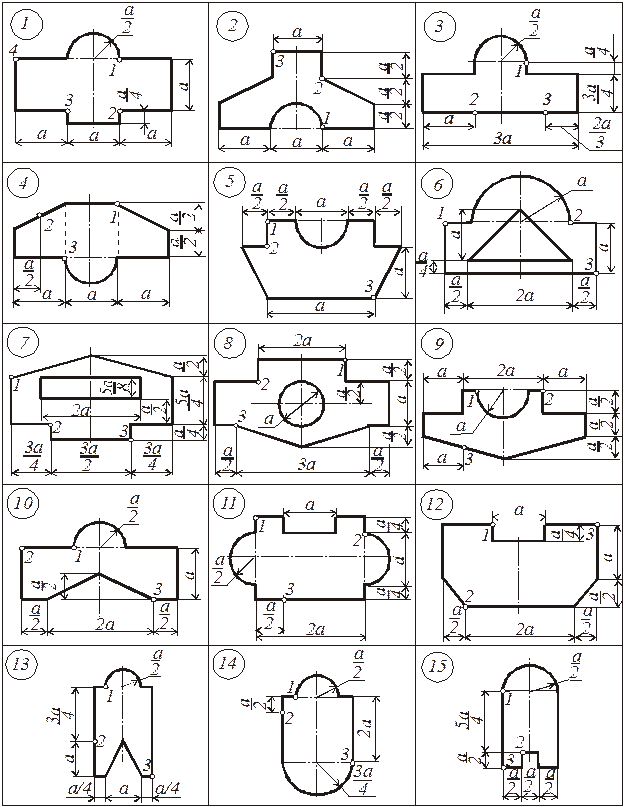
Рис. 2.6. Поперечные сечения колонн

Рис. 2.6. Поперечные сечения колонн (Продолжение)

Оформление работы проводится на листах формата А4 в соответствии с требованиями ЕСКД. На титульном листе указывается название работы, фамилия и инициалы студента, индекс группы, факультет, фамилия и инициалы преподавателя. На первом листе приводится текст задания, схема сечений и исходные числовые данные.

Все расчеты выполняются на втором и последующих листах. Для каждой задачи в масштабе вычерчивается схема сечения, указываются все необходимые размеры сечений и его составных элементов, центральные оси, а также приводятся необходимые формулы с пояснениями, все числовые подстановки и результаты вычислений.

Для бетонной колонны, сжатой силой Р, приложенной в точке 4 верхнего сечения колонны (рис. 2.7), требуется:

Рис. 2.7. Поперечное сечение колонны

- выбрать исходные оси и определить моменты инерции сечения относительно этих осей;

- определить положение центра тяжести и провести главные центральные оси;

- вычислить главные центральные моменты инерции и радиусы инерции поперечного сечения;

- построить ядро сечения;

- построить нейтральную ось и определить координаты опасных точек сечения;

- определить нормальные напряжения в характерных точках верхнего сечения колонны в долях силы Р;

- построить в аксонометрии эпюру нормальных напряжений для верхнего сечения колонны;

- подобрать допускаемую величину силы Р с учетом собственного веса колонны.

Числовые данные: a = 2 м; h = 9 м; = 5 МПа; = 0,6 МПа;

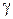= 17 .

Изобразим сечение в масштабе (рис. 2.8).

Рис. 2.8. Простейшие элементы сечения

Выберем исходные оси 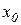, 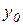. Ось 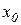проходит через нижние точки сечения, ось 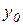совпадает с осью симметрии сечения.

Разбиваем сечение на простейшие части, геометрические характеристики которых определяем по готовым формулам, приведенным в таблице приложения 1:

1) половина круга .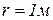

;

;

.

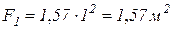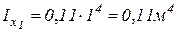2) прямоугольник , .

;

.

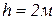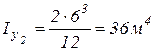3) прямоугольник , .

;

.

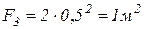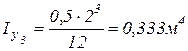Определяем моменты инерции сечения относительно исходных осей , :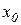

Здесь .

Главная центральная ось y совпадает с осью симметрии и поэтому главный центральный момент

Положение главной центральной оси х определяется по формуле:

,

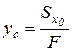где

;

.

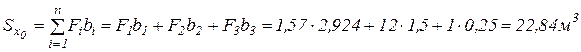Учитывая числовые значения 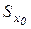и F, получим = = 1,57м. Отложив от оси 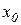, проводим главную центральную ось параллельно исходной оси 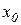. Вычисляем момент инерции относительно этой оси

.

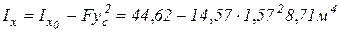Вычисляем радиусы инерции:

; ;

; .

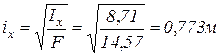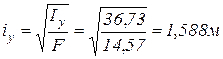Для построения ядра сечения достаточно провести восемь касательных нулевых линий (рис. 2.9).

Рис. 2.9. Ядро сечения и эпюра нормальных напряжений

Отрезки, отсекаемые линиями на осях х и у измеряем на рисунке:

; ; ; ; ; ; ; ;

; ; ; ; ; ; ; .

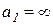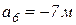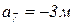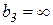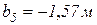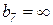Вычисляем координаты полюсов, соответствующих нулевым линиям по формулам (2.6):

; ; ; ; ; ; ; ; ;

; ; ; ; ; ; ; ; .

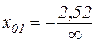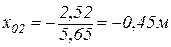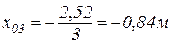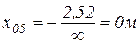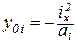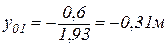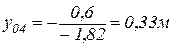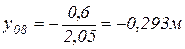По координатам стоим полюсы 1, 2, 3, 4, 5, 6, 7, 8 (рис. 2.9). На участке 2, 3,…, 8 каждая следующая нулевая линия может быть получена в результате вращения предыдущей нулевой линии около фиксированной угловой точки. При этом полюс перемещается по прямой. Поэтому соединим полюсы последовательно прямыми линиями. На участке 8, 1, 2 соединим полюсы плавной кривой. Таким образом ограничиваются контуры ядра сечения.

Сжимающая сила приложена в точке 4. Обозначим ее цифрой 0.

Координаты этой точки: ; .

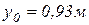Отрезки, отсекаемые нулевой линией на осях х и у соответственно равны

; .

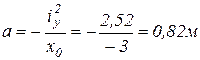Отложим отрезок а на оси х, отрезок b на оси у и проведем нулевую линию n-n (рис. 2.9). Нулевая линия делит сечение на растянутую и сжатую зоны.

Опасными точками сечения являются точки 1 и 0, максимально удаленные от нулевой линии. Напряжения в этих точках найдем по формуле (2.3)

.

В точке 1 с координатами = 3м; 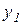= - 1,07м действует наибольшее растягивающее напряжение

.

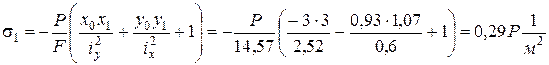В точке 0 с координатами = -3м; 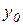= 0,93м действует наибольшее сжимающее напряжение

.

Эпюра нормальных напряжений, значения которых отложены от линии, перпендикулярной к нейтральной оси, показана на рис. 2.9. Каждая ордината этой эпюры определяет величину нормальных напряжений, возникающих в точках поперечного сечения, расположенных на прямой, проходящей через эту ординату параллельно нейтральной оси.

С помощью этой эпюры были найдены напряжения во всех характерных точках сечения (рис. 2.9) и построена в изометрии эпюра нормальных напряжений для верхнего сечения колонны (рис. 2.10).

Подбираем величину нагрузки Р с учетом собственного веса колонны.

Условие прочности по растягивающим напряжениям имеет вид:

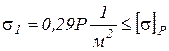, где .

Таким образом

;

откуда Р = 2069 кН.

Условие прочности по сжимающим напряжениям имеет вид:

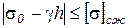, где .

Таким образом

;

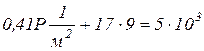откуда Р = 11822 кН.

Из двух значений Р за допускаемое принимаем меньшее:

Р = 2069 кН.

Рис. 2.10. Пространственная эпюра нормальных напряжений

Дата добавления: 2014-12-27