Функции произвольного вида

Найдем нули функции 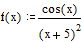на интервале x=[–2,7], используя Mathcad

Изобразим сначала функцию на графике.

На заданном интервале функция три раза обращается в ноль. Определим нули функции, используя встроенную функцию root(f(x),x). Первый аргумент – функция, нуль которой необходимо найти, второй – переменная, которую необходимо варьировать. (Вообще говоря, функция f может быть функцией многих переменных и необходимо указывать, по какой именно переменной мы ищем нуль функции.) Кроме того, необходимо задать начальное приближение поиска. Точность вычислений задается встроенной переменной TOL. По умолчанию ее значение равно 0,001. Это значение можно изменить либо через меню Math/Built–In Variables или непосредственно в тексте документа:

Задаем начальное приближение: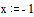

И вычисляем корень: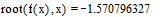

Если требуется найти несколько корней, как в нашей задаче, то имеет смысл определить новую функцию:

Функция r(x) возвращает значение корня ближайшее к x [2], то есть начальное приближение мы задаем через аргумент функции. Задаем вектор начальных приближений x и находим соответствующие им корни X:

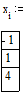
Для данного примера корни легко могут быть найдены аналитически. Они равны на заданном интервале -p/2, p/2 и 3p/2. Полученный численный результат с заданной точностью совпадает с точным решением.

Определение новой функции целесообразно и в том случае, когда мы хотим исследовать зависимость решения от параметра. Пусть функция зависит от параметра a

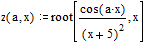
Первый аргумент функции z задает значение параметра, второй – начальное приближение. Найдем корни уравнения при значениях параметра 1 и 2.

Если мы хотим получить комплексный корень, то начальное приближение следует задавать комплексным:

Дата добавления: 2014-12-27