Применение метода Монте-Карло для вычисления кратных интегралов

Вычисление коэффициента корреляции.

Занесем в массив x оценки по высшей математике в сессию в некоторой студенческой группе, а в массив y – оценки по физике. Определим, существует ли какая–либо связь между успеваемостью по физике и высшей математике.

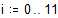
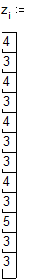
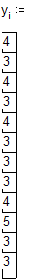
Вычислим средние оценки и стандартное отклонение

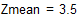
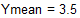
Для вычисления коэффициента корреляции имеется встроенная функция corr

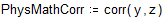
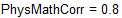
Близкий к 1 коэффициент корреляции свидетельствует о высокой зависимости между успеваемостью по этим предметам.

Хотя Mathcad позволяет вычислять кратные интегралы непосредственно, однако в большинстве случаев при кратности интегралов 3 и более применение метода Монте-Карло предпочтительнее. Дело в том, при одинаковой точности метод Монте-Карло дает существенный выигрыш во времени (в десятки и сотни раз), особенно при большой кратности интегралов. Идея метода состоит в том, что интеграл заменяется величиной Fср.·V, где V – объем области интегрирования, Fср. –среднее значение подынтегральной функции, вычисленное по нескольким случайно выбранным точкам.

Определим подынтегральную функцию.

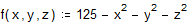
И вычислим интеграл обычным способом (обратите внимание на время счета!)

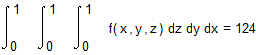
А теперь вычислит тот же интеграл методом Монте-Карло

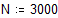
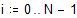
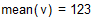
Поскольку в нашем случае объем области интегрирования равен 1, полученное среднее значение совпадает со значением интеграла. При относительной погрешности в 0.001% время вычисления интеграла по методу Монте-Карло существенно меньше.

Интеграл можно вычислить и другим способом. Заключим область интегрирования внутрь прямоугольной области, "набросаем" внутрь полученной области N случайных точек. Тогда интеграл найдем из соотношения 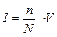,где N – общее число точек, n – число точек, лежащих внутри области интегрирования, V – объем области, включающей область интегрирования.

Максимальное значение подынтегральной функции в области интегрирования не превосходит 125, следовательно, мы может заключить всю область интегрирования внутрь четырехмерного цилиндроида высотой 125 и объемом V=125. Сгенерируем N четверок случайных чисел и подсчитаем, сколько из них лежит под поверхностью f(x,y,z).

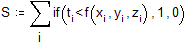
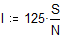
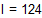
Глава 7. Анализ и синтез сигналов с помощью преобразования Фурье.

Определим функцию, задающую так называемый пилообразный сигнал

и изобразим ее на графике

Заполним массив s: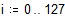

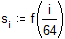
Проводим прямое преобразование Фурье:

Внимание! В том случае, когда в массиве s содержится 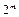элементов, причем все числа действительные, следует использовать функцию fft. Во всех остальных случаях – функцию cfft. Массив g содержит комплексные коэффициенты дискретного преобразования Фурье.

Размер массива f –

Для анализа вклада отдельных гармоник в исходный сигнал изобразим на графике модули и аргументы гармоник

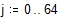
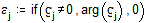
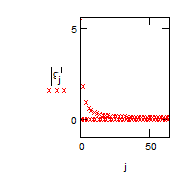
Проводим обратное преобразование Фурье, исключив гармоники с малым вкладом. Будем учитывать только гармоники с амплитудой не менее 0.3. Для отсечения слагаемых с малым вкладом воспользуемся функцией единичного скачка – функцией Хевисайда Ф.

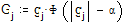
Для обратного преобразования Фурье используется функция ifft, если прямое преобразование осуществлялось с помощью fft, и cifft, если прямое преобразование осуществлялось с помощью cfft.

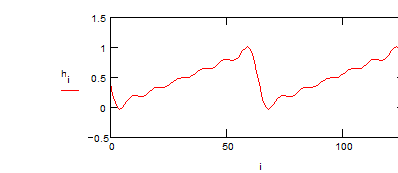
Повторим преобразование Фурье, учтя слагаемые с амплитудой до 0.1.

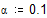
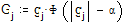
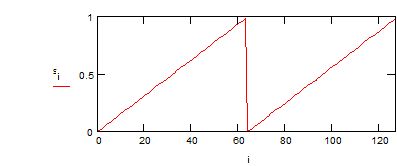
Учет дополнительных гармоник существенно улучшил результат синтеза сигналов.

Литература

1. MATHCAD 6.0 PLUS/ Финансовые, инженерные и научные расчеты в среде Windows 95./ Пер. с англ. – М.: Информационно-издательский дом "Филинъ", 1996. – 712 с.

2. Плис А.И., Сливина Н.А. Mathcad: математический практикум. – М.: Финансы и Статистика. – 1999.

3. Очков В.Ф. Mathcad 8 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1999.

4. Очков В.Ф.. MathCad 7 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1998. – 384 с.

5. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. – М.: CK Пресс, 1997. – 336 с.

6. Дьяконов В.П. Справочник по MathCAD PLUS 7.0 PRO. – М.: CK Пресс, 1998. – 352 c.

7. Дьяконов В. П., Абраменкова И. В. MathCAD 7 в математике, в физике и в Internet. – М.: Нолидж.- 1998. – 352 с.

8. Шелест А. Е. Микрокалькуляторы в физике. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 272 с.

9. Шикин Е.В., Плис А.И. Кривые и поверхности на экране компьютера. Руководство по сплайнам для пользователей. – М.: ДИАЛОГ–МИФИ, 1996. – 240 с.

10. Тейлор Дж. Введение в теорию ошибок. Пер. с англ. – М.: Мир, 1985. – 272 с., ил.

11. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений/ Пер. с англ.; Под ред. А. А. Абрамова. – М.: Наука. Гл. физ.-мат. лит., 1986. – 288 с.

12. Заварыкин В. М., Житомирский В. Г., Лапчик М. П. Численные методы: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов. – М.; Просвещение, 1990. – 176 с.

13. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука. Гл. ред. физ.-мат. лит., 1966.

14. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа. – М.: Наука. Физматгиз, 1962.

Содержание

Введение............................................................................................................................ 3

Глава 1. Нахождение корней уравнений................................................................ 5

Введение..................................................................................................................... 5

1.1. Функции произвольного вида................................................................... 8

1.2. Нахождение корней полиномов............................................................ 10

1.3. Нахождение корней уравнений путем символических преобразований. 10

1.4 Поиск корней уравнений в Mathcad 2000.......................................... 11

Глава 2. Решение систем уравнений и неравенств............................................. 12

ВВЕДЕНИЕ................................................................................................................ 12

2.1. Решение систем линейных и нелинейных уравнений и неравенств. 12

2.2. Решение систем линейных уравнений и неравенств.................. 14

2.3. Символическое решение систем уравнений................................... 14

2.4. Нахождение экстремумов функций.................................................... 15

Глава 3. Аппроксимация функций........................................................................... 18

Введение................................................................................................................... 18

3.1. ЛОКАЛЬНАЯ ИНТЕРПОЛЯЦИЯ................................................................. 18

3.1.1. Линейная интерполяция.......................................................................... 18

3.1.2. Интерполяция сплайнами....................................................................... 19

3.2. ГЛОБАЛЬНАЯ ИНТЕРПОЛЯЦИЯ.............................................................. 24

3.3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.................................................... 27

ВВЕДЕНИЕ............................................................................................................. 27

3.3.1. Аппроксимация линейной функцией.................................................... 27

3.3.2. Аппроксимация полиномами................................................................. 29

3.3.3. Аппроксимация линейной комбинацией функций............................ 31

3.3.4. Аппроксимация функцией произвольного вида................................ 33

Глава 4. Вычисление определенных интегралов................................................ 36

4.1. Метод Ромберга............................................................................................. 36

4.2 Вычисление определенных интегралов.............................................. 38

Глава 5. Решение дифференциальных уравнений.............................................. 40

5.1. Обыкновенные дифференциальные уравнения.............................. 40

Введение................................................................................................................. 40

5.1.1. Метод Эйлера для дифференциальных уравнений первого порядка 42

5.1.2. Решение систем дифференциальных уравнений.............................. 43

5.1.3. Решение дифференциальных уравнений методом Рунге–Кутты 45

5.1.4. Решение дифференциальных уравнений второго порядка........... 46

5.1.5. Решение краевой задачи......................................................................... 47

5.1.6. Решение обыкновенных дифференциальных уравнений в Mathcad 2000 49

5.2. Решение уравнений в частных производных.................................. 51

Введение................................................................................................................. 51

5.2.1. Уравнения гиперболического типа...................................................... 51

5.2.2. Уравнения параболического типа....................................................... 53

5.2.3. Решение уравнений Лапласа и Пуассона........................................... 55

Глава 6. Статистические расчеты на Mathcad.................................................... 58

6.1. Генерация чисел, распределенных равномерно............................. 58

6.2. Генерация случайных чисел, распределенных по нормальному закону. 60

6.3. Вычисление коэффициента корреляции............................................ 63

6.4. Применение метода Монте-Карло для вычисления кратных интегралов 64

Глава 7. Анализ и синтез сигналов с помощью преобразования Фурье...... 66

Литература..................................................................................................................... 68

[1] Получите эти формулы самостоятельно по аналогии с методом Ньютона, оставив в разложении Тейлора первые три слагаемых.

[2] К сожалению, это не всегда так. Если начальное приближение выбрано неудачно и значение производной в этой точке близко к нулю, то, вообще говоря, найденный корень может быть не ближайшим к начальному приближению. В качестве примера решите самостоятельно задачу поиска корня уравнения, выбрав в качестве начального приближения число близкое к. Чем ближе к будет выбранное значение, тем более далекий от 0 корень мы будем получать.

Дата добавления: 2014-12-27