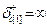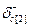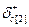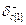Вариациям коэффициентов целевой функции. Анализ чувствительности оптимального решения ЗЛП к

Анализ чувствительности оптимального решения ЗЛП к

		Градиент огр-я 2

Градиент огр-я 3

X[1]

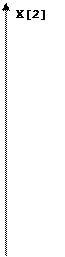Вариации коэффициентов целевой функции ЗЛП приводят к измене­нию направления вектора градиента. Так как при этом не затрагивается допустимое множество, то прежнее решение остается допустимым базис­ным, а оптимальное решение может измениться.

3.1 Графический способ анализа чувствительнос­ти оптимального решения к вариациям C[j].

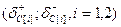На рис. 3.1 приведены результаты графического анализа чувствительности оптимального решения ЗЛП к вариациям коэффициентов целевой функции. Оптимальное решение достигается в крайней точке под номером 4. Определены предельные положительные и отрицательные вариации коэффициентов целевой функции , которые находятся из условия возможности изменения направления 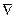Z внутри конуса, определяемого векторами-градиентами активных ограничений 2 и 3.

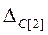При положительной вариации больше предельной оптимальное решение переместится в крайнюю точку(КТ) 3, а при отрицательной - в КТ 5. 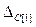Отрицательная вариация больше предельной ( 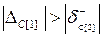) приведет к перемещению оптимального решения либо в КТ 3, либо в КТ 2.

Формальный анализ чувствительности оптимального решения к вариа­циям коэффициентов целевой функции может быть произведен с использова­нием заключительной симплекс-таблицы 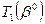. Структура симплекс-таблицы 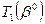для ручного счета имеет следующий вид:

Рис. 3.2 Структура симплекс-таблицы

Вариации коэффициентов целевой функции приводят к изменению симплекс-разностей 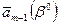. В заключительной симплекс-таблице 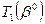все симплекс-разности неположительны. Предельная величина вариации коэффици­ента целевой функции определяется из условия такого изменения симплекс-разностей, при котором одна из них, увеличиваясь, раньше всех станет равной нулю. Тогда дальнейшее изменение указанного коэффициента в том же направлении приведет к тому, что эта симплекс-разность станет положительной и, следовательно, прежнее значение перестанет быть оптимальным.

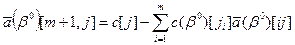Формула расчета симплекс-разности для каждого j-го столбца симплекс-таблицы имеет следующий вид:

(3.1)

где 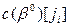-коэффициенты целевой функции при базисных переменных;

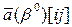-коэффициенты матрицы 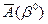, являющейся составной частью симплекс-таблицы .

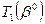Анализ этой формулы позволяет выделить два случая:

- варьируется ;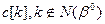

- варьируется ,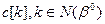

где 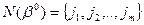- базисное множество, соответствующее оптималь­ному решению

В первом случае 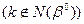будет меняться лишь симплекс-разность k-о столбца

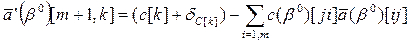(3.2)

К изменению оптимального решения при этом может привести лишь положительная вариация 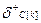, которую можно определить, приравняв соотношение (3.2) к нулю:

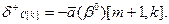(3.3)

Предельные отрицательные вариации по коэффициентам целевой функции небазисных переменных равны:

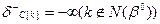(3.4)

Рассмотрим второй случай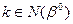

Пусть 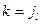. Тогда:

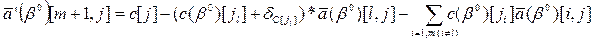(3.5)

Очевидно, что при вариациях такого 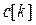будет изменяться не одна симплекс-разность, а все те из них, которым в l-ой строке матрицы 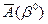соответствуют ненулевые коэффициенты.

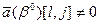(3.6)

При этом увеличиваться симплекс-разности будут в следующих случаях:

- при положительных вариациях 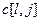, если ;

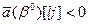- при отрицательных вариациях 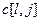, наоборот, если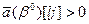

В соответствий с этими рассуждениями формулы для определения предельных вариаций коэффициентов целевой функции для случая 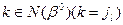имеют вид:

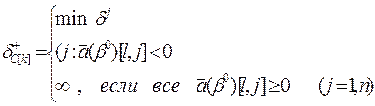
(3.7)

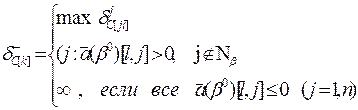(3.8)

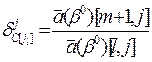
Дата добавления: 2014-12-27