
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. 1). Задача на определение ускорения
|
|
|
|
1). Задача на определение ускорения.
Уравнение движения тела имеет вид х = 15t + 0,4 t2 м. Найти ускорение движения тела.
Решение.
Воспользуемся определением ускорения
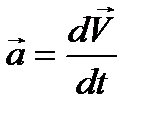

По условию задачи движение является прямолинейным вдоль оси х, поэтому для определения ускорения необходимо взять дважды производную от функции
х = 15t + 0,4 t2 по времени.
 ,
,
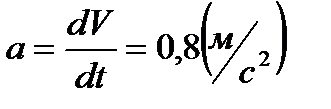 .
.
Ответ: 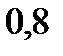
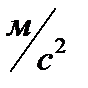
2). Задача на равноускоренное движение.
При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определить перемещение тела за седьмую секунду?
| Решение Проведем ось Х в направлении движения тела, а оси выберем в точке, из которой тело начинает движение. Тогда х4 – перемещение тела за 4 секунды, |
| СИ 0,9 м |
Дано:
S5 = 90 см
| S7 =? |
х5 – перемещение тела за 5 секунд, причем, согласно уравнению равноускоренного движения,
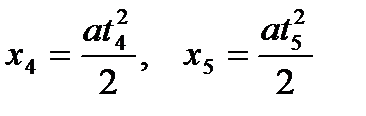 ,
,
где t4 = 4 c, t5 = 5 c. Следовательно, перемещение тела за пятую секунду равно
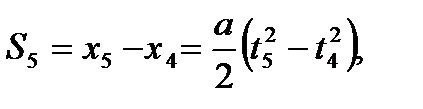
откуда
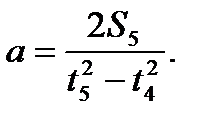 (1)
(1)
Аналогично, перемещение тела за седьмую секунду равно
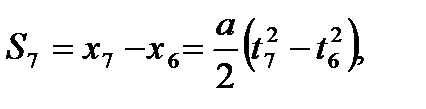
где х6, х7 – перемещение тела за 6 и 7 секунд соответственно, а t6 = 6 c, t7 = 7 c.
С учетом уравнения (1) получим расчетную формулу:
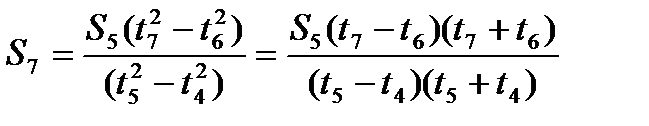 .
.
Проведем проверку размерности:
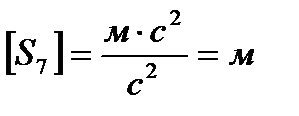 .
.
Теперь можно провести вычисления:
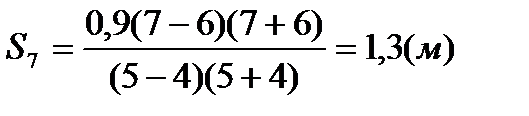

Ответ: 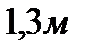
3). Задача на движение тела в поле тяжести Земли, брошенного под углом к горизонту.
Мяч брошен со скоростью 10 м/с под углом 300 к горизонту. Найти высоту его наибольшего подъема.
Запишем краткое условие задачи.
| Решение: В данной задаче все величины приведены в системе СИ. Для ее решения воспользуемся формулой |
V0 = 10 м/с
α = 300
| h =? |
y = 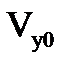 ·t -
·t - 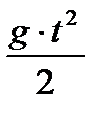 ,где
,где 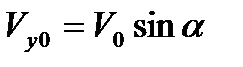 . В точке наивысшего подъема вертикальная составляющая скорости равна 0, т.е. Vy =
. В точке наивысшего подъема вертикальная составляющая скорости равна 0, т.е. Vy = 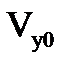 - g·t = 0. Из этого условия определим время подъема мяча:
- g·t = 0. Из этого условия определим время подъема мяча:
t = 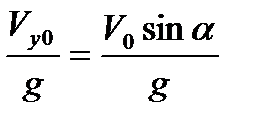 .
.
Тогда высота наибольшего подъема
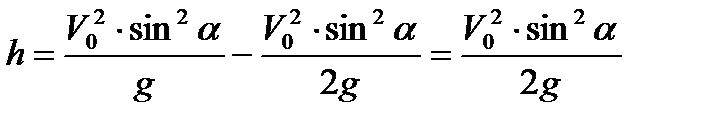 .
.
Проведем проверку размерности:
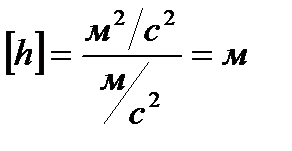 .
.
Вычислим высоту наибольшего подъема:
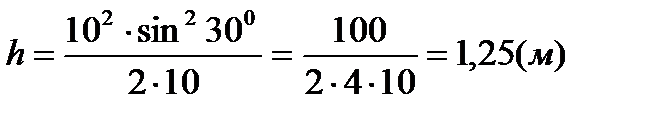 .
.
Ответ:1,25м.
4). Задача на движение связанных тел.
Невесомый блок укреплен на конце стола. Гири одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири о стол μ = 0,1. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением в блоке пренебречь.
Дано: Решение.
m1 = m2 = 1 кг Выполним рисунок, на котором μ = 0,1 укажем все силы, действующие Найти: а на тела, и направление ускорения
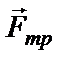
|
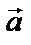
|
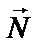
|
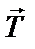
|
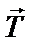
|
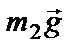
|
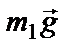
|
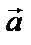
|
Запишем уравнения II закона Ньютона для 1 и 2 тела в векторной форме, объединив уравнения в систему:
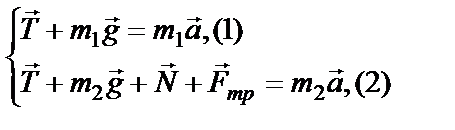
Выберем систему координат XOY и запишем уравнения (1) и (2) в проекции на оси OX и OY.
OX: T – Fтр = m2a (3)
OY: N – m2g = 0 (4)
T – m1g = − m1a (5)
Сила трения скольжения прямо пропорциональна силе нормального давления:
Fтр = μN.
Из уравнения (4) N = m2g, тогда преобразуем уравнение (3):
T – μm2g = m2a
Учтем, что m1 = m2 = m, и получим
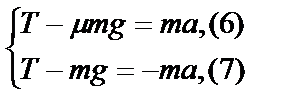
Решая эту систему, получим выражение для ускорения:
−μmg + mg = ma + ma
mg(1 – μ) = 2ma
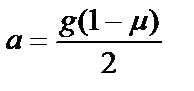 (8)
(8)
Вычислим ускорение:
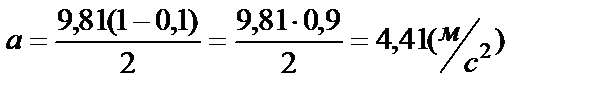
Выразим силу натяжения нити из уравнения (6):
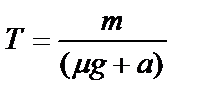 и вычислим ее
и вычислим ее
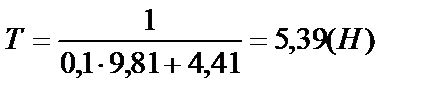 .
.
Вывод размерности: 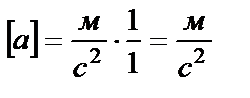 ;
;
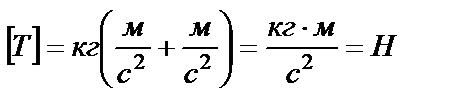 .
.
Ответ: а = 4,41 м/с2; Т = 5,39 Н.
5). Задача на движение связанных тел.
К одному концу нити, перекинутой через блок, подвешивают груз массой 500 г, к другому груз массой 300 г. Найти ускорение системы и, перемещение каждого груза через 1,2 с после начала движения. Трение не учитывать, массами блока и нити пренебречь.
| Решение: Выполним чертеж к задаче, обозначив на нем все силы, приложенные к грузам. |
| СИ 0,5 кг 0,3 кг |
Дано:
m1 = 500 г
m2 = 300 г
t =1,2с
| a =? S =? |
Составим уравнения движения для каждого груза в отдельности. Учтем, что нить нерастяжима, поэтому | 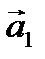 |=| |=| 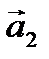 | = a. Введем ось Y, направленную вертикально вверх. Запишем по II закону Ньютона уравнение движения 1-го тела | = a. Введем ось Y, направленную вертикально вверх. Запишем по II закону Ньютона уравнение движения 1-го тела
|
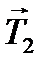
|
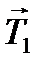
|
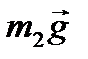
|
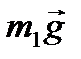
|
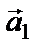
|
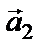
|
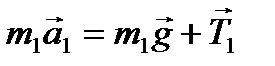
и спроецируем его на ось Y:
-m1a =- m1g +T1.
Составим уравнение движения для 2-го тела
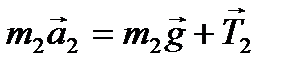
и его проекцию на ось Y:
m2a = - m2g +T2.
Так как блок невесомый | 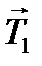 | = |
| = |  | =T.
| =T.
Тогда решим полученную систему двух алгебраических уравнений с двумя неизвестными:
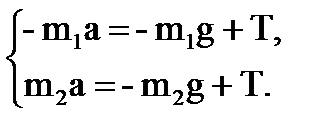
Вычтем из второго уравнения первое:
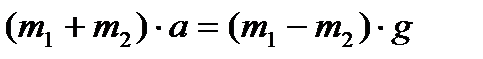 .
.
Отсюда найдем а:
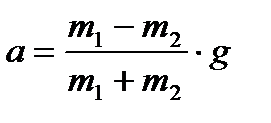 .
.
Для нахождения перемещения грузов (оно одинаково для обоих грузов) воспользуемся формулой для равноускоренного движения с нулевой начальной скоростью:
S = 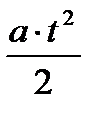 .
.
Проведем проверку размерности:
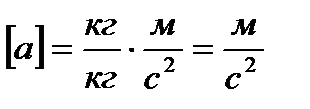 ,
,
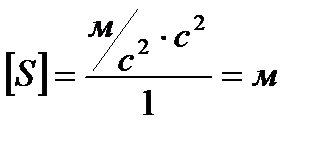 .
.
Перейдем к вычислениям:
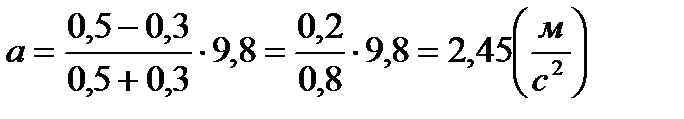 ,
,
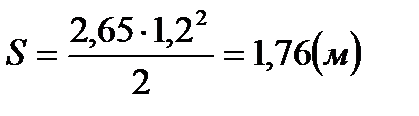 .
.
Ответ: 2,45 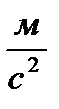 ; 1,76 м.
; 1,76 м.
6). Задача на динамику криволинейного движения.
Определить скорость движения автомобиля массой 2 т по вогнутому мосту радиусом 100 м, если он давит на середину моста с силой 2,5·104 Н.
| Решение: Выполним чертеж к задаче, обозначив на нем все силы, приложенные к автомобилю. Под действием этих сил автомобиль приобретает центростремительное |
| СИ 2·103 кг |
Дано:
m=2 т
R =100 м
P = 2,5·104Н
ускорение, направленное в сторону вогнутости моста. Составим уравнение движения автомобиля
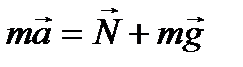
|
| V =? |
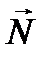
|
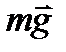
|
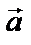
|
Спроецируем это уравнение на ось OY:
ma=N-mg
и учтем, что центростремительное ускорение связано со скоростью движения автомобиля формулой:
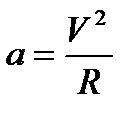 ,
,
а сила нормальной реакции со стороны моста по III закону Ньютона равна по модулю силе давления автомобиля на мост, т.е.
N = P
Получим формулу:
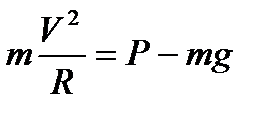 .
.
Откуда:
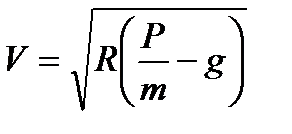 .
.
Проведем проверку размерности:
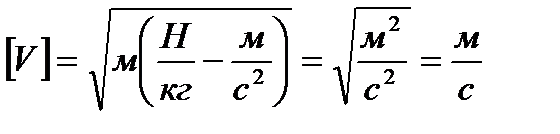 ,
,
Перейдем к вычислениям:
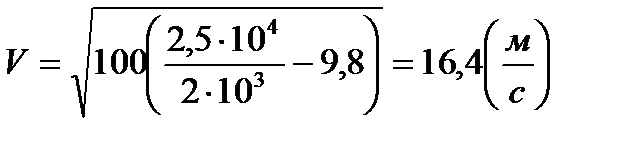
Ответ: 16,4 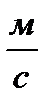 .
.
7). Задача на закон сохранения импульса.
Какую скорость получит неподвижная лодка, имеющая вместе с грузом массу 200 кг, если находящийся в ней пассажир выстрелит в горизонтальном направлении? Масса пули 10 г, ее скорость 800 м/с.
| СИ 1·10-2 кг |
| Решение: Рассмотрим механическую систему лодка-пуля. В начальный момент времени система покоилась и импульс системы Р 0 =0. Так как в системе не действуют внешние |
m л = 200 кг
V л0 =0 м/с
m п = 10г
V п = 800м/с
| V лк =? |
силы, импульс системы не изменяется, т.е. Р 0 =Р к =0. Конечный импульс системы складывается из импульса пули и импульса лодки после выстрела:
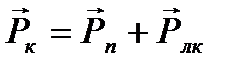 =0.
=0.
Введем ось ОХ, направленную вдоль движения пули и составим проекцию полученного векторного уравнения на эту ось:
Р п -Р лк =0.
Отсюда Р лк = Р п = m п ·V п.
Так как Р лк = m л ·  V лк,найдем скорость лодки после выстрела
V лк,найдем скорость лодки после выстрела

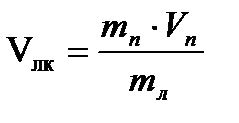 .
.
Проверка размерности в данной задаче очевидна.
Перейдем к вычислениям:
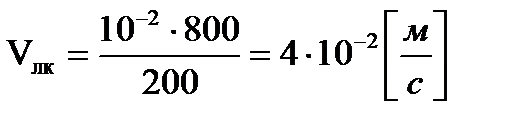
Ответ: 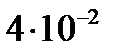
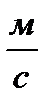 .
.
8). Задача на закон изменения энергии.
Камень, скользящий по горизонтальной поверхности льда, останавливается, пройдя расстояние 48 м. Определить начальную скорость камня, если известно, что коэффициент трения равен 0,06.
Запишем краткое условие задачи.
| Решение: Для решения задачи применим закон изменения механической энергии. Так как камень скользит по горизонтальной поверхности льда, его потенциальная энергия не изменяется. Начальная |
S = 48 м
f = 0,06
| V 0 =? |
кинетическая энергия камня равна 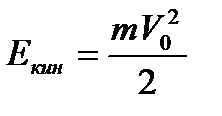 .
.
Конечная кинетическая энергия камня равна 0. Изменение кинетической энергии равно работе силы трения. Таким образом:
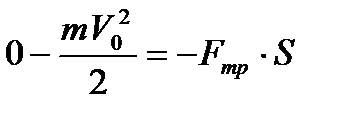 ,
,
Сила трения по закону Кулона равна
F тр = f·N,
где N = mg – сила нормальной реакции поверхности льда. Следовательно
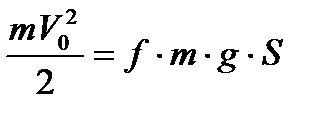 .
.
Отсюда найдем начальную скорость:
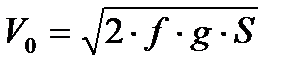 .
.
Проверка размерности:
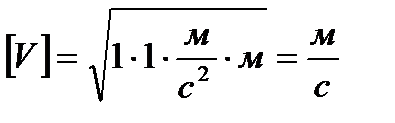 .
.
Проведем вычисления:
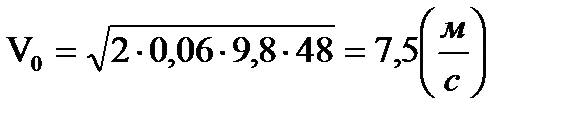
Ответ: 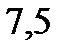
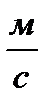 .
.
9) Задача на вращательное движение.
Диск массой m = 2 кг катится без скольжения по горизонтальной плоскости со скоростью v = 4 м/с. Найти кинетическую энергию диска.
| m = 2 кг v = 4 м/с |
| Найти: Wкин - |
поступательного и вращательного движения:
Wк=Wпост + Wвращ (1)
При поступательном движении кинетическая энергия тела 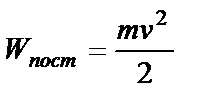 . (2)
. (2)
При вращательном движении 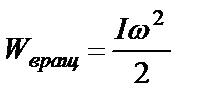 , (3)
, (3)
где 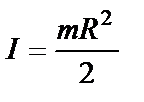 (4) – момент инерции диска,
(4) – момент инерции диска,
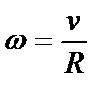 (5) – угловая скорость вращения.
(5) – угловая скорость вращения.
Подставим выражения (4) и (5) в (3), получим
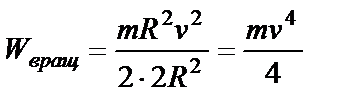 (6).
(6).
Подставив формулы (6) и (2) в (1), окончательно получим:
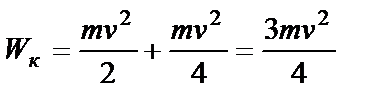 .
.
Вычислим искомую величину:
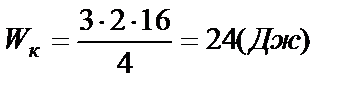 .
.
Вывод размерности:
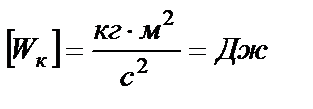 .
.
Ответ: Wк = 24 Дж.
10). Задача на колебания.
Точка совершает гармонические колебания согласно уравнению x = 0,4 sinπt (м). Определить скорость и ускорение точки через 1/6 c от начала колебаний.
| Дано: |
| Найти: v -? a -? |
| x = 0,4 sin πt (м) t = 1/6 с |
Запишем уравнение гармонических колебаний в общем виде:
x = A sin ωt, (1)
где x – смещение точки;
А – амплитуда; ω – круговая частота; t – время.
По определению, скорость равна производной от смещения по времени:
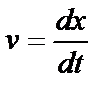 . (2)
. (2)
Подставив (1) в (2), продифференцируем полученное выражение:
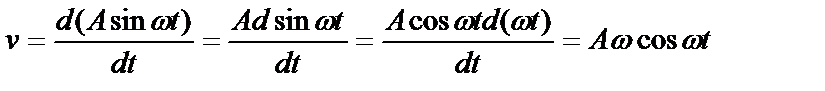 . (3)
. (3)
По определению, ускорение равно производной от скорости по времени:
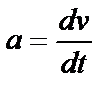 . (4)
. (4)
Подставив (3) в (4), продифференцируем полученное выражение:
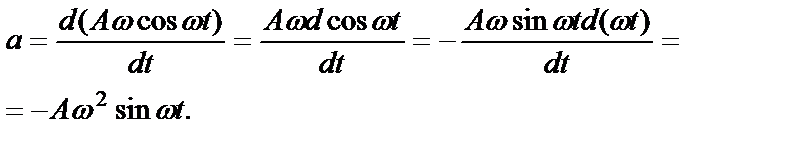 (5)
(5)
Из сравнения уравнения x = 0,1 sin πt и формулы (1) видно, что А = 0,1 м, ω = π с-1. По формулам (3) и (5) вычислим скорость и ускорение:
v = 0,1π cos πt, a = 0,1π2 sin πt. (6)
Проверим формулы (6), подставив единицы измерения:
[v] = м∙с-1 = м/с, [a] = м∙(с-1)2 = м/с2.
Вычислим искомые скорость и ускорение точки:
v = 0,4∙3,14 cos(π/6) = 1,091 м/с,
а = − 0,4∙3,142 sin (π/6) = −1,971 м/c2.
Ответ: v = 1,088 м/с, а = −1,971 м/c2.
11). Задача на явления переноса.
Определить, при каком градиенте плотности углекислого газа через каждый квадратный метр поверхности почвы продиффундирует в атмосферу в течение 1 ч масса газа m = 720 мг, если коэффициент диффузии D = 0,04 см2/с.
Найти: 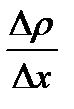 -? -?
|
| S = 1м2 t = 1час m = 720 мг D = 0,04 cм2/с |
| 3,6∙103 с 7,2∙10-4 кг 4∙10-6 м2/с |
Решение: Масса газа, переносимая в результате диффузии, определяется законом Фика: 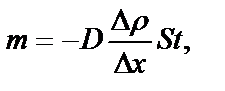 (1) (1)
|
где D – коэффициент диффузии; 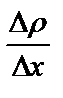 – градиент плотности, т.е. изменение плотности, приходящееся на 1 м толщины слоя почвы; t – длительность диффузии.
– градиент плотности, т.е. изменение плотности, приходящееся на 1 м толщины слоя почвы; t – длительность диффузии.
Из (1) выразим искомый градиент плотности:
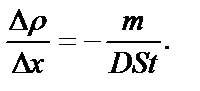 (2)
(2)
Проверим формулу (2), подставив единицы измерения
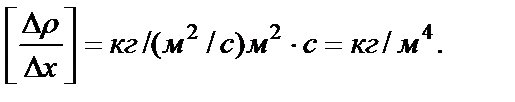
Вычислим градиент плотности:
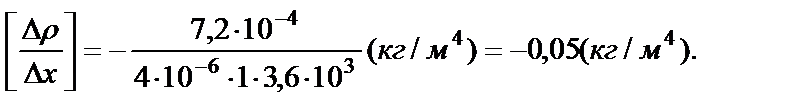
Отрицательное значение градиента плотности соответствует тому, что диффузия происходит в направлении убывания плотности вещества.
Ответ: 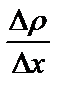 = − 0,05 кг/м4.
= − 0,05 кг/м4.
12). Задача на I начало термодинамики.
Водород массой m = 200 г расширяется изобарически под давлением p = 3∙105 Па, поглощая в процессе расширения теплоту Q = 20 кДж. Определить работу расширения газа.
| Найти: A -? |
| m = 200 г p = 3∙105 Па Q = 20 кДж i = 5 |
| 0,2 кг 2∙104 Дж |
Работа, совершаемая газом при неизменном давлении, выражается формулой
А = p(V2-V1) (1) Из уравнения Менделеева-Клапейрона, записанного
для начального и конечного состояний газа (рV1=mRT1/μ, pV2=mRT2/μ) выразим неизвестные начальный V1 и конечный V2 объемы
V1= mRT1/(pμ); (2)
V2= mRT2/(pμ). (3)
Подставив (2) и (3) в (1), получим
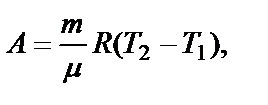 (4)
(4)
где μ – молярная масса водорода, R = 8,31 Дж/(К∙моль) – молярная газовая постоянная; Т1 и Т2 – начальная и конечная температуры газа.
Из формулы для теплоты при изобарическом процессе
Q = mcp(T2 − T1),
где ср – удельная теплоемкость газа при постоянном давлении, выразим неизвестную разность температур:
Т2 − Т1 = Q/(mcp). (5)
Известно, что
ср = (i + 2) R/(2μ), (6)
где i – число степеней свободы молекулы газа. Подставив (6) в (5), а затем результат в (4), получим
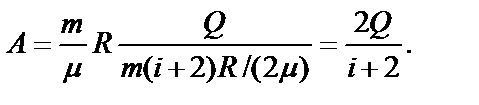 (7)
(7)
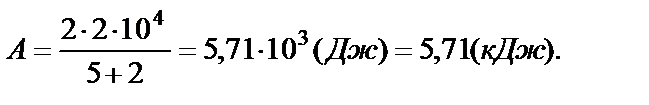
Вывод размерности: из формулы (7) имеем
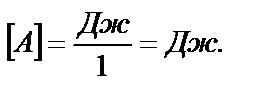
Ответ: А = 5,71∙103 Дж.
13). Задача на применение I закона термодинамики.
Воздух массой 100г, температура которого 270С, нагревается при постоянном давлении и его объем увеличивается в 2 раза. Найти количество теплоты, которое пошло на нагревание воздуха, работу газа при расширении, приращение внутренней энергии.
Запишем краткое условие задачи.
Решение:
Количество теплоты сообщенное воздуху: 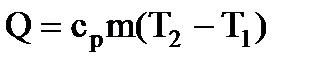 , ,
|
Дано: СИ
m=100г =0,1кг
t1=270C T1=300К
V2=2V1
Q, A, ΔU-?
где сp=103Дж/(кг·К)- удельная теплоемкость воздуха при постоянном давлении (из справочной таблицы). По закону Гей – Люссака 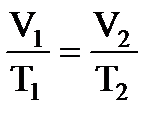 , отсюда
, отсюда 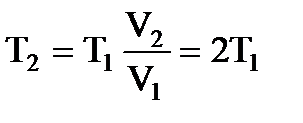 . Работа газа при изобарическом процессе равна:
. Работа газа при изобарическом процессе равна: 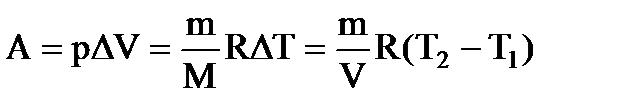 . Приращение внутренней энергии по I закону термодинамики:
. Приращение внутренней энергии по I закону термодинамики: 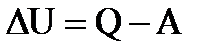 .
.
Проведем проверку размерности:
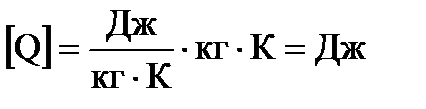 .
.
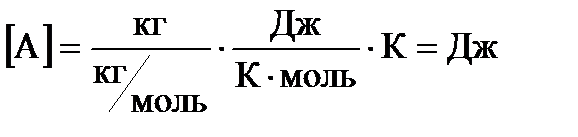 .
.
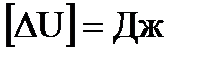
Молярная масса воздуха: M=29·10-3кг/моль.
Произведем вычисления:
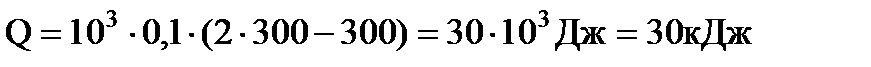 ,
, 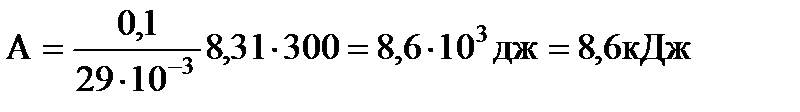 ,
, 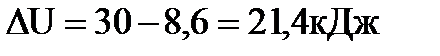
Ответ: 30 кДж, 8,6кДж, 21,4кДж.
14). Задача на КПД тепловой машины.
Температура нагревателя и холодильника идеальной тепловой машины соответственно равны 1170С и 270С. Количество теплоты, получаемое от нагревателя за 1 с, равно 60 кДж. Найдите КПД машины, количество теплоты, отдаваемое холодильнику в 1с, и мощность машины.
Запишем краткое условие задачи
Решение:
КПД тепловой машины: 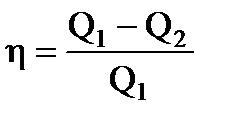 .КПД идеальной тепловой .КПД идеальной тепловой
|
Дано: СИ
t1=1170С T1=390K
t2=270С T2=300K
Q1=60кДж =60·103Дж
t=1c
Q2? N-?
машины 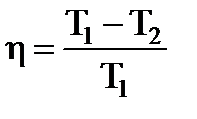 . Приравниваем правые части:
. Приравниваем правые части: 

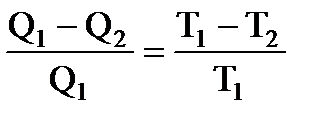
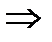
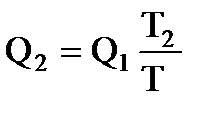 .
.
Мощность тепловой машины 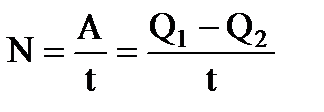 .
.
Произведем вычисления: 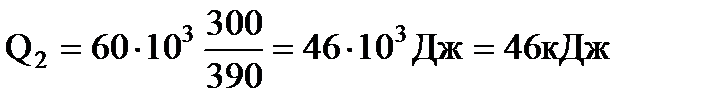 ,
, 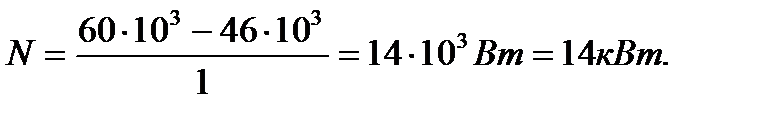
Ответ: 46 кДж, 14 кВт.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2024; Нарушение авторских прав?; Мы поможем в написании вашей работы!