
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. 1) Задача на применение закона Кулона
|
|
|
|
1) Задача на применение закона Кулона.
Два одинаковых маленьких шарика массой по 2г подвешены на шелковых нитях длиной 1м каждая в одной точке. После того как шарикам сообщили одинаковый положительный заряд, они разошлись на расстояние 4см. Определите величину заряда каждого шарика.
Решение:
На каждый шарик действуют три силы: сила тяжести  , сила Кулона , сила Кулона  и сила натяжения нити и сила натяжения нити 
|
Запишем краткое условие задачи.
Дано: СИ
m=2г =2·10-3кг
 =1м
=1м
r=4см =4·10-2м
q-?
| α |
| mg |
| Fк |
| T |
Так как шарики находятся в покое, векторная сумма этих сил равна нулю:  . Это возможно только в том случае, если равнодействующая силы тяжести и силы натяжения нити уравновешивается силой отталкивания:
. Это возможно только в том случае, если равнодействующая силы тяжести и силы натяжения нити уравновешивается силой отталкивания:  . По закону Кулона
. По закону Кулона  . Приравниваем правые части
. Приравниваем правые части  и
и 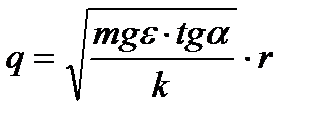 . Угол α найдем, зная, что
. Угол α найдем, зная, что 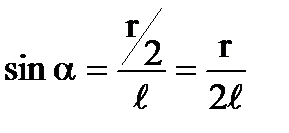 и тогда
и тогда  .
.
Проведем проверку размерности:
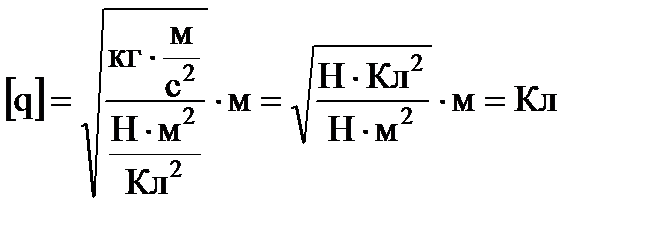
Произведем вычисления:  .
.
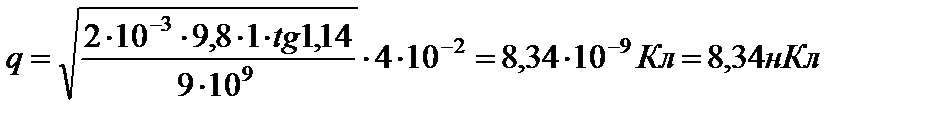 .
.
Ответ: 8,34нКл.
2) Задача на применение принципа суперпозиции.
Два заряда по 20мкКл расположены на расстоянии 6 см друг от друга. Найти напряженность в точке, удаленной на 5см от каждого заряда, если заряды одноименные.
Запишем краткое условие задачи.
Дано: СИ Решение:
q1= 2нКл = 2·10-9Кл
Построим в точке, где ищем напряженность, вектора напряженностей  и и  электрических полей, создаваемых зарядами q1 и q2 с учетом знаков зарядов. электрических полей, создаваемых зарядами q1 и q2 с учетом знаков зарядов.
|
q2= 2нКл = 2·10-9Кл
a= 6см =6·10-2м
b= 5см =5·10-2м
Е-?
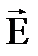
|
| а |
| π-α |
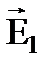
|
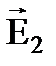
|
| b |
| b |
| α |
По принципу суперпозиции результирующая напряженность 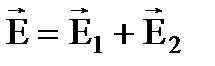 .
.
По теореме косинусов модуль результирующей напряженности  , где
, где
 , так как заряды по модулю равны и равны расстояния от зарядов до точки, в которой ищем результирующую напряженность. α -угол между векторами
, так как заряды по модулю равны и равны расстояния от зарядов до точки, в которой ищем результирующую напряженность. α -угол между векторами  и
и  . Как видно из рисунка этот угол равен углу, лежащему напротив отрезка а в треугольнике, образованном отрезками a, b, b. По теореме косинусов найдем cosα:
. Как видно из рисунка этот угол равен углу, лежащему напротив отрезка а в треугольнике, образованном отрезками a, b, b. По теореме косинусов найдем cosα: 

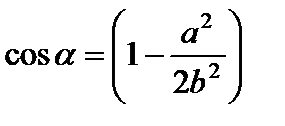 .
.
По формулам приведения  , следовательно
, следовательно

Проведем проверку размерности:

Произведем вычисления:  .
.
Ответ: 11,5 кВ/м.
3) Задача на работу сил электрического поля.
Шарик массой 10-4кг перемещается вдоль силовой линии однородного электрического поля из точки 1 с потенциалом 1000В в точку 2 с потенциалом равным 100В. Определите скорость шарика в точке 1,  если в точке 2 его скорость 20м/с. Заряд шарика 10-5Кл.
если в точке 2 его скорость 20м/с. Заряд шарика 10-5Кл.
Запишем краткое условие задачи.
Решение:
Работа, совершенная силами электрического поля при перемещении заряженного шарика из точки 1 в точку 2, равна изменению его кинетической энергии  : :  , ,  где, где,
|
Дано:
q=10-5Кл
m=10-4кг
φ1=1000В
φ2=100В
v2=20м/с
v1-?
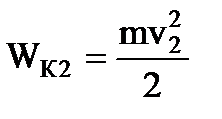 ,
,  -кинетические энергии шарика в точках 2 и 1 соответственно. С другой стороны работу поля можно найти через разность потенциалов:
-кинетические энергии шарика в точках 2 и 1 соответственно. С другой стороны работу поля можно найти через разность потенциалов:  .
.  . Отсюда
. Отсюда 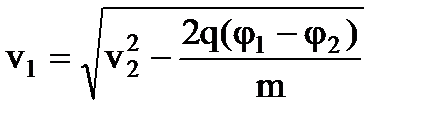 .
.
Проведем проверку размерности:
 =
= 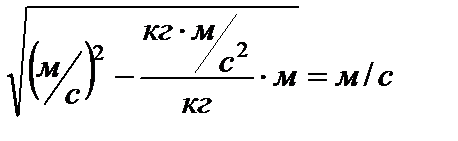
Произведем вычисления: 
Ответ: 14,8м/с
4) Задача на использование формул потенциальной энергии и емкости конденсатора.
Какую работу нужно совершить, чтобы удалить слюдяную пластинку из плоского конденсатора емкостью 10мкФ? Заряд конденсатора 100мкКл.
| Решение: Работа А равна изменению потенциальной энергии конденсатора, взятому со знаком минус: А = -(Wп2 – Wп1) |
Запишем краткое условие задачи.
Дано: СИ
С1=10мкФ =10-5Ф
Q=100мкКл =10-4Кл
А-?
где  - потенциальная энергия конденсатора с пластинкой,
- потенциальная энергия конденсатора с пластинкой, 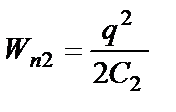 - его потенциальная энергия без пластинки. Заряд конденсатора при удалении пластинки не изменился, так как он отключен от источника тока. Емкость конденсатора с пластинкой
- его потенциальная энергия без пластинки. Заряд конденсатора при удалении пластинки не изменился, так как он отключен от источника тока. Емкость конденсатора с пластинкой  и без нее
и без нее  , ε1, ε2-диэлектрические проницаемости слюды и воздуха соответственно (из таблицы ε1=6, ε2=1). Разделим емкости конденсаторов друг на друга:
, ε1, ε2-диэлектрические проницаемости слюды и воздуха соответственно (из таблицы ε1=6, ε2=1). Разделим емкости конденсаторов друг на друга: 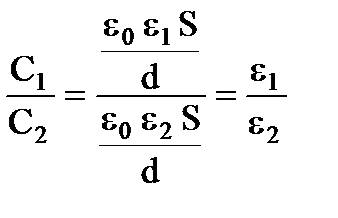 .
.
Отсюда  .
. 
 .
.
И искомая работа:  .
.
Проведем проверку размерности:
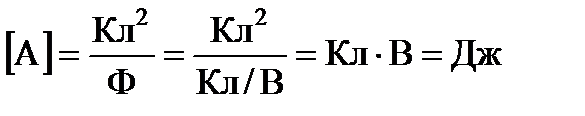
Произведем вычисления: 
Ответ: - 2,5мДж
5) Задача на применение закона Ома.
Лампа подключена медными проводами к источнику тока с ЭДС 2 В и внутренним сопротивление 0,04 Ом. Длина проводов 4 м, их диаметр 0,8 мм. Напряжение на зажимах источника 1,98 В. Найти сопротивление лампы.
Решение:
Напряжение на зажимах источника  , отсюда сила тока в цепи. , отсюда сила тока в цепи.  . Общее сопротивление проводов и лампы . Общее сопротивление проводов и лампы
|
Запишем краткое условие задачи.
Дано: СИ
Е=2В
r=0,05 Ом
 =4м
=4м
d=0,8мм =8·10-4м
Uвн=1,98В
Rл-?
 , где
, где  , ρ-удельное сопротивление меди (из таблицы ρ=1,7·10-8Ом·м),
, ρ-удельное сопротивление меди (из таблицы ρ=1,7·10-8Ом·м), 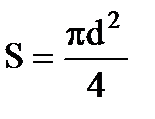 -площадь сечения провода, длина провода удваивается, так как провод двужильный. С другой стороны общее сопротивление цепи по закону Ома для однородного участка цепи:
-площадь сечения провода, длина провода удваивается, так как провод двужильный. С другой стороны общее сопротивление цепи по закону Ома для однородного участка цепи:  .
.
Тогда 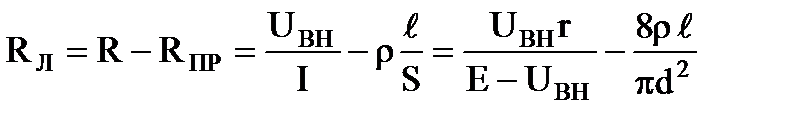 .
.
Проведем проверку размерности:

Произведем вычисления: 
Ответ: 3,33 Ом
6) Задача на определение потерь мощности.
Ток мощностью 2·108Вт необходимо передать на расстояние 200км при напряжении 2·105В. Потери мощности на линии передачи не должны превышать 10%. Какого сечения нужно взять алюминиевый провод?
Решение:
По условию теряемая мощность  . С другой стороны мощность электрического тока, выделяемая на проводнике . С другой стороны мощность электрического тока, выделяемая на проводнике  , отсюда , отсюда 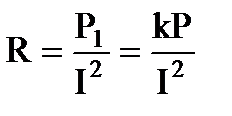 . .
|
Запишем краткое условие задачи.
Дано: СИ
P=2·108Вт
U=2·105В.
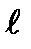 =200км =2·105м
=200км =2·105м
k=0,1
S-?
С учетом того, что ток в цепи 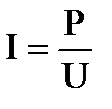 , получим
, получим  . Сопротивление проводов
. Сопротивление проводов 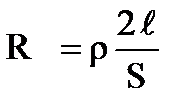 , ρ=2,8·10-8Ом·м – удельное сопротивление алюминия (из таблицы). Приравниваем два выражения для сопротивления
, ρ=2,8·10-8Ом·м – удельное сопротивление алюминия (из таблицы). Приравниваем два выражения для сопротивления 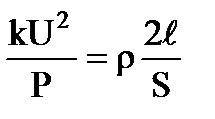

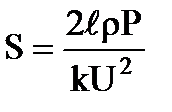 .
.
Проведем проверку размерности:
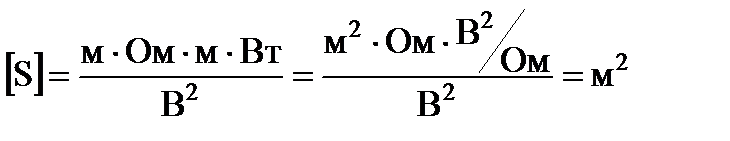
Произведем вычисления:

Ответ: 5,6·10-4 м2.
7) Задача на применение закона Био-Савара-Лапласа.
По квадратной рамке со стороной 0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.
Запишем краткое условие задачи.
| Решение Магнитное поле в центре рамки создается отрезками проводников с током, являющихся сторонами квадрата. |
Дано:
а = 0,2м
I = 4 A
B -? H -?
| I |
| Направления векторов магнитной индукции в центре квадрата найдем по правилу правого буравчика; все они направлены в одну сторону, перпендикулярно плоскости рамки от нас. |
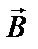
|
| α1 |
| α2 |
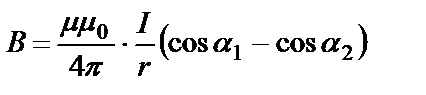 ,
,
здесь r = а/2 – расстояние от проводника до центра квадрата, α1 = 450, α2 = 1350.
Тогда получим расчетную формулу для В:
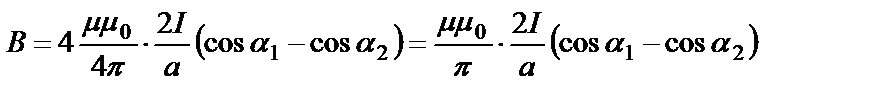
Произведем вычисления:
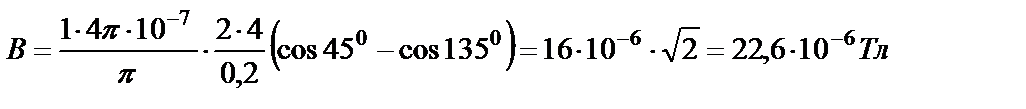
Индукция поля и напряженность связаны соотношением:  .
.
Отсюда 
Ответ: 22,6·10-6 Тл; 18 А/м.
8) Задача на применение закона Ампера.
Прямолинейный проводник массой 2 кг и длиной 59 см помещен в однородное магнитное поле перпендикулярно линиям индукции. Какой ток должен проходить по нему, чтобы он висел не падая? Индукция однородного магнитного поля равна 15 Тл.
Запишем краткое условие задачи.
Решение:
Проводник не будет падать, если сила тяжести  будет уравновешена силой Ампера будет уравновешена силой Ампера 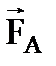 , т.е. модули этих сил , т.е. модули этих сил  . Согласно закону Ампера . Согласно закону Ампера  . .  . Отсюда сила тока . Отсюда сила тока 
|
Дано: СИ
m=2кг
 =59см =0,59м
=59см =0,59м
В=15Тл
α=900
I-?
Проведем проверку размерности:
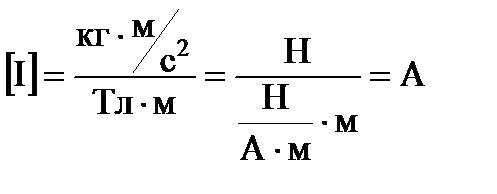 .
.
Произведем вычисления: 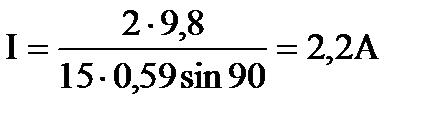 .
.
Ответ: 2,2 А
9) Задача на силу Лоренца.
α-частица, ускоренная разностью потенциалов 250 В, влетает в однородное магнитное поле индукцией 25 мТл, перпендикулярно линиям магнитной индукции и движется по окружности. Найдите радиус окружности и период обращения α-частицы.
Запишем краткое условие задачи.
| Решение: Работа электрического поля затрачивается на увеличение кинетической энергии частицы: |
Дано: СИ
е=1,6·10-19Кл
mp=1,67·10-27кг
U=250B
B=25мТл =25·10-3Тл
α=900.
R, T-?
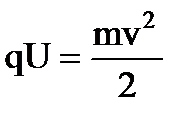

 .
.
В магнитном поле на движущуюся заряженную частицу действует сила Лоренца:  , угол α=900 и
, угол α=900 и  . Согласно второму закону Ньютона
. Согласно второму закону Ньютона 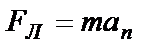 , где
, где  - центростремительное ускорение частицы, движущейся по окружности радиуса R. Получаем
- центростремительное ускорение частицы, движущейся по окружности радиуса R. Получаем  . Окончательно радиус окружности:
. Окончательно радиус окружности:  .
.
Период обращения частицы найдем, разделив длину окружности на скорость частицы:  .
.
Заряд α-частицы: 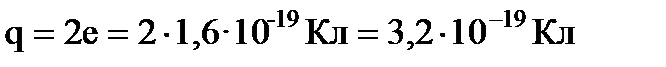 , ее масса
, ее масса 

Проведем проверку размерности:
 =
= 


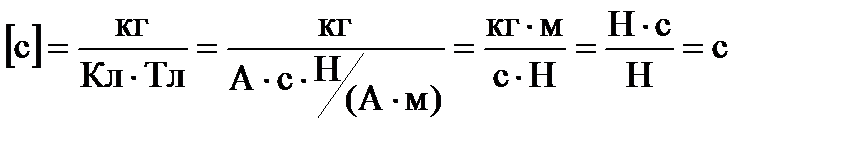
Произведем вычисления: 

Ответ: 0,13 м; 5,2·10-6 с.
10) Задача на электромагнитную индукцию.
Катушка сопротивлением 100 Ом, состоящая из 1000 витков, внесена в однородное магнитное поле, так что линии магнитной индукции параллельны оси катушки. Площадь поперечного сечения катушки равна 5 см2. В течение некоторого времени индукция магнитного поля уменьшилась с 0,09 до 0,04 Тл. Какой заряд индуцирован в проводнике за это время?
Запишем краткое условие задачи.
| Решение: При изменении магнитного потока, пронизывающего катушку в ней возникает индукционный ток силой, по закону Ома равный: |
Дано: СИ
R=100 Ом
N=1000
S=5см2 =5·10-4м2
B1=0,09Тл
B2=0,04Тл
q-?
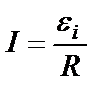 , где
, где 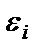 - ЭДС индукции. По определению сила тока
- ЭДС индукции. По определению сила тока 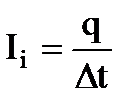 , где
, где 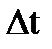 - время протекания заряда через поперечное сечение провода.
- время протекания заряда через поперечное сечение провода.
Приравниваем:  . Отсюда
. Отсюда 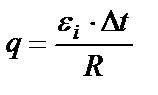 .
.
По закону Фарадея ЭДС индукции, возникающая в катушке содержащей N витков: 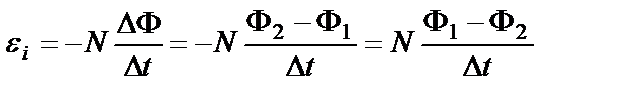 ,
,
где  ,
,  .
.
Угол α между нормалью к плоскости контура и линией магнитной индукции по условию задачи равен нулю, поэтому  .
.
С учетом этого  .
.
Проведем проверку размерности:

Произведем вычисления:  .
.
Ответ: 2,5·10-4 Кл
11) Задача на идеальный колебательный контур.
Колебательный контур состоит из конденсатора емкостью С=5 мкФ и катушки индуктивности L = 0,2 Гн. Определить максимальную силу тока I0 в контуре, если максимальная разность потенциалов на обкладках конденсатора U0 = 90 В. Активным сопротивлением проводов в контуре пренебречь.
Запишем краткое условие задачи.
Решение:
Воспользуемся законом сохранения энергии для идеального колебательного контура:
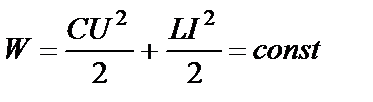
|
Дано: СИ
L=0,2 Гн
С=5 мкФ =5·10-6Ф
U0= 90В
I0 -?
Полная энергия контура равна энергии конденсатора при максимальном значении U:  .
.
Сила тока достигает максимального значения в момент разрядки конденсатора, при этом  .
.
Следовательно,  .
.
Откуда: 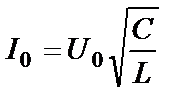 .
.
Произведем вычисления:  .
.
Ответ: 0,45 А
12) Задача на формулу Томсона.
В колебательный контур включен конденсатор емкостью С=0,2 мкФ. Какую индуктивность L нужно включить в контур, чтобы получить в нам электромагнитные колебания частоты υ = 400Гц?
Запишем краткое условие задачи.
Решение:
Воспользуемся формулой Томсона:   .
Циклическая частота равна
ω = 2πυ .
Циклическая частота равна
ω = 2πυ
|
Дано: СИ
С=0,2 мкФ =0,2·10-6Ф
υ= 400Гц
L -?
Следовательно,  .
.
Откуда 
Произведем вычисления: 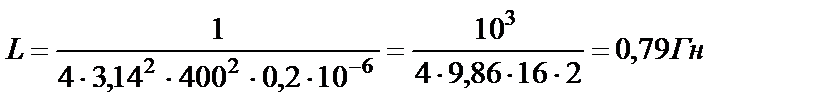 .
.
Ответ: 0,79 Гн.
13) Задача на закон преломления.
На стеклянную пластинку, показатель преломления которой 1,5 падает луч света. Найти угол падения, если угол между отраженным и преломленным лучами 900.
Запишем краткое условие задачи.
| Решение: |
n21 = 1,5
| α |
| φ |
| α =? |
| γ |
Из рисунка видно, что β + φ + γ = 1800. Следовательно, β = 1800 – 900 – γ = 900 – γ.
По закону отражения света α = β = 900 – γ.
Или γ = 900 – α
С другой стороны, по закону преломления света
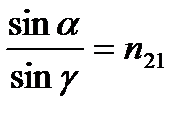 .
.
Таким образом,  .
.
Тогда 
Ответ: 0,98 рад.
14). Задача на явление полного внутреннего отражения.
Луч света выходит из скипидара в воздух. Предельный угол падения для этого луча 42023'. Определить скорость распространения света в скипидаре.
Запишем краткое условие задачи.
| Решение: Показатели преломления скипидара n1 и воздуха n2 связаны со скоростями распространения света |
αпр = 42023'
с = 3∙108 м/с
| Vск=? |
в этих средах соотношением:
 .
.
Предельный угол падения находится из условия
 .
.
Следовательно,
 ,
,
а искомая скорость  .
.
Ответ: 2,02∙108 м/с.
15) Задача на формулу линзы.
Собирающая линза дает действительное увеличенное в два раза изображение предмета. Определить фокусное расстояние линзы, если расстояние между линзой и изображением предмета 24 см.
Запишем краткое условие задачи.
| Решение: Для нахождения фокусного расстояния воспользуемся формулой линзы: |
| СИ 0,24 м |
k = 2
f = 24 см
| F=? |
.
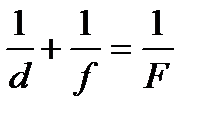
Выразим из нее F:
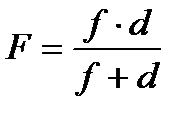 .
.
Так как линейное увеличение линзы
 , то
, то  .
.
Подставив полученное значение d в формулу для F, получим:
 .
.
Проведем вычисления:

Ответ: 0,08 м.
16) Задача на интерференцию света.
В некоторую точку пространства приходят две когерентные волны с оптической разностью хода1,8 мкм. Определить, усилится или ослабится свет в этой точке, если длина волны 600 нм.
| Решение: В точке наблюдения свет усилится, если оптическая разность хода равна целому числу длин волн. |
| СИ 6∙10-7 м 1,8∙10-6 м |
Дано:
λ = 600 нм
Δ = 1,8 мкм
Проверим это:
 .
.
Следовательно, в точке наблюдения свет усилится.
Ответ: интерференционный максимум.
17) Задача на дифракционную решетку.
Найти наибольший порядок спектра для желтой линии натрия с длиной волны 5890 А0, если период дифракционной решетки 2 мкм.
| Решение: Запишем формулу для дифракционной решетки: d·sinα = m·λ |
| СИ 5,89∙10-7 м 2∙10-6 м |
Дано:
λ = 5890 А0
d = 2 мкм
m-?
Выразим  , порядок спектра m принимает наибольшее значение при максимальном значении sinα = 1, но так как порядок спектра – это целое число, то нужно найти целую часть дроби
, порядок спектра m принимает наибольшее значение при максимальном значении sinα = 1, но так как порядок спектра – это целое число, то нужно найти целую часть дроби 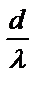 .
.
Проведем вычисления:

Следовательно, m = 3
Ответ: 3
18) Задача на фотоэффект.
Определить наибольшую скорость электрона, вылетевшего из пластинки цезия, при освещении ее светом с длиной волны 400 нм.
Запишем краткое условие задачи.
| Решение: Для решения задачи запишем формулу Эйнштейна для фотоэффекта. |
| СИ 4∙10-7 м |
Дано:
λ0 = 400 нм
Vmax=?

Работу выхода для цезия найдем по справочнику Авых = 3,2 ·10-19 Дж.
Из формулы Эйнштейна выразим искомую скорость:
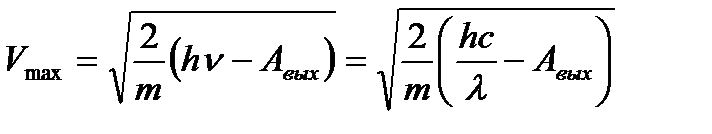 .
.
Проведем вычисления:
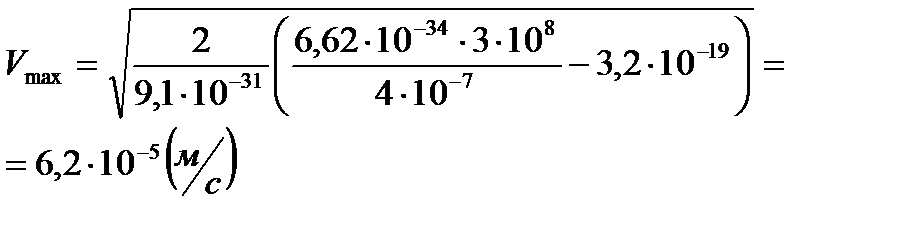
Ответ: 6,2 ·10-5 м/с.
19) Задача на тепловое излучение.
Максимум энергии излучения черного тела при некоторой температуре приходится на длину волны λm = 1 мкм. Вычислить испускательную способность тела при этой температуре и энергию W, излучаемую с площади S = 300 см2 поверхности тела за время t = 1 мин. Определить также массу, соответствующую этой энергии.
Запишем краткое условие задачи.
| R0 -? m -? W -? |
| λm = 1 мкм S = 300 см2 t = 1 мин |
| 1∙10-6 м 3∙10-2 м2 60 с |
Интегральная лучеиспускательная способность абсолютно черного тела определяется из закона Стефана-Больцмана:
R0 = σT4, (1)
где σ – постоянная Стефана-Больцмана; σ = 5,67∙10-8 Вт/(м2∙К4); T – термодинамическая температура тела. Из закона смещения Вина λm =b/T
определим термодинамическую температуру:
T = b/ λm, (2)
где λm – длина волны, на которую приходится максимум излучения при температуре Т; b – постоянная Вина; b = 2,89∙10-3 м∙К.
Подставив выражение для Т из (2) в (1), получим:
R0 = σ(b/ λm)4. (3)
Энергию, излучаемую с площади S поверхности тела за время t, определим по формуле:
W = R0St. (4)
По закону Эйнштейна взаимосвязи энергии и массы
W = mc2,
(с – скорость света в вакууме; с = 3∙108 м/с; W – энергия) найдем массу, соответствующую энергии излучения:
m = W/c2. (5)
Проведем проверку размерности:
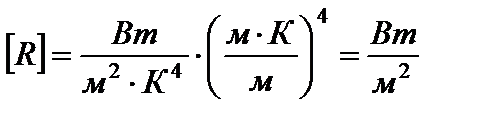 .
.
Произведем вычисления:

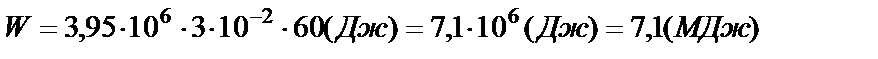 ;
;

Ответ: R0 =  ; W=
; W= 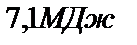 ; m =
; m =  .
.
20) Задача по атомной физике.
Определить энергию фотона, излучаемого атомом водорода при переходе электрона с третьего энергетического уровня на первый, а также длину электромагнитной волны, соответствующую этому фотону.
Запишем краткое условие задачи.
| n = 1 k = 3 |
| E -? λ -? |
W = hν = hc/λ,
где W – энергия фотона; h – постоянная Планка; h = 6,625∙10-34 Дж∙с; с – скорость света в вакууме, ν, λ – частота и длина волны, соответствующие фотону с энергией W.
Длина волны излучаемого света определяется по формуле Бальмера-Ридберга:
 ,
,
где R – постоянная Ридберга; R = 1,10∙107 м-1; n – номер энергетического уровня, на который переходит электрон; k - номер энергетического уровня, с которого уходит электрон.
Произведем вычисления:
 ,
,
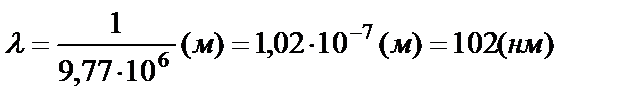 .
.

Ответ: λ = 102 нм; W = 12,2 эВ.
21) Задача по ядерной физике.
Определить дефект массы Δm, энергию связи Wсв и удельную энергию связи ядра атома бора  .
.
Решение:
Дефект массы ядра представляет собой разность массы нуклонов (протонов и нейтронов), составляющих ядро, и массы ядра и определяется по формуле:
Δm = Zmp + (A – Z)mn – mя, (1)
где Z – зарядовое число (число протонов в ядре); mp – масса протона; А – массовое число (общее число нуклонов в ядре); (A – Z) – число нейтронов в ядре; mn – масса нейтрона; mя – масса ядра.
Числа Z и А указываются при написании символа элемента: Z – слева внизу; А – слева вверху; в данном случае для бора Z = 5, А = 10. Массу ядра найдем по формуле
mя = mа – Z∙me, (2)
где mа – масса нейтрального атома; me – масса электрона.
Чтобы не вычислять каждый раз массу ядра, преобразуем формулу (1) с учетом (2):
Δm = Zmp + (A – Z)mn – mа (3)
Из таблицы данных выпишем: mp = 1,00783 а.е.м., mn = 1,00867 а.е.м., mа = 10,01294 а.е.м..
Подставим числовые значения величин, входящих в (3), и вычислим дефект массы ядра бора:
Δm=5∙1,00783 а.е.м. + (10-5)∙1,00867 а.е.м. − 10,01294 а.е.м. = 0,06956 а.е.м.
Энергия связи ядра – энергия, выделяющаяся при образовании ядра в виде электромагнитного излучения, определяется по формуле:
Wсв = Δmс2, (4)
где с – скорость света в вакууме, с = 3∙108 м/с.
Если энергию связи выразить в мегаэлектрон-вольтах, дефект массы Δm ядра – в атомных единицах массы, то формула (4) примет вид:
Wсв = 931∙ Δm, (5)
где 931 – коэффициент, показывающий, какая энергия в мегаэлектрон-вольтах соответствует массе 1 а.е.м.. Подставив значение Δm в (5), вычислим энергию связи:
Wсв = 931∙ 0,06956 (МэВ) = 64,8 (МэВ).
Удельная энергия связи – это энергия связи, приходящаяся на 1 нуклон в ядре, она равна: 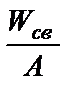 .
.
Произведем вычисления:

Ответ: Δm = 0,06956 а.е.м.; Wсв = 64,8 МэВ;  .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1978; Нарушение авторских прав?; Мы поможем в написании вашей работы!