Моделирование как метод познания

Моделирование. Человечество в своей деятельности постоянно создает и использует модели окружающего мира. Строгие правила построения моделей сформулировать невозможно, однако человечество накопило богатый опыт моделирования различных объектов и процессов.

Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы и др.). Наглядные модели часто используются в процессе обучения. В курсе географии первые представления о нашей Земле мы получаем, изучая ее модель – глобус.

Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов и т.д. Без предварительного создания чертежа невозможно изготовить даже простую деталь.

Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез и т.д), отражающих строение, свойства и поведение реальных объектов.

Все художественное творчество фактически является процессом создания моделей. Любое литературное произведение может рассматриваться как модель реальной человеческой жизни.

! Моделирование – это метод познания, состоящий в создании и исследовании моделей.

Модель. Каждый объект имеет большое количество различных свойств. В процессе построения модели выделяются главные, наиболее существенные для проводимого исследования свойства.

Разные науки исследуют модели и процессы под разными углами зрения и строят различные типы моделей. В физике изучаются процессы взаимодействия и изменения объектов, в химии – их химический состав, в биологии – строение и поведение живых организмов т.д.

! Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.

Один и тот же объект может иметь разные модели. Например, различные типы географических карт (политические, физические и др.). С другой стороны, разные объекты могут описываться одной моделью. Так в механике различные материальные тела (от планеты до песчинки) могут рассматриваться как материальные точки.

! Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью.

Никакая модель не может заменить сам объект. Но при решении конкретной задачи, когда нас интересуют определенные свойства изучаемого объекта, модель оказывается полезным, а подчас и единственным инструментом исследования.

1. Формы представления моделей. Формализация.

Модели материальные и информационные. Все модели можно разбить на два класса.

Модели

Предметные Информационные

Предметные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме (глобус, анатомические муляжи и др.).

Информационные модели представляют объекты и процессы в образной или знаковой форме. Образные модели (рисунки, фото и т.д.) представляют собой зрительные образы объектов, зафиксированные на каком – либо носителе информации. Знаковые модели строятся с использованием различных языков. Знаковая информационная модель может быть представлена в форме текста, формулы, таблицы и т.д.

Формализация. С помощью формальных языков строятся формальные информационные модели (математические, логические и др.). Одним из наиболее широко используемых формальных языков является математика. Модели, построенные с использованием математических понятий и формул, называются математическими моделями.

! Процесс построения информационных моделей с помощью формальных языков называется формализацией.

1. Этапы решения задач на компьютере.

Этапы решения задач на компьютере:

		Составление программы на языке программирования		Анализ полученных результатов и корректировка исследуемой модели
		Формализованная модель задачи
	Содержательная постановка задачи			Составление алгоритма решения задачи

Содержательная постановка задачи – это формулировка задачи, излагаемая в терминах некоторой конкретной области науки, техники и т.д. Суть этого этапа в том, что здесь четко формулируется: что дано? что найти? как найти?. Выделяются исходные данные и результаты.

Формализованная (математическая) модель задачи – это формулировказадачи, как задачи некоторого раздела математики. Фактически рассматриваются те же вопросы, что и в содержательной постановке задачи, но сформулированные на языке математики. Переход к математической задаче дает возможность подобрать и применить для ее решения методы, разработанные математикой.

Составление алгоритма решения задачи – данный этап, а так же два последующие будут рассмотрены в следующих разделах.

1. Исследование моделей.

Исследование математических моделей. Исследование математических моделей начинается с записи формальной модели на языке определенной области математики: алгебры, геометрии и т.д.

Приближенное решение уравнений. На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы. Точные решения существуют только для некоторых уравнений, поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические, числовые и др.).

Графический метод. Построение графиков функций может использоваться для грубо приближенного решения уравнений. Рассмотрим уравнение вида:

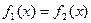, где

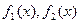- некоторые непрерывные функции, корень (или корни) уравнения являются точкой пересечения (или точками) графиков этих функций.

Задача. Найти графическим методом корень уравнения .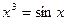

Формальная модель задачи задана уравнением. Решать задачу будем с использованием средств MS Excel.

Исследование биологических моделей. В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб и т.д.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник – жертва».

Модель неограниченного роста. Это простейшая модель в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно записать с помощью формулы:

, где

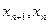- численность популяции следующего года и текущего года, а - коэффициент роста.

Модель ограниченного роста. В данной модели учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и т.д., который замедляет рост популяции с увеличением ее численности. Математическую модель можно записать с помощью формулы:

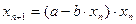, где

b - коэффициент перенаселенности (b<a).

Модель «хищник-жертва». Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом является взаимодействие между жертвами и хищниками (караси – щуки, зайцы – волки и т.д.). В модели хищник-жертва количество жертв 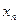и количество хищников 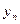связаны между собой. Формула для расчета численности жертв принимает вид:

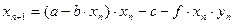, где

f- коэффициент, который характеризуетвозможность гибели жертвы при встрече с хищником,

с- величина ежегодного отлова жертв.

Численность популяции хищников в отсутствии жертв (в связи с отсутствием пищи) уменьшается, что можно описать рекурретной формулой:

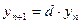, где

d<1 - характеризует скорость уменьшения численности популяции хищников.

Численность популяции хищников при наличие жертв (пищи) описывается формулой:

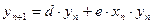, где

е – коэффициент, характеризующий величину роста численности хищников за счет жертв.

Задания для самостоятельного выполнения.

Для приведенных задач выполнить математическую постановку:

1. Даны сведения о количестве осадков, выпавших в каждый день месяца. Определить общее количество осадков за месяц

2. Вычислить площадь треугольника по заданным сторонам а, в, с.

3. Определить средний рост учеников одного класса, если задан рост каждого ученика.

4. Вычислить объем шара, если известен его радиус R.

5. Какие существуют варианты размена купюры достоинством N руб. купюрами 100, 200, 500 рублей?

6. Выполнить начисление зарплаты согласно следующему правилу:

- если стаж работы сотрудника менее 5 лет, зарплата начисляется в размере 15 тыс. руб.;

- при стаже работы от 5 до 15 лет - 20 тыс. руб.;

- при стаже свыше 15 лет зарплата повышается с каждым годом на 2тыс. руб.

Раздел IV. Основы алгоритмизации.

1. Алгоритм и его формальное исполнение.

Понятие алгоритма. Алгоритмом называется четко сформулированный, предельно понятный порядок операций для решения той или иной задачи. Но описание этого метода следует выполнять в соответствии с определенными правилами, а именно:

ü Выделить величины, являющиеся исходными для задачи.

ü Разбить процесс решения задачи на такие этапы, которые известны исполнителю и которые он может выполнить однозначно без всяких пояснений.

ü Указать порядок выполнения этапов.

ü Указать признак окончания процесса решения задачи.

ü Указать во всех случаях, что является результатом решения задачи.

Составить такое описание обычно нелегко, но, следуя ему, механически выполняя все указанные в нем этапы в требуемом порядке, исполнитель всегда правильно решит задачу. Дадим строгое определение данному понятию.

! Алгоритм – это метод (способ) решения задачи, записанный по определенным правилам, обеспечивающим однозначность его понимания и механического исполнения при всех значениях исходных данных (из некоторого множества значений).

Пример алгоритма может служить любой кулинарный рецепт.

Выделим и раскроем основные свойства алгоритма.

Свойства алгоритма:

Ø Дискретность алгоритма. Процесс решения задачи расчленен на отдельные элементарные действия (шаги) и соответственно алгоритм представляет последовательность указаний, команд, определяющих порядок выполнения шагов.

Ø Определенность алгоритма. Каждая команда алгоритма должна быть понятна исполнителю, не оставлять места для ее неоднозначного толкования и неопределенного исполнения.

Ø Результативность алгоритма. Алгоритм всегда приводит к результату через конечное число шагов.

Ø Массовость алгоритма. Каждый алгоритм, разработанный для решения некоторой задачи, должен быть применим для решения задачи этого типа при всех допустимых значениях исходного типа

Исполнение алгоритма должно привести к решению соответствующей задачи, получению результата. Суть процесса исполнения в педантичном выполнении операций алгоритма в требуемом порядке.

1. Способы описания алгоритмов.

В настоящее время используется несколько таких способов.

1. Словесно-формульное описание алгоритма – описание алгоритма с помощью слов и формул. Рассмотрим пример такого описания.

Задача 2.1. Составить алгоритм начисления зарплаты согласно следующему правилу:

если стаж сотрудника менее 5 лет, то зарплата – 15 тыс. руб.,

при стаже работы от 5 до 15 лет - зарплата 18 тыс. руб.,

при стаже свыше 15 лет зарплата повышается с каждым годом на 2 тыс. руб..

Сформулируем задачу в математическом виде (формальная модель): вычислить значение функции:

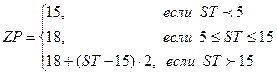
где ZP – зарплата; ST – стаж работы.

Словесно-формульное описание алгоритма решения задачи 2.1:

1. Ввести ST, перейти к п. 2.

2. Если ST < 5, то ZP:=15, перейтик п.4, иначе – перейти к п. 3.

3. Если ST ≤15, то ZP:=18, перейти к п. 4, иначе ZP:=18+(ST-15)∙2, перейти к п. 4.

4. Вывести значение ZP, перейти к п. 5.

5. Вычисления прекратить.

2.Графическое описание алгоритма – описание с помощью схем алгоритмов. Схема алгоритма представляет собой систему связанных геометрических фигур. Каждая фигура обозначает один этап процесса решения задачи и называется блоком. Порядок выполнения этапов указывается стрелками, соединяющими блоки.

Операция присваивания изображается прямоугольником:

- Блок «Процесс»

Операции Ввод и Вывод изображаются параллелограммом:

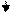
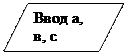
- Блок «Ввод» - Блок «Вывод»

Операция Условный переход изображается ромбом, блок имеет два выхода - Да и Нет:

Да х<7 Нет

Если условие выполняется выходим из блока по выходу Да, если не выполняется – по выходу Нет.

Начало процесса решения задачи обозначается блоком Начало.

Завершение процесса решения задачи обозначается блоком Останов.

Последние два блока изображаются так:

Можно сформулировать общие правила построения схемы алгоритма задачи

• Выявить исходные данные, результаты, назначить им имена.
• Выбрать метод (порядок) решения задачи.
• Разбить метод решения задачи на этапы (с учетом возможностей ЭВМ).
• Изобразить каждый этап в виде соответствующего блока-схемы алгоритма и указать стрелками порядок их выполнения.
• В полученной схеме при любом варианте вычислений предусмотреть выдачу результатов или сообщений об их отсутствии, обеспечить возможность перейти к блоку Останов.

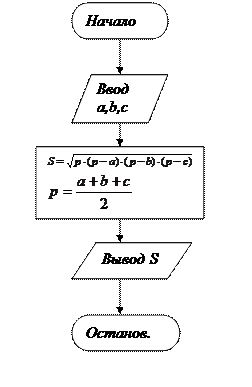
Задача 2.2. Составить алгоритм вычисления площади треугольника по трем сторонам.

Решение. Составим математическую модель задачи, то есть запишем необходимые формулы.

Для вычисления площади треугольника воспользуемся формулой:

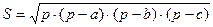, где

a, b, c- стороны треугольника (исходные данные),

p – полупериметр треугольника (),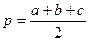

S – результат.

Решение задачи распадается на четыре этапа. Изображаем каждый этап в виде определенной геометрической фигуры (блока) и соединяем их стрелками. В результате получаем схему алгоритма задачи:

Задания для самостоятельного выполнения.

Составить алгоритмы решения задач, описать их с помощью схемы.

1. Определить средний рост учеников одного класса, если задан рост каждого ученика. В классе 15 учеников.

2. Вычислить объем шара, если известен его радиус R.

3. Какие существуют варианты размена купюры достоинством N руб.купюрами 100, 200, 500 рублей?

4. Вычислить значение функции

.

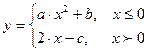1. Виды алгоритмов.

Линейные алгоритмы. Линейным называется алгоритм в котором все этапы решения задачи выполняются строго последовательно.

Пример линейного алгоритма – это схема алгоритма задачи 2.2.

Структура такого алгоритма показана на рисунке:

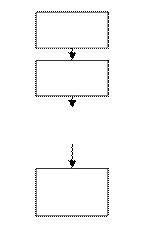
Разветвляющиеся алгоритмы. Разветвляющимся называется такой алгоритм, в котором выбирается один из нескольких возможных путей (вариантов) вычислительного процесса. Каждый путь называется ветвью алгоритма. Примером такого алгоритма является алгоритм решения задачи 2.1.

Признаком разветвляющегося алгоритма является наличие операций проверки условия (в схеме присутствует логический блок).

Дата добавления: 2014-12-27