Формулы для расчета характеристик рядов распределения

Методические рекомендации

Основные формулы для расчета характеристик рядов распределение приведено в табл. 5.1.

Табл. 5.1

Характеристики рядов распределения	Формулы расчета
Мода
Медиана
Дисперсия
Среднее квадратичное отклонение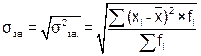
Коэффициент вариации

Решить задачи анализа рядов распределения в табличном процессоре Excel можно благодаря использованию программной надстройки Пакет анализа и встроенных статистических функций. Рассмотрим порядок работы в Excel.

Анализ несгруппированных статистических данных. Работа начинается с запуска Excel (аналогично запуска других прикладных программ – через меню ПУСК или используя ярлык). При формировании файла с данными показатели не обязательно вводить во входную таблицу табличного процессора, их можно перенести из документов Microsoft Office через буфер обмена. После чего, если нужно, происходит преобразование и визуализация первичных данных (рис. 5.1).

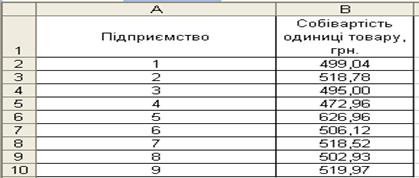
Рис. 5.1. Входные данные

Режим Описательная статистика служит для генерации одномерного статистического отчета за основными показателями положения, рассеивания и асимметрии совокупности, которая анализируется. Для перехода в этот режим необходимо войти в позицию меню Сервис – Анализ данных и избрать данный режим (рис. 5.2).

Рис. 5.2. Избрание режима Описательная статистика

В диалоговом окне данного режима (рис. 5.3) задаются такие параметры:

1. Входной интервал – вводится ссылка на ячейки, которые содержат статистические данные.

2. Группировка – устанавливается у положение По столбцах или По строкам в зависимости от расположения данных во входном диапазоне.

3. Метки в первой строке – активизируется, если первая строка (столбец) во входном диапазоне содержит заголовки. Если заголовки отсутствуют, необходимо деактивировать эту функцию. В этом случае будут автоматически созданные стандартные названия для данных исходного диапазона;

4. Исходный интервал/ Новый рабочий лист/ Новая рабочая книга. В положении Исходный интервал активизируется поле, в которое необходимо ввести ссылку на левую верхнюю клеточку исходного диапазона. Размер исходного диапазона будет определен автоматически, и на экране появится сообщение в случае возможного наложения исходного диапазона на входные данные. В положении Новый рабочий лист приоткрывается новое письмо, в которое начиная с ячейки А1 устанавливаются результаты анализа. Если нужно задать имя новому рабочему листу, которое приоткрывается, введите его имя в поле, расположенное напротив.

В положении Новая рабочая книга приоткрывается новая книга, на первом листе которой начиная из клеточки А1 вставляют результаты анализа;

5. Итоговая статистика – активизируется, если в исходном диапазоне необходимо получить по одному полю для каждого показателя описательной статистики.

6. Уровень надежности – активизируется, если в исходную таблицу необходимо включить строку для предельной погрешности выборки при установленном уровне надежности.

7. К-й наибольший – активизируется, если в исходную таблицу необходимо включить строку для к -го наибольшего (начиная с максимума х_max) значение элемента совокупности. В поле напротив введите число к. Если к = 1, то строка будет содержать максимальное значение элемента выборки.

8. К-й наименьший – активизируется, если в исходную таблицу необходимо включить строку для к -го наименьшего (начиная с х_min) значение элемента выборки. В поле напротив введите число к. Если к = 1, то строка будет содержать минимальное значение элемента выборки.

Введенные параметры режима Описательная статистика представлены на рис. 5.3, а рассчитанные показатели в данном режиме - на рис. 5.4.

Рис. 5.3. Значение параметров режима Описательная статистика

Рис. 5.4. Рассчитанные показатели описательной статистики

Согласно полученным данным: коэффициент осцилляции

коэффициент вариации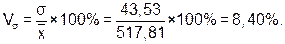

Анализ сгруппированных статистических данных. После ввода или перенесение из документов Microsoft Office через буфер обмена входных данных в таблицу Excel, если нужно, происходит преобразование и визуализация первичных данных. В данном случае, необходимо прибавить столбец с индивидуальными значениями усредняемого признака (середину интервала) по каждой группе (рис. 5.5).

В явном виде функция для расчета средней арифметической взвешенной не представлена в Excel. Но ее возможно получить комбинацией других функций.

Ячейка С9 содержит формулу =СУММПРОИЗВ(C3:C8;B3:B8)/ СУММ(B3:B8), благодаря которой рассчитывается средняя сумма оборотных активов (рис. 5.5).

Для определения моды и медианы необходимо провести некоторые расчеты (рис. 5.6 и 5.7).

Расчет моды ряд представлен на рис. 5.6.

Рис. 5.5. Расчет средней суммы оборотных активов

Рис. 5.6. Расчет моды ряда

Содержание ячеек рис. 5.6:

ячейка С9 содержит формулу =МАКС(B3:B8) - рассчитывается модальное количество предприятий;

ячейка С10 содержит формулу =ПОИСКПОЗ(C9;B3:B8;0) - в массиве B3:B8 рассчитывается смещение на модальное значение;

ячейка С11 содержит формулу =ИНДЕКС(A3:A8;C10;1) - в массиве A3:A8 находится модальный интервал суммы оборотных активов;

ячейка С12 содержит формулу =ЛЕВСИМВ(C11;1) - отображается нижняя граница модального интервала суммы оборотных активов;

ячейка С13 содержит формулу =ИНДЕКС(B3:B8;C10-1;1) – в массиве B3:B8 находится количество предприятий, которые имеют меньшую сумму оборотных активов ();

ячейка С14 содержит формулу =ИНДЕКС(B3:B8;C10+1;1) – в массиве B3:B8 находится количество предприятий, которые имеют большую сумму оборотных активов ();

ячейка С15 содержит формулу =C12+2?((C9-C13)/((C9-C13)+(C9-C14))) - рассчитывается мода суммы оборотных активов.

В связи с тем, что медиана делит численность ряда пополам, то она будет там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности (рис. 5.7).

Рис. 5.7. Расчет медианы ряда

Содержание клеточек рис. 5.7:

в ячейках С3:С8 рассчитывается накопленная частота (например, ячейка С5 содержит формулу =C4+B5);

ячейка В9 содержит формулу =СУММ(B3:B8) - рассчитывается численность совокупности (количество предприятий);

ячейка С10 содержит формулу =B9/2 - определяется половина численности совокупности (50 % количества предприятий);

ячейка С11 содержит формулу =ПОИСКПОЗ(C10;C3:C8;1) - в массиве С3:С8 определяется номер позиции числа, которое есть наибольшим среди чисел меньших или равных середине интервала, т.е. числа 99;

ячейка С12 содержит формулу =ИНДЕКС(C3:C8;C11;1) - из массива С3:С8 берется число, которое удовлетворяет условиям поиска, сформированным в клеточке С11;

ячейка С13 содержит формулу =ЕСЛИ(C10=C12;C11;C11+1) - рассчитывается смещение на медианный интервал;

ячейка С14 содержит формулу =ИНДЕКС(B3:B8;C13;1) - отображается значение частоты медианного интервала;

ячейка С15 содержит формулу =ИНДЕКС(A3:A8;C13;1) - в массиве А3:А8 находится медианный интервал;

ячейка С16 содержит формулу =ЛЕВСИМВ(C15;1) - отображается нижняя граница медианного интервала;

ячейка С17 содержит формулу =ИНДЕКС(C3:C8;C13-1;1) - находится значение накопленной частоты предмедианного интервала;

ячейка С18 содержит формулу =C16+2?((B9/2-C17)/C14) - рассчитывается медиана суммы оборотных активов.

Расчет среднего квадратичного отклонения разрешил определить коэффициент вариации (рис. 5.8).

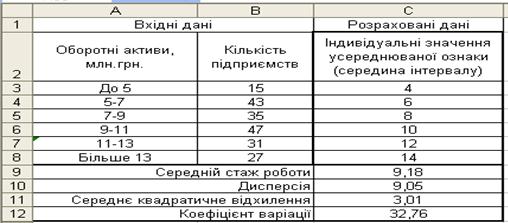
Рис. 5.8. Расчет дисперсии, среднего квадратичного отклонения и коэффициента вариации

Определение этих показателей (рис. 5.8) осуществлено с помощью таких формул:

ячейка С10 содержит =(СУММПРОИЗВ(СТЕПЕНЬ(C3:C8-C9;2);B3:B8))/СУММ(B3:B8) - расчет дисперсии;

ячейка С11 содержит =КОРЕНЬ(C10) - расчет среднего квадратичного отклонения;

ячейка С12 содержит =(C11/C9)?100 - расчет коэффициента вариации.

Для расчета квартильного показателя вариации необходимо сначала определить верхний и нижний квартили.

Вычисление первого квартиля (рис. 5.9) выполняется аналогично расчета медианы, кроме таких клеточек:

ячейка С10 содержит формулу =B9×0,25;

ячейка С18 содержит формулу =C16+2× ((B9×0,25-C17)/C14).

Рис. 5.9. Расчет первого квартиля

Третий квартиль находится в интервале 11-13 лет и равняется 11,5. Для его определения ячейка В10 содержит формулу =B9×0,75, а В18 - формулу =C16+2?((B9?0,75-C17)/C14).

Таким образом, квартильное отклонение равняется

а квартильний показатель вариации -

Результаты расчета общей дисперсии и ее составных представлено на рис. 5.10.

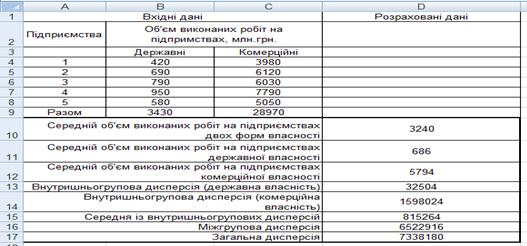
Рис. 5.10. Расчет общей дисперсии и ее составных

Содержание ячеек рис. 5.10:

ячейка D10 содержит формулу =(B9+C9)/(5+5) - расчет среднего объема выполненных работ на предприятиях двух форм собственности;

ячейка D11 содержит формулу =B9/5 - расчет среднего объема выполненных работ на предприятиях государственной собственности;

ячейка D12 содержит формулу =C9/5 - расчет среднего объема выполненных работ на предприятиях коммерческой собственности;

ячейка D13 содержит формулу =ДИСПР(B4:B8) - расчет внутригрупповой дисперсии (государственная собственность);

ячейка D14 содержит формулу =ДИСПР(C4:C8) - расчет внутригрупповой дисперсии (коммерческая собственность);

ячейка D15 содержит формулу =(D13×5+D14×5)/10 - расчет средней из внутригрупповых дисперсий;

ячейка D16 содержит формулу =((СТЕПЕНЬ(D11-D10;2)) × 5+(СТЕПЕНЬ(D12-D10;2)) ×5)/10 - расчет межгрупповой дисперсии;

ячейка D17 содержит формулу =СУММ(D15;D16) - расчет общей дисперсии.

Полученые дисперсия та среднее квадратичное отклонение альтернативный признак представлен на рис. 5.11.

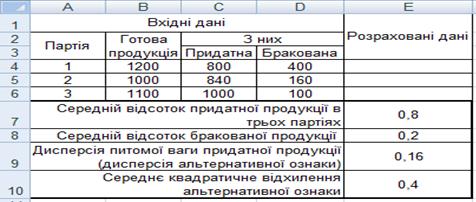
Рис. 5.11. Расчет дисперсии и среднего квадратичного
отклонения

Определение этих показателей (рис. 5.11) осуществлено с помощью таких формул:

ячейка Е7 содержит =(СУММ(C4:C6))/СУММ(B4:B6) - расчет среднего процента годной продукции в трех партиях;

ячейка Е8 содержит =1-E7 - расчет среднего процента бракованной продукции;

ячейка Е9 содержит =E7?E8 - расчет дисперсии удельного веса годной продукции (дисперсии альтернативного признака);

ячейка Е10 содержит =КОРЕНЬ(E9) - расчет среднего квадратичного отклонения альтернативного признака.

Определение коэффициентов асимметрии и эксцесса предусматривает расчет моментов третьего и четвертого порядков (рис. 5.12).

Содержание клеточек ри. 5.12:

ячейка С11 содержит =(СУММПРОИЗВ(СТЕПЕНЬ(C3:C8-C9;3);B3:B8))/СУММ(B3:B8) - расчет момента третьего порядка;

ячейка С12 содержит =C11/СТЕПЕНЬ(C10;3) - расчет коэффициента асимметрии;

ячейка С13 содержит =(СУММПРОИЗВ(СТЕПЕНЬ(C3:C8-C9;4);B3:B8))/СУММ(B3:B8) - расчет момента четвертого порядка;

ячейка С14 содержит =(C13/СТЕПЕНЬ(C10;4))-3 - расчет коэффициента эксцесса.

Рис. 5.12. Расчет коэффициентов асимметрии и эксцесса

Дата добавления: 2014-12-23